Презентация на тему Смежные и вертикальные углы

Решение задач
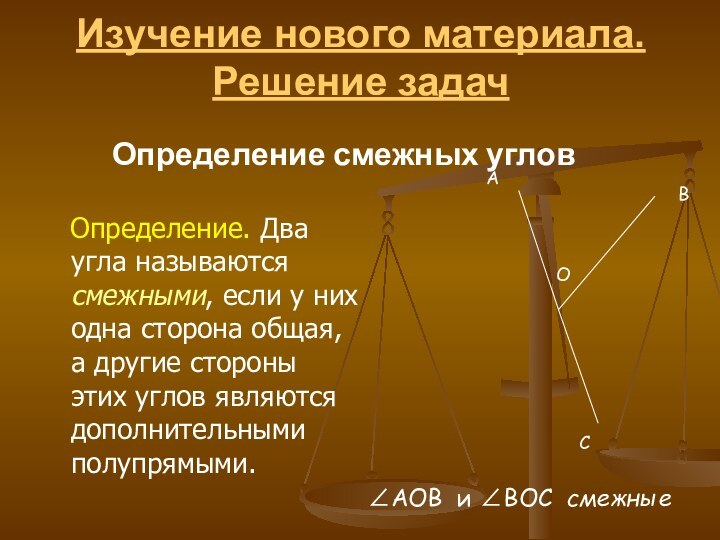
Определение смежных углов
Построение смежных углов
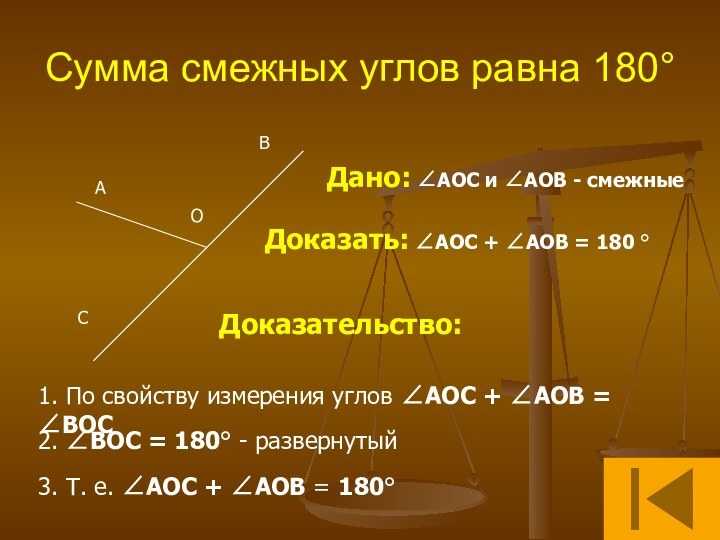
Свойство смежных углов
Пример оформления

задачи
Вертикальные углы
Свойство вертикальных углов
Пример оформления задачи
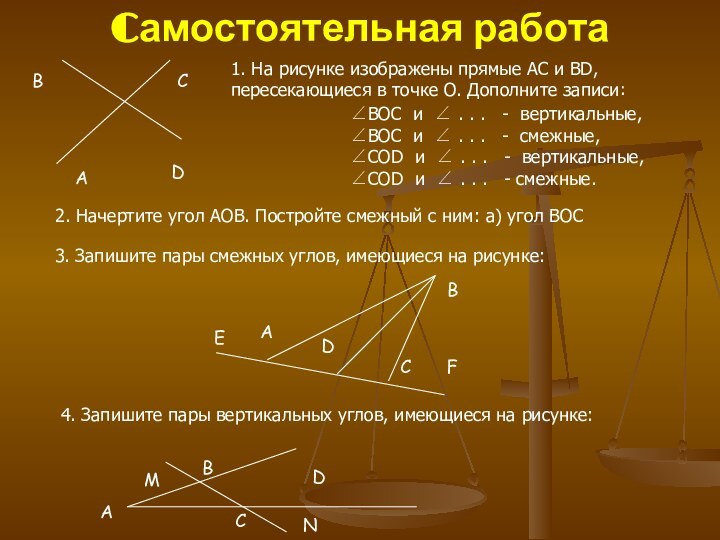
4. Закрепление: самостоятельная работа4. Закрепление: самостоятельная работа
5. Домашнее задание

их свойства
развивать умение сравнивать, выявлять закономерности, обобщать
воспитывать

потребность в доказательных рассуждениях
воспитывать аккуратность при выполнении рисунков
ответственное отношение к учебному труду

такое вершина и стороны угла?
Какой угол называется развернутым?

Единицы измерения угла.

угла называются смежными, если у них одна сторона общая,

а другие стороны этих углов являются дополнительными полупрямыми.

Определение смежных углов

∠AOB и ∠ВОС смежные

смежные

Какие это углы?
2. Существует ли какая-нибудь взаимосвязь между этими

углами? (Вспомните свойство измерения углов).

3. Как по-другому можно записать данное равенство? Почему?

4. Данные равенства – математическая запись свойства смежных углов. Сформулируйте само свойство смежных углов.

∠СOD и ∠COF смежные, а
∠DOF – развернутый

∠DOF=∠COD+∠COF

∠СOD+∠COF= 180°

220 больше другого. Найдите величину каждого угла.


Решение:

Ответ: 790, 1010

∠AOB и ∠BOC смежные,
∠BOC - ∠AOB = 22°.

Дано:

Найти:

∠AOB , ∠BOC .

Пусть ∠AOB = x, тогда ∠BOC = x+22°.
По свойству смежных углов: ∠AOB + ∠BOC = 180°.
Значит, х +22+х =180,
2х = 180- 22,
2х = 158,
х = 158:2,
х = 79.
∠AOB = 79°, тогда ∠BOC = 79° +22°=101°.

B

A

C

O

одного угла являются дополнительными полупрямыми сторон другого.
∠AOB и ∠COD

вертикальные,
∠AOC и ∠BOD вертикальные

вертикальных углов AOC и BOD равны.
Доказательство:

из углов равен 460. Найти величины остальных углов.
Дано:

Найти:

Решение:

Ответ: 1340, 460, 1340

AD ∩ BC = О
∠AOB = 46°

∠AOC, ∠COD, ∠BOD.

ним: а) угол BOC
3. Запишите пары смежных углов,

имеющиеся на рисунке:

4. Запишите пары вертикальных углов, имеющиеся на рисунке:

качественной подготовки учителя на курсах повышения квалификации[текст]/Л.Ф. Батан// Толерантно-ориентированное

образование в поликультурном мире: материалы Международной научно-практической конференции, 1-2 ноября 2005 года, г. Новосибирск / Новосибирский институт повышения квалификации и переподготовки работников образования. – Новосибирск: Изд-во НИПКиПРО, 2005. – 244с. – 56-60
Батан, Л. Ф. Некоторые аспекты преподавания математики в свете новых информационных технологий [Текст]/ Л. Ф. Батан // Повышение качества современного образования: Методология. Теория. Практика. Межрегиональный сборник научных трудов. – Новосибирск: Издательство НИПКиПРО, 1998. – 28с.
Погорелов А. В. Геометрия: ччеб. Для 7-9 кл. общеобразоват. Учереждений / А.В. Погорелов. – 9-е изд. – М. : Просвещение, 2008. – 224с.
Сайт «Фестиваль педагогических идей «Открытый урок»» http://festival.1september.ru/articles/315086/

- смежные
Доказать: ∠AOC + ∠AOB = 180 °

Доказательство:

1. По свойству измерения углов ∠AOC + ∠AOB = ∠BOC

2. ∠BOC = 180° - развернутый

3. Т. е. ∠AOC + ∠AOB = 180°