- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Виды квадратных уравнений
Содержание
- 2. гипотезаКаждый человек, особенно если он ученик 8
- 3. вопросы...Определение квадратного уравненияВиды квадратных уравненийРешение квадратных уравнений
- 4. Квадратные уравнения - это фундамент, на котором
- 5. Уравнение вида
- 6. виды квадратных уравненийполныеквадратные уравнениянеполныеквадратные уравненияприведенное квадратное уравнение
- 7. Решение неполных квадратных уравнений
- 9. Способы решения квадратных уравнений Разложение левой части
- 10. Разложение левой части на множители
- 11. Метод выделения полного квадрата
- 12. Исполязование формул корней квадратного уравнения
- 13. примеры
- 14. Применение теоремы Виета
- 15. Введение новой переменнойУмножим обе части уравнения на
- 16. По сумме коэффициентов квадратного уравнения
- 17. Графический способ- Графиком функции является парабола- Графиком
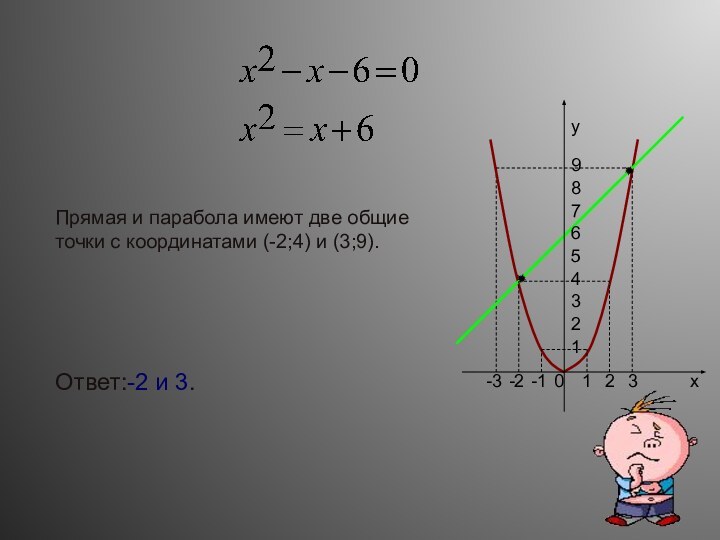
- 18. 0123-1-2-3123456789xyПрямая и парабола имеют две общие точки с координатами (-2;4) и (3;9).Ответ:-2 и 3.
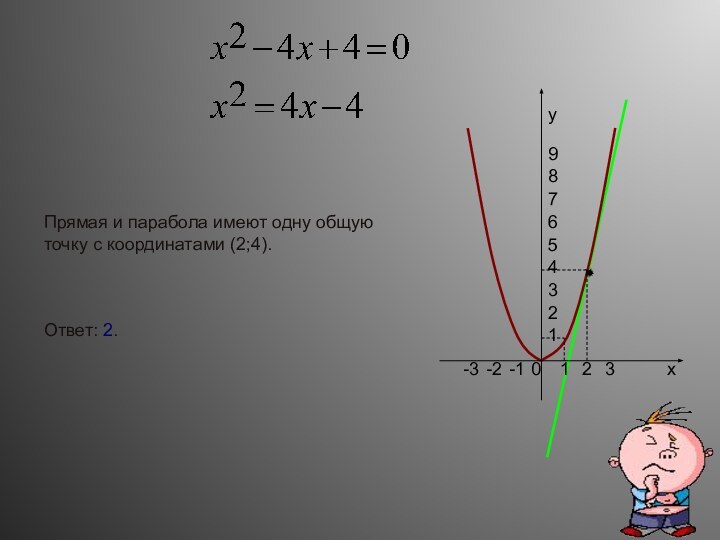
- 19. 0123-1-2-3123456789xyПрямая и парабола имеют одну общую точку с координатами (2;4).Ответ: 2.
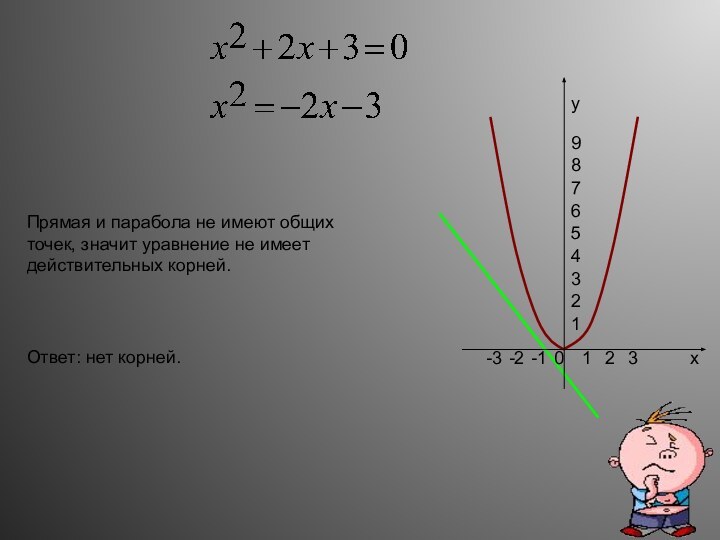
- 20. 0123-1-2-3123456789xyПрямая и парабола не имеют общих точек, значит уравнение не имеет действительных корней.Ответ: нет корней.
- 21. ВыводУ нас хорошие знания, поэтому мы можем
- 22. Скачать презентацию
- 23. Похожие презентации
гипотезаКаждый человек, особенно если он ученик 8 класса, может решить квадратное уравнение, если знает ответы на вопросы…



















Слайд 3
вопросы...
Определение квадратного уравнения
Виды квадратных уравнений
Решение квадратных уравнений
Слайд 4 Квадратные уравнения - это фундамент, на котором покоится
величественное здание алгебры. Квадратные уравнения находят широкое применение при
решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. В школьном курсе математики изучают формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Разберём некоторые из них.Слайд 5 Уравнение вида
, где
-переменная, - некоторые числа, , называется квадратным уравнением.Примеры:
Слайд 6
виды квадратных уравнений
полные
квадратные
уравнения
неполные
квадратные
уравнения
приведенное квадратное уравнение
Слайд 9
Способы решения
квадратных уравнений
Разложение левой части на
множители;
Метод выделения полного квадрата;
Применение формул корней квадратного
уравнения;Применение теоремы Виета;
Введение новой переменной;
По сумме коэффициентов квадратного уравнения;
Графический.
Слайд 15
Введение новой переменной
Умножим обе части уравнения на a
Пусть
тогда
Корни уравнения найдем по теореме, обратной теореме Виета
или
по сумме коэффициентов уравнения
Слайд 17
Графический способ
- Графиком функции является парабола
- Графиком функции
является прямая
Прямая и парабола имеют только одну общую
точку, значит уравнение имеет одно решение;Прямая и парабола имеют две общие точки, абсциссы этих точек являются корнями квадратного уравнения;
Прямая и парабола не имеют общих точек, значит уравнение не имеет корней.