- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к конкурсу Форум
Содержание
- 2. Автор:Пичковсная галина Михайловна
- 3. ЯЦКО ВЕРА-ученица 11 классаУчастники проекта:
- 4. Творческое название проектаИХ ВЕЛИЧЕСТВО –ЦИЛИНДРКОНУСШАР!
- 5. Какова роль темы: «Тела вращения» при изучении
- 6. «История возникновения тел вращения».«Понятие цилиндра, конуса, шара».-
- 7. Учебные темы: Цилиндр. Площадь поверхности цилиндра.
- 8. Цели и задачи проектаДидактические
- 10. Геометрическое тело – Часть пространства, отделённое от остальной части границей.
- 11. Цилиндр. Тело, ограниченное цилиндрической поверхностью
- 12. Немного истории.
- 13. В работах Евклида ничего не говорится о
- 14. Понятие цилиндра.Рассмотрим
- 15. Цилиндр называется прямым, если его образующие перпендикулярны
- 16. Цилиндрическая поверхность наз-ся боковой поверхностью цилиндра, а
- 17. Сечение цилиндра.Осевое Если секущая плоскость походит
- 18. Если плоскость сечения не параллельна основаниям цилиндра,
- 19. АДля того, чтобы легче понять как найти
- 20. За площадь боковой поверхности цилиндра принимается площадь
- 21. Объем цилиндра.Если
- 22. При выводе формулы для площади круга были
- 23. Построим две прямые призмы с основаниями Р
- 24. Несколько свойств цилиндра.Все образующие цилиндра параллельны и
- 26. 2.Радиус вписанной в правильный треугольник окружности
- 28. Задача: «Сечение цилиндра плоскостями».Осевое сечение цилиндра –
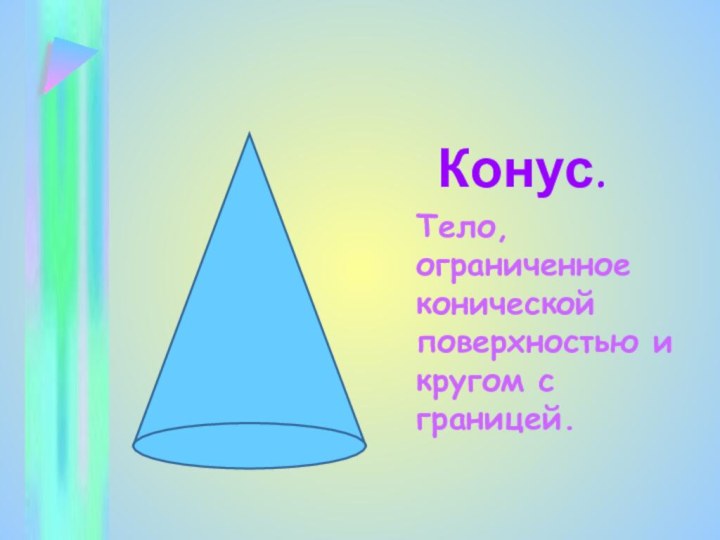
- 29. Конус. Тело, ограниченное конической поверхностью и кругом с границей.
- 30. АПрямой круговой конус (от греческого слова konos
- 32. С глубокой древности рассматриваются также конические поверхности,
- 33. Строгое доказательство
- 34. У Евклида нет понятия конической поверхности, оно
- 35. В сечении конуса плоскостью, параллельной его основанию,
- 36. Если плоскость сечения не параллельна основанию, то
- 37. Усеченный конус.В произвольном конусе проведем секущую плоскость,
- 38. Площадь боковой поверхности конусаЗа
- 39. Выразим а через L и r. Так
- 40. Объем
- 41. неограниченно приближаются к площади круга в основании
- 42. Дополним данный усеченный конус до полного. Пусть
- 43. Задача: «Сечение конуса»Конус пересечен плоскостью, параллельной основанию,
- 45. Сфера
- 46. Шар, так же как цилиндр и конус,
- 47. ОГраница шара называется шаровой поверхностью, или сферой.
- 48. В своих работах Евклид шару и его
- 49. Сечение шара плоскостью.Всякое сечение шара
- 50. Касательная плоскость к сфере.Плоскость, имеющая со сферой
- 53. Дано:Шар; m=10кг, р=7,2г/см3.Найти: Dш.Решение: Vш=m/p=10 000/7,2=1389 см3.Vш=4/3ПR3=ПD3/6.ПD3/6=1389, D3=2778, D=14см3.Ответ:D=14см3.
- 54. Нарисовать фигуру, полученную вращением треугольника относительно прямой,
- 55. Параболоидом вращения называется поверхность, которая получается при вращении параболы относительно оси Оу.У=ах2Оху
- 56. При вращении гиперболы относительно оси Оу получается поверхность, которая называется Гиперболоидом вращения
- 57. Она часто используется в архитектурных сооружениях. Например,
- 58. Учебный проект проводится на заключительном этапе изучения
- 59. «Считай несчастным тот час и тот день,
- 60. Скачать презентацию
- 61. Похожие презентации





















































Слайд 2
Автор:Пичковсная галина
Михайловна
Автор:
Пичковская Галина Михайловна
МОБУ Тумаковская средняя общеобразовательная
школа.
Слайд 5
Какова роль темы: «Тела вращения» при изучении геометрии?
Вопросы
учебной темы (проблемные):
Понятие непрямого цилиндра и конуса, вывод формул
площади поверхности цилиндра и конуса, объёма цилиндра и конуса разными способами.В каких областях применяются тела вращения и с какой целью?
Зачем решать задачи в геометрии на тела вращения?
Можно ли научиться строить тела вращения не школьной программы?
Кто подарил человечеству первые сведения о телах вращения?
Какова роль темы: «Тела вращения» при изучении геометрии?
Вопросы учебной темы (проблемные):
Понятие непрямого цилиндра и конуса, вывод формул площади поверхности цилиндра и конуса, объёма цилиндра и конуса разными способами.
В каких областях применяются тела вращения и с какой целью?
Зачем решать задачи в геометрии на тела вращения?
Можно ли научиться строить тела вращения не школьной программы?
Кто подарил человечеству первые сведения о телах вращения?
вопросы
Основополагающий вопрос
Слайд 6
«История возникновения тел вращения».
«Понятие цилиндра, конуса, шара».
-
«Объёмы цилиндра, конуса и шара».
- «Площади поверхностей цилиндра, конуса
и сферы».- «Сложные задачи, которые решаются с помощью формул: S=2πr(r+h), S= πrl,
S=4πR, V= πR2H, V=1/3πR2H, V=4/3πR3 Результаты представления исследований:
Презентация в Power-Point.
темы самостоятельных исследований:
Слайд 7
Учебные темы:
Цилиндр. Площадь поверхности цилиндра. Объём
цилиндра.
Конус. Площадь поверхности конуса. Объём конуса.
Сфера. Формула площади сферы.
Шар. Формула объёма шара.
Разные задачи на вписанные и описанные многогранники, цилиндр, конус и шар.
Учебные темы:
Слайд 8
Цели и задачи проекта
Дидактические цели
- Формирование математической грамотности и усвоения способов решения задач
на применение формул площадей и объёмов тел вращения.- Формирование критического мышления;
Формирование навыков исследовательской работы.
Формирование умения самостоятельно анализировать,синтезировать,делать выводы.
Развитие интереса к процессу познания на уроках математики.
Методические задачи
- Научить обрабатывать и обобщать полученную информацию в ходе исследований и сбора материала по данной теме.
Научить применять новые компьютерные технологии.
Научить различать полученные тела вращения.
-Научить кратко излагать свои мысли устно-письменно.
-Активизировать творческую деятельность учащихся.
Слайд 12
Немного истории.
«Геометрия приближает
разум к истине».
Платон.
В своих работах Евклид дает определение цилиндра, исходя из вращения прямоугольника около одной его стороны. Однако понятия цилиндрической поверхности у него нет; эти понятия встречаются у одного из его комментаторов - Серена из Антинои (Египет), жившего в IVв. Серен трактует и о наклонном цилиндре, в то время как Евклид имеет дело только с прямым круговым цилиндром. Общее понятие цилиндрической поверхности, получаемой движением образующей, пересекающей все точки некоторой направляющей, впервые вводит Б. Кавальери (XVII в.)
Слайд 13
В работах Евклида ничего не говорится о площади
боковой поверхности цилиндра, она была найдена Архимедом. В своих
произведениях он доказывает, что «поверхность всякого прямого цилиндра, за вычетом оснований, равна кругу, радиус которого есть средняя пропорциональная между стороной (образующей) цилиндра и диаметром его основания».
Слайд 14
Понятие цилиндра.
Рассмотрим 2
параллельные плоскости и окружность расположенную в одной из этих
плоскостей. Через каждую точку окружности проведем прямую, перпендикулярную к плоскости. Отрезки этих прямых, заключенныемежду плоскостями образуют цилиндрическую поверхность. А тело
ограниченное
цилиндрической
поверхностью и 2-мя
кругами с границами,
Называется ЦИЛИНДРОМ.
а
в
Слайд 15
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям
оснований. Прямой цилиндр можно получить при вращении прямоугольника вокруг
одной из его сторон.Слово«цилиндр» происходит от греческого kylindr
означает валик, каток.
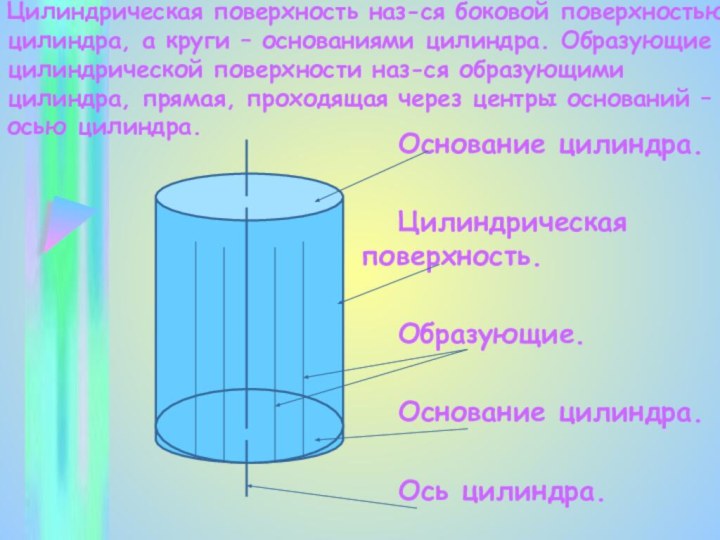
Слайд 16 Цилиндрическая поверхность наз-ся боковой поверхностью цилиндра, а круги
– основаниями цилиндра. Образующие цилиндрической поверхности наз-ся образующими цилиндра,
прямая, проходящая через центры оснований – осью цилиндра. Основание цилиндра.
Цилиндрическая поверхность.
Образующие.
Основание цилиндра.
Ось цилиндра.
Слайд 17
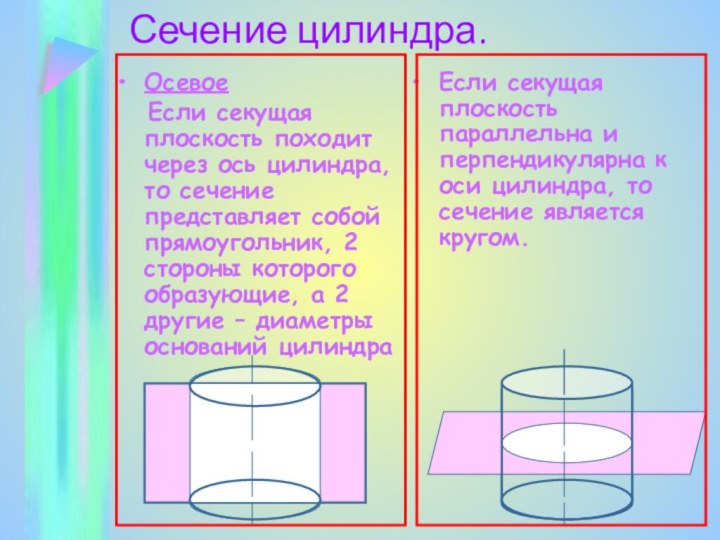
Сечение цилиндра.
Осевое
Если секущая плоскость походит через
ось цилиндра, то сечение представляет собой прямоугольник, 2 стороны
которого образующие, а 2 другие – диаметры оснований цилиндраЕсли секущая плоскость параллельна и перпендикулярна к оси цилиндра, то сечение является кругом.
Слайд 18
Если плоскость сечения не параллельна основаниям цилиндра, то
в сечении получится эллипс
Сечение цилиндра плоскостью, параллельной его оси,
дает прямоугольник, 2 стороны которого служат образующими цилиндра, а 2 другие – равные между собой хорды окружностей основания.
Слайд 19
А
Для того, чтобы легче понять как найти площадь
цилиндра, представим себе, что его боковую поверхность разрезали по
образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости а. В результате получился прямоугольник (развертка боковой поверхности цилиндра). Основание АС прямоугольника является разверткой окружности основания цилиндра, а высота АВ–образующей цилиндра,поэтому АС=2Пr, АВ=h, где r-радиус цилиндра, h-его высота.
h
2Пr
h
А
В
С
D
Слайд 20
За площадь боковой поверхности цилиндра принимается площадь ее
развертки.
Так как площадь прямоугольника АВДС=АС*АВ=2Пrh, то для вычисления площади
Sбок боковой поверхности цилиндра радиуса r и высоты h получается формула Sбок=2Пrh. Итак, площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна Пr2, то для вычисления площади Sцил полной поверхности цилиндра получаем формулу: Sцил=2Пr(r+h).
Слайд 21
Объем цилиндра.
Если тело
простое, т.е. допускает разбиение на конечное число треугольных пирамид,
то его объем равен сумме объемов этих пирамид. Для произвольного тела объем определяется следующим образом.Данное тело имеет объем V, если существуют содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколь угодно мало отличающихся от V.
Применим это определение к нахождению объема цилиндра с радиусом R и высотой Н.
Слайд 22
При выводе формулы для площади круга были построены
такие 2 n-угольника (один - содержащий круг, другой -содержащийся
в круге), что их площади при неограниченном увеличении n неограниченно приближались к площади круга. Построим такие многоугольники для круга в основании цилиндра. Пусть P-многоугольник, содержащий круг, а Р`-многоугольник, содержащийся в круге.
Слайд 23
Построим две прямые призмы с основаниями Р и
Р` и высотой Н, равной высоте цилиндра. Первая призма
содержит цилиндр, а вторая призма содержится в цилиндре. Т.к. при неограниченном увеличении n площади оснований призм неограниченно приближаются к площади основания цилиндра S, то их объемы неограниченно приближаются к SH. Согласно определению объем цилиндра V=SH=ПR2H.объем цилиндра равен произведению площади основания на высоту.
Слайд 24
Несколько свойств цилиндра.
Все образующие цилиндра параллельны и равны
друг другу.
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую
поверхность по окружности, равной окружности основания.Круговой цилиндр получается вращением прямоугольника вокруг любой его стороны.
Высота цилиндра равна его образующей.
Слайд 25
Задача.
1.В цилиндр вписана правильная треугольная призма, а
в последнюю вписан еще один цилиндр. Найти отношение объемов этих цилиндров.Решение:Оба цилиндра имеют равные высоты, поэтому их объемы относятся как площади длин оснований, т.е. как квадраты радиусов цилиндров.
V1=Пr2Н
V2=ПR2Н
Н=Н, V1=Пr2Н
V2=ПR2Н
r2/R2,
Слайд 26
2.Радиус вписанной в правильный треугольник окружности в
два раза меньше радиуса описанной окружности.
Найти отношение площадей.
Площадь вписанной в правильный треугольник окружности в четыре раза меньше площади описанной окружности.
r2/R2=12/22=1/4,т.к.
S=π r2
r
R
Слайд 27
Задача.
Дано: цилиндр, d=65cм(0,65м), Н=18м, 10% на
заклепку.Найти: Sбок+10%Sжести.
Решение: Sбок=2ПrН = 2*3,14*0,325*18=36,738(м2)
36,738-90%, 1%-36,738:90=0,408, 10%-40,8м2.
Ответ: На изготовление трубы необходимо 40,8м2 жести.
Слайд 28
Задача: «Сечение цилиндра плоскостями».
Осевое сечение цилиндра – квадрат,
площадь которого Q. Найти площадь основания цилиндра.
Решение. Сторона квадрата
√Q. Она равна диаметру основания. Поэтому площадь основания равна:П (√Q/2)2= П Q/4.
Слайд 30
А
Прямой круговой конус (от греческого слова konos –
«сосновая шишка») – это фигура, получающаяся при вращении прямоугольного
треугольника вокруг одного из его катетов.Треугольник АВС вращается около катета АС. Конус ограничен боковой поверхностью, образующийся при
вращении гипотенузы АВ,
и основанием – кругом,
получающимся при вра –
щении второго катета СВ.
А
В
С
Слайд 32
С глубокой древности рассматриваются также конические поверхности, составленные
из всех прямых пространства, пересекающих данную прямую (ось) в
одной точке (вершине), и образующие с осью данный, отличный от прямого, угол. Составляющие коническую поверхность называются образующими – они получаются из одной образующей вращением около оси, и поэтому такую коническую поверхность часто называют конусом вращения.
Слайд 33
Строгое доказательство теорем,
служащих для вывода формулы объема конуса дал Евдокс Книдский,
доказывая,Что объем конуса равен 1/3 объема цилиндра, имеющего то же основание и ту же высоту.
Что отношение объемов конусов (или цилиндров)с равными высотами равно отношению площадей их оснований.
Что объемы двух подобных конусов (или цилиндров), т.е таких, у которых оси и диаметры оснований пропорциональны, относятся как кубы диаметров.
Что отношение объемов двух конусов (или цилиндров), площади оснований которых равны, равно отношению высот.
Слайд 34
У Евклида нет понятия конической поверхности, оно было
введено Апполонием. Вот что он пишет: «Если от какой
– либо точки окружности круга, который не находится в одной плоскости с некоторой точкой, проводить прямые, соединяющие эту точку с окружностью, и при неподвижности точки перемещать прямую по окружности, возвращая ее туда, откуда началось движение, то поверхность описанную прямой и составленную из двух поверхностей, лежащих в вершине друг против друга, из которых каждая бесконечно увеличивается, если бесконечно продолжать описывающую прямую, я называю конической поверхностью, неподвижную же точку – ее вершиной, а осью-прямую, проведенную через эту точку и центр круга».
Слайд 35
В сечении конуса плоскостью, параллельной его основанию, получается
круг.
В сечении конуса плоскостью, проходящей через его ось (осевое
сечение), получается равнобедренный треугольник, боковыми сторонами которого служат образующие, а основанием – диаметр основания конуса.
Слайд 36
Если плоскость сечения не параллельна основанию, то в
сечении получается эллипс.
В сечении конуса плоскостью, проходящей через его
вершину и пересекающей его поверхность получается равнобедренный треугольник, боковыми сторонами которого служат образующие конуса, а основанием – хорда окружности его основания.
Слайд 37
Усеченный конус.
В произвольном конусе проведем секущую плоскость, перпендикулярную
к его оси. Эта плоскость пересекается с конусом по
кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называется основаниями усеченного конуса, а отрезок, соединяющий их центры,- высотой усеченного конуса.О1
О
Слайд 38
Площадь боковой поверхности конуса
За площадь
боковой поверхности конуса принимается площадь ее развертки. Выразим площадь
Sбок боковой поверхности конуса через его образующую L и радиус основания r. Площадь кругового сектора – развертки боковой поверхности конуса – равна , где α – градусная мера дуги АВА`, поэтому Sбок = П L2 α3600
L
В
А
А1
α
Слайд 39
Выразим а через L и r. Так как
длина дуги АВА` равна 2Пr (длине окружности основания конуса),
то 2Пr=П L а, откуда а=360 r. Подставив180 L
Это выражение в формулу, получим Sбок = Пr L.
Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Слайд 40
Объем конуса
Построим
два многоугольника в плоскости основания конуса: многоугольник Р, содержащий
основание конуса, и многоугольник P`, содержащийся в основании конуса. Первая пирамида содержит конус, а вторя пирамида содержится в конусе.Как мы знаем, существуют такие многоугольники Р и P`, площади которых при неограниченном увеличении числа их сторон n
Слайд 41
неограниченно приближаются к площади круга в основании конуса.
Для таких многоугольников объемы построенных пирамид неограниченно приближаются к
1/3SH, где S-площадь основания конуса, а Н-его высота. Согласно определению отсюда следует, что объем конуса V=1/3SH=1/3ПR2H.Объем конуса равен одной трети произведения площади основания на высоту.
Слайд 42
Дополним данный усеченный конус до полного. Пусть х-его
высота. Объем усеченного конуса равен разности объемов двух других
полных конусов: одного с радиусом основания R1 и высотой х, другого с радиусом основания R2 и высотой х-h.Так же объем любого усеченного конуса равен V=1/3H(S1+S2+√S1S2),
Где S1иS2 – площади оснований, а высота Н определяется как расстояние между плоскостями оснований.
Слайд 43
Задача: «Сечение конуса»
Конус пересечен плоскостью, параллельной основанию, на
расстоянии d от вершины. Найдите площадь сечения, если радиус
основания конуса R, а высота Н.Решение: Сечение конуса получается из основания конуса преобразованием гомотетии относительно вершины конуса с коэффициентом гомотетии k=d/H. Поэтому радиус круга в
сечении r=Rd/H. Следовательно, площадь сечения
S=П R2d2/H2 .
Слайд 44
Задача.
Дано: Палатка в виде конуса.
Конус,
d=4м, Н=3,5м, 5% на швы.Найти: Sбок+5%Sпарусины.
Решение: Sбок=ПrL, L=SA, треуг.ОSA - прямоуг. SA=√SO2+ОА2= √16,25
Sбок=3,14*2*√16,25=25м2.
25м-95%, х-100%,
Х=25*100/95=26,3м2.
Ответ: На изготовление пала-
тки необходимо 26,3м2
парусины.
О
S
А
Слайд 45 Сфера и
Шар.
Точки пространства, удаленные от данной точки О на данное
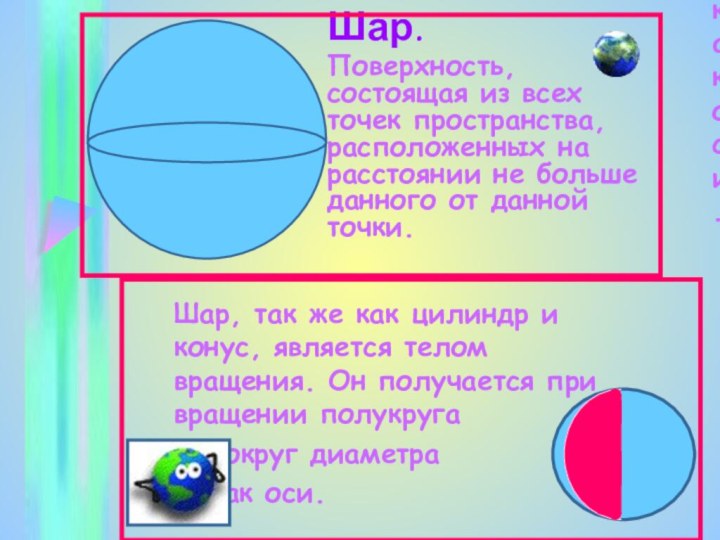
расстояние R, образуют сферу с центром О и радиусом R. Сфера ограничивает шар, состоящий из точек, удаленных от О на расстояние, не больше R. Эти геометрические объекты так же как окружность и круг, рассматривали еще в глубокой древности. Открытие шарообразности Земли, появление представлений о небесной сфере дала толчок к развитию специальной науки – сферики, изучающей расположение на сфере фигуры.Слайд 46 Шар, так же как цилиндр и конус, является
телом вращения. Он получается при вращении полукруга
вокруг диаметра
как оси.
Шар.
Поверхность, состоящая из всех точек пространства, расположенных на расстоянии не больше данного от данной точки.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга
вокруг диаметра
как оси.
Слайд 47
О
Граница шара называется шаровой поверхностью, или сферой. Таким
образом, точками сферы являются все точки шара, которые удалены
от центра на расстоянии, равном радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом. ОК – радиус шара.Отрезок, соединяющий две
точки шаровой поверхности
и проходящей через центр
шара называется диаметром.
О
К
R
М
Слайд 48
В своих работах Евклид шару и его поверхности
уделяет сравнительно мало внимания. Он доказывает, что объемы двух
шаров относятся как кубы их радиусов. Ни площади поверхности шара, ни объема Евклид не вычисляет, вероятно он их и не знал. Архимед первый открыл соответствующие формулы. Так же Архимед доказал следующие утверждения:«Каждый шар в четыре раза больше конуса, основание которого равно большому кругу шара, а высота – радиусу последнего».
«Цилиндр, основание которого равно большому кругу шара, а высота – диаметру последнего, в полтора раза больше шара».
Слайд 49
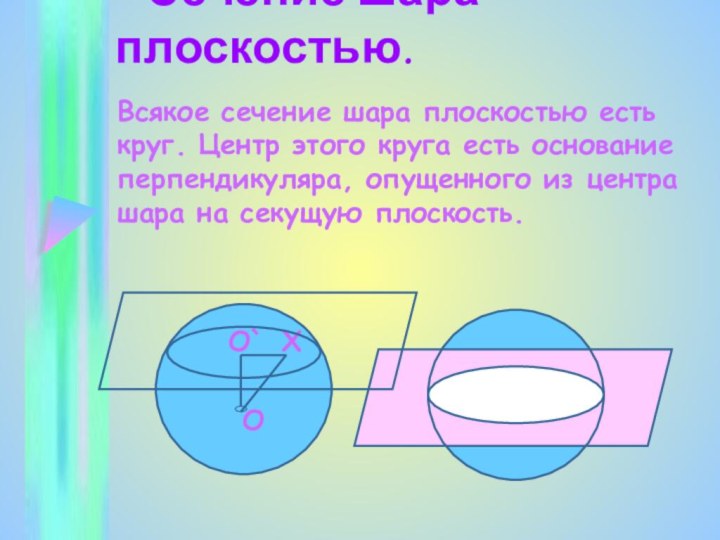
Сечение шара плоскостью.
Всякое сечение шара плоскостью
есть круг. Центр этого круга есть основание перпендикуляра, опущенного
из центра шара на секущую плоскость.О`
О
Х
Слайд 50
Касательная плоскость к сфере.
Плоскость, имеющая со сферой только
одну общую точку, называют касательной плоскостью к сфере, а
их общая точка называется точкой касания плоскости и сферы.Теорема: Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец,
лежащей на сфере, то эта
плоскость является
касательной к сфере.
А
О
Слайд 51
Площадь
сферы.
Видно, что площадь поверхности описанного многогранника при неограниченном уменьшении
размеров его граней, стремятся к 4ПR2. Поэтому величина 4ПR2 принимается за площадь сферы.Итак, площадь сферы радиуса R вычисляется по формуле S=4ПR2.
Аналогично определяется площадь сферической части поверхности шарового сектора, т.е. площадь сферического сегмента, для нее получается формула: S=2ПRH, где Н – высота сегмента.
Слайд 52
Объем шара.
Введем
декартовы координаты, приняв центр шара за начало координат. Плоскость ху пересекает поверхность шара радиуса R по окружности, которая, как известно, задается уравнением х2+у2=R2.Полуокружность, расположенная над осью х, задается уравнением у=f(х)=+√R2-х2, -R<х≤R.
Поэтому объем шара определяется по формуле:
R R
V= П ∫ (R2-х2)dx=П (R2x- х3/3) =4/3П R3.
-R -R
-R
y
x
О
Слайд 53
Дано:
Шар; m=10кг, р=7,2г/см3.
Найти: Dш.
Решение: Vш=m/p=10 000/7,2=
1389 см3.
Vш=4/3ПR3=ПD3/6.
ПD3/6=1389, D3=2778,
D=14см3.
Ответ:D=14см3.
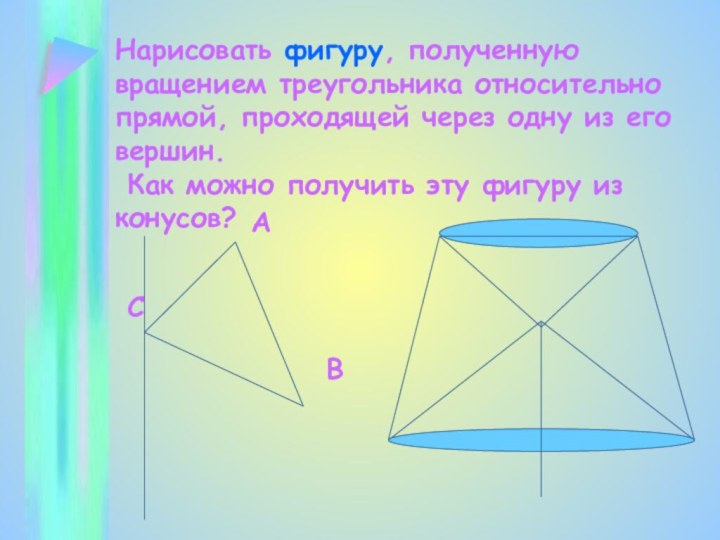
Слайд 54 Нарисовать фигуру, полученную вращением треугольника относительно прямой, проходящей
через одну из его вершин. Как можно получить эту
фигуру из конусов?А
В
С
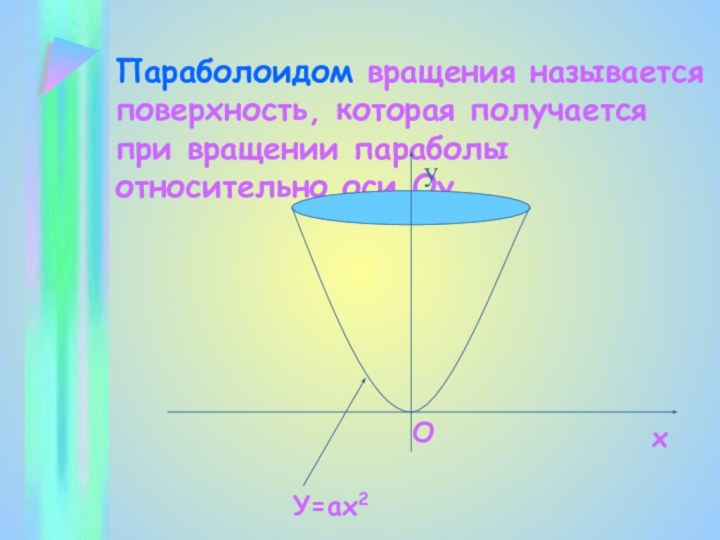
Слайд 55 Параболоидом вращения называется поверхность, которая получается при вращении
параболы относительно оси Оу.
У=ах2
О
х
у
Слайд 56 При вращении гиперболы относительно оси Оу получается поверхность,
которая называется Гиперболоидом вращения
Слайд 57 Она часто используется в архитектурных сооружениях. Например, Шуховская
башня в Москве на Шаболовке составлена из частей гиперболоида
вращения.
Слайд 58 Учебный проект проводится на заключительном этапе изучения темы
11 класса «ТЕЛА ВРАЩЕНИЯ», как повторительно-обобщающий.
Проект имитирует научную, производственную
деятельность. На этом уроке моделируются самые разнообразные жизненные и производственные ситуации, целью которых становится изучение собранного материала, закрепление изученного и расширение кругозора. Учеников ставят в условия, когда нужно решать производственные задачи, что даёт им почувствовать себя взрослыми, принимающими серьёзные деловые решения. Этот проект позволяют развивать мышление школьников, умение приобретать знания из различных источников, анализировать факты, делать обобщение, высказывать собственные суждения, критически относиться к мнениям других. Приведены примеры решений задач на нахождения площадей и объёмов тел вращения, необходимые для ЕГЭ.Аннотация
Аннотация
Слайд 59
«Считай несчастным тот час и тот день, в
который ты не усвоил ничего нового и ничего не
прибавил к своему образованию».Ян Амос Коменский.



![Методические рекомендации для родителей для автоматизации звуков [р] и [рь] у детей на материале лексической темы Одежда. учебно-методический материал (средняя, старшая, подготовительная группа)](/img/tmb/8/744201/4ecd0bf12805a858d0402b34566ecf1f-210x.jpg)