- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Многогранники
Содержание
- 2. Примеры многогранников
- 3. Додекаэдр — двенадцатигранник, составленный из двенадцати правильных. Каждая вершина додекаэдра является
- 4. Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно)
- 5. Пирамида — многогранник, основание которого — многоугольник , а остальные грани — треугольники,
- 6. Конус — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из
- 7. невыпуклый многогранник-это такой многогранник, который при проведении
- 8. Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани
- 9. ПризмаПризма многогранник, у которого две грани — n -угольники
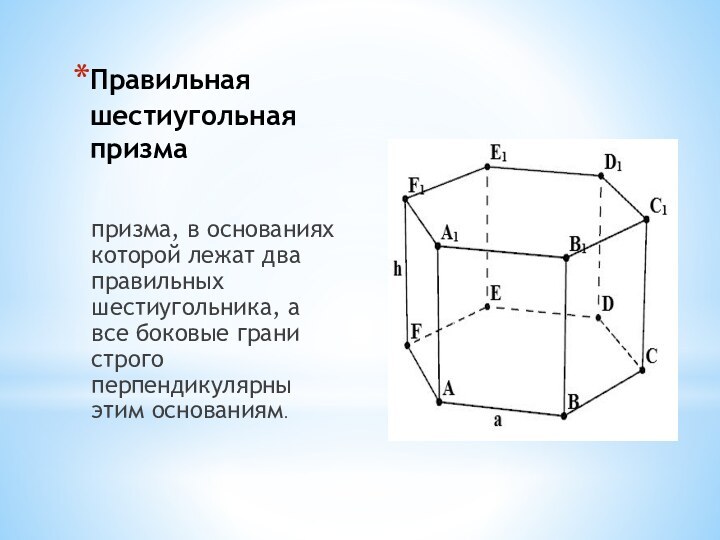
- 10. Виды призмы N-угольная призма Прямая пятиугольная призма Наклонная четырехугольная призмаПравильная шестиугольная призма
- 12. Прямая пятиугольная призма Если все боковые
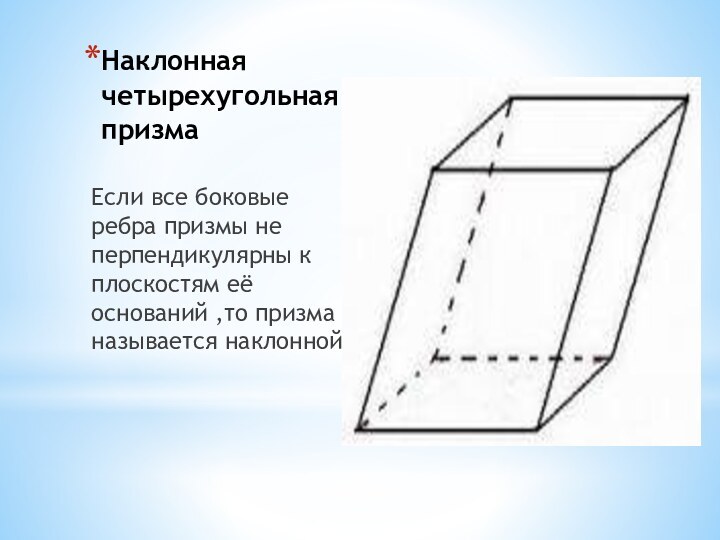
- 13. Наклонная четырехугольная призма Если все боковые ребра
- 14. Скачать презентацию
- 15. Похожие презентации
Примеры многогранников











Слайд 3 Додекаэдр — двенадцатигранник, составленный из двенадцати правильных. Каждая вершина додекаэдра является вершиной
трёх правильных пятиугольников.
Таким образом, додекаэдр имеет 12 граней (пятиугольных),
30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Сумма плоских углов при каждой из 20 вершин равна 324°.Додекаэдр имеет три звёздчатые формы.
Слайд 4 Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник,
у которого шесть граней и каждая из них —
параллелограмм. Различается несколько типов параллелепипедов:Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники;
Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники;
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикуляры
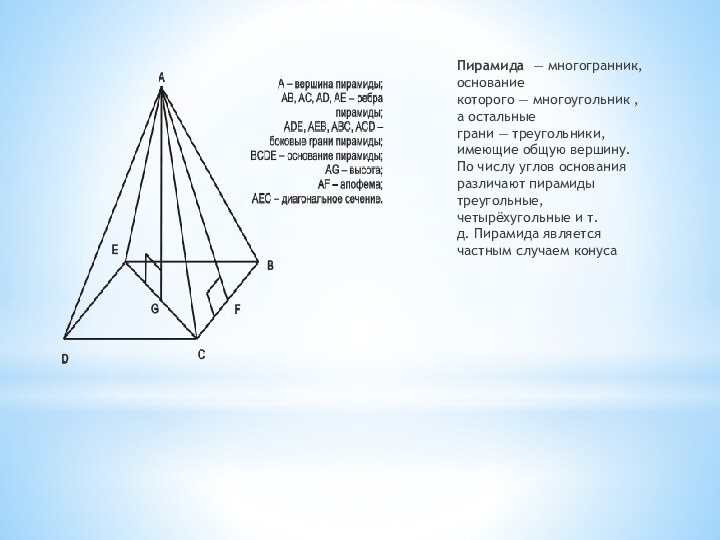
Слайд 5 Пирамида — многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие
общую вершину. По числу углов основания различают пирамиды треугольные,
четырёхугольные и т. д. Пирамида является частным случаем конусаСлайд 6 Конус — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной
точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом
называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Слайд 7
невыпуклый многогранник-это
такой многогранник, который при проведении плоскости
через любую его грань, целиком лежит по одну сторону
от этой плоскости. Либо надо дать определение так: Невыпуклым многогранником называется такой многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.ПРИМЕР:
Слайд 8 Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого
пересекаются между собой. Как и у не звёздчатых многогранников, грани
попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами.Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.
Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует всего 4 правильных звёздчатых тела, не являющиеся соединениями Платоновых и звёздчатых тел, называемые телами Кеплера — Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра. Остальные правильные звёздчатые многогранники являются или соединениями Платоновых тел, или соединениями тел Кепплера — Пуансо.