- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Формулы сокращенного умножения (7 класс)
Содержание
- 2. "Математику нельзя изучить, наблюдая, как это делает другой!"А. Нивен
- 3. *Исторические сведения:
- 4. *Бином Ньютона
- 5. Знаменита цитата из «Мастера и Маргариты» М.
- 6. Бином (лaт. bis − два, nomen -
- 7. Исаак Ньютон 1643-1727Сэр Исаа́к Нью́тон —
- 8. Бином Ньютона – формула, выражающая целую положительную
- 9. *Треугольник Паскаля
- 10. Столь необычные свойства позволяют считать треугольник Паскаля
- 11. Слева изображено несколько строк числового треугольника,
- 12. Блез Паска́ль — французский — французский математик
- 13. n = 0;
- 14. Степени биномов:
- 15. Тест
- 16. Продолжите формулу:
- 17. Продолжите формулу:
- 18. Продолжите формулу:
- 19. Продолжите формулу:
- 20. Продолжите формулу: правильного ответа нет
- 21. Продолжите формулу:
- 22. Продолжите формулу:
- 23. Продолжите формулу: правильного ответа нет
- 24. Продолжите формулу:
- 25. Разложите на множители: правильного ответа нет
- 26. Проверка
- 27. Продолжите формулу:Квадрат суммы
- 28. Продолжите формулу:Куб разности
- 29. Продолжите формулу:Произведение разности двух выражений и их суммы
- 30. Продолжите формулу:Разность кубов
- 31. Продолжите формулу: правильного ответа нетРазность квадратов
- 32. Продолжите формулу:Куб суммы
- 33. Продолжите формулу:Квадрат разности
- 34. Продолжите формулу: правильного ответа нетСумма квадратов, формулы нет
- 35. Продолжите формулу:Сумма кубов
- 36. Разложите на множители: правильного ответа нетРазность квадратов
- 37. Применение формул сокращенного умножения
- 38. (2 - 1)(2 +1)(22 +1 )(24 +1 )(28 +1 )(216 +1) – 232 =Вычислить:
- 39. Решение:(2 - 1)(2 +1)(22 +1 )(24 +1
- 40. Вычислить:992
- 41. Решение:992 =(100 -1)2 =1002 - 2∙100∙1 + 12=10000 - 200 + 1 =9801
- 42. Блез Паскаль (1623-1662) выдающийся математик, физик, философ
- 43. Математический фокус
- 44. «Отгадывание задуманного числа» Задумайте число (до 10);Умножьте
- 46. Возведение в квадрат…25² = 2 ∙ 3
- 47. Работа в парах:ИГРА «МАТЕМАТИЧЕСКАЯ МОЗАИКА».
- 48. Работа в парах:За 1 минуту из предложенных
- 49. Проверяем:(3х + 5у)2 = 9х2 + 30ху
- 50. Работа в парах:Тест-соответствие:
- 51. Работа в парах:Расшифровка:ДИОФАНТ
- 52. *Исторические сведения:«Диофант»
- 53. Диофант и его труды. О подробностях жизни Диофанта
- 54. Зато место жительства Диофанта хорошо известно –
- 55. В начале своего труда Диофант поместил краткое
- 56. В Палатинской антологии содержится эпиграмма–задача Метродора о
- 57. Домашнее задание:
- 58. Рефлексия:“Я понял(а)…“Я запомнил(а)…“Мне на уроке…“Я думаю…“Мне понравилось…
- 59. Подведение итогов урока:Подсчёт баллов и выставление оценок за урок
- 60. Спасибо за внимание!
- 61. Применение формул сокращенного умножения
- 62. Вычислить:272 – 372 =
- 63. Решение:272 – 372 =(27 – 37)(27+ 37) =– 10 ∙ 64 = – 640
- 64. Вычислить:32 ∙ 28 =
- 65. Решение:32 ∙ 28 =(30 + 2)(30 –
- 66. Вычислить:482 – 2∙48∙68 + 682 =
- 67. Скачать презентацию
- 68. Похожие презентации































































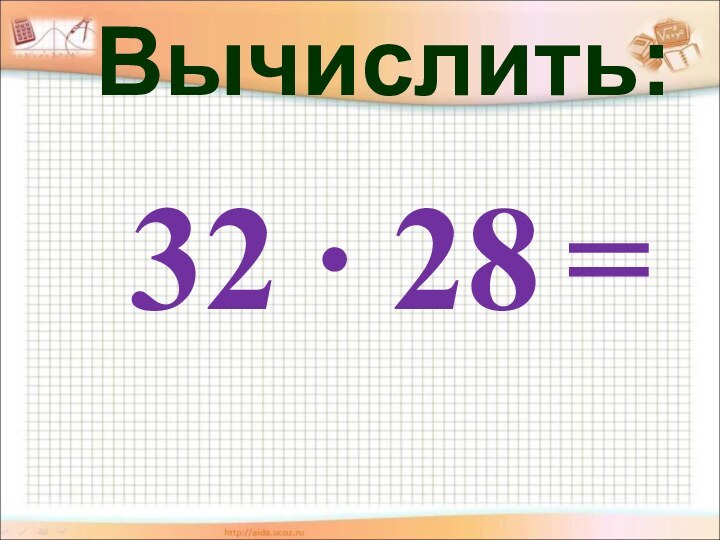



Слайд 5
Знаменита цитата из «Мастера и Маргариты»
М. А.
Булгакова: «Подумаешь, бином Ньютона!».
Бином Ньютона
в художественной
литературе. Бином Ньютона в художественной литературе появляется в нескольких запоминающихся контекстах, где речь идет о чем-либо сложном.
В рассказе А. Конан Дойля «Последнее дело Холмса»
Холмс говорит о математике профессоре Мориарти:
«Когда ему исполнился двадцать один год, он
написал трактат о биноме Ньютона, завоевавший ему
европейскую известность. После этого он получил кафедру
математики в одном из наших провинциальных
университетов, и, по всей вероятности, его ожидала
блестящая будущность».
Слайд 6 Бином (лaт. bis − два, nomen - имя)
или двучлен — частный случай
многочлена (полинома), который
состоит
из двух слагаемых одночленов (мономов).
Например:
a + b, a − b, a2 + b2, 3b −4b3
Слайд 7
Исаак Ньютон
1643-1727
Сэр Исаа́к Нью́тон — английский
— английский физик — английский физик, математик — английский
физик, математик, механик — английский физик, математик, механик и астроном — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета — английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.В 1664-1665 гг И. Ньютон установил, что формула, выражающая степень двучлена в виде суммы одночленов, обобщается на случай произвольных (дробных и отрицательных) показателей
Слайд 8
Бином Ньютона – формула, выражающая целую
положительную степень
суммы двух слагаемых
(двучлена, бинома) через степени этих слагаемых.
Частными
случаями бинома Ньютона являютсяформулы квадрата и куба суммы
двух слагаемых a и b
Бином Ньютона
Слайд 10 Столь необычные свойства позволяют считать треугольник Паскаля одной
из наиболее изящных схем во всей математике. Мартин Гарднер
Треугольник
Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего.
Слайд 11
Слева изображено несколько строк числового треугольника, образованного
по следующему правилу: по краям каждой строки стоят единицы,
а каждое из остальных чисел равно сумме двух стоящих над ним чисел предыдущей строки.В такой форме треугольник приведен в
«Трактате об арифметическом треугольнике» французского математика
Б. Паскаля (1623-1662), опубликованном
в 1665 году уже после смерти автора.
Блез Паскаль и его треугольник.
Несколько иные варианты этой числовой таблицы встречались столетием раньше у итальянского математика Н. Тартальи, а за несколько веков до этого у восточного ученого и поэта Омара Хайяма, некоторых китайских и индийских ученых.
Слайд 12 Блез Паска́ль — французский — французский математик —
французский математик, механик — французский математик, механик, физик —
французский математик, механик, физик, литератор — французский математик, механик, физик, литератор и философ — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.Блез Паскаль (1623-1662)
Слайд 13 n = 0;
1
n = 1; 1 1
n = 2; 1 2 1
n = 3; 1 3 3 1
n = 4; 1 4 6 4 1
n = 5; 1 5 10 10 5 1
n = 6; 1 6 15 20 15 6 1
n = 7; 1 7 21 35 35 21 7 1
Треугольник Паскаля
Слайд 39
Решение:
(2 - 1)(2 +1)(22 +1 )(24 +1 )(28
+1 )(216 +1) – 232 =
(22 - 1)(22 +1
)(24 +1 )(28 +1 )(216 +1) – 232 =(24 - 1)(24 +1 )(28 +1 )(216 +1) – 232 =
(28 - 1)(28 +1 )(216 +1) – 232 =
(216 - 1)(216 +1) – 232 =
(232 - 1) – 232 =
= – 1
Слайд 42
Блез Паскаль
(1623-1662)
выдающийся математик,
физик,
философ и писатель.
«Предмет математики настолько серьезен, что
полезно не упускать случая сделать его немного занимательным»
Слайд 44
«Отгадывание задуманного числа»
Задумайте число (до 10);
Умножьте его
на себя;
Прибавьте к результату задуманное число;
К полученной сумме прибавьте
1;К полученному числу прибавьте задуманное число.
Слайд 45
Решение:
x² + x + 1 + x
= x² + 2x + 1 = (x + 1)²
Например:
5·5 + 5 + 1 + 5 = 36,
тогда x = √36 – 1 = 6 – 1 = 5.
Слайд 46
Возведение в квадрат…
25² = 2 ∙ 3 +
25 = 625;
65² = 6 ∙ 7 + 25
= 4225;95² = 9 ∙ 10 + 25 = 9025;
105² = 10 ∙ 11 + 25 = 11025.
15² = 1 ∙ 2 + 25 = 225;
55² = 5 ∙ 6 + 25 = 3025;
Слайд 48
Работа в парах:
За 1 минуту из предложенных выражений
составить формулы. Кто больше. 3х , 5у, 9х2, 30ху, 27х3,
125у3, 15ху, 25у2.
Слайд 49
Проверяем:
(3х + 5у)2 = 9х2 + 30ху +
25у2
(3х – 5у)2 = 9х2 – 30ху + 25у2
(5у
+3х)2 = 25у2 + 30ху + 9х2(5у – 3х)2 = 25у2 – 30ху + 9х2
(3х – 5у)(3х + 5у) = 9х2 – 25у2
(5у – 3х)(5у + 3х) = 25у2 – 9х2
(3х + 5у)(9х2 – 15ху + 25у2 ) = 27х3 +125у3
(3х – 5у)(9х2 + 15ху + 25у2 ) = 27х3 – 125у3
(5у + 3х)(25у2 – 15ху + 9х2) = 125у3 + 27х3
(5у – 3х)(25у2 + 15ху + 9х2) = 125у3 – 27х3
Слайд 53
Диофант
и его труды.
О подробностях жизни Диофанта Александрийского практически
ничего не известно..
Диофант представляет одну из наиболее трудных
загадок в истории науки. Нам не известно ни время, когда он жил, ни предшественники, которые работали бы в той же области. Труды его подобны сверкающему огню среди непроницаемой тьмы.Слайд 54 Зато место жительства Диофанта хорошо известно – Александрия,
центр научной мысли эллинистического мира. Наиболее загадочным представляется
творчество Диофанта. До наших дней дошли два произведения Диофанта, оба не полностью. Это «Арифметика» (шесть книг из тринадцати) и отрывки из трактата «О многоугольных числах». С именем этого учёного связано появление и развитие алгебраической геометрии, проблемами которой впоследствии занимались Леонард Эйлер, Карл Якоби и другие авторы. Известны и другие сочинения Диофанта.Труды Диофанта имели фундаментальное значение для развития алгебры и теории чисел.
Слайд 55 В начале своего труда Диофант поместил краткое введение,
ставшее первым изложением основ алгебры. В то время, все
алгебраические утверждения выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел - с объемом и т.д. Диофант стал первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям. В этой книге он построил поле рациональных чисел и ввёл буквенную символику. Там же сформулировал правила действий с многочленами и уравнениями. Так появились формулы, которые стали называться формулами сокращенного умножения.Слайд 56 В Палатинской антологии содержится эпиграмма–задача Метродора о Диофанте,
из которой можно сделать вывод, что Диофант прожил 84
года:Здесь погребен Диофант, и камень могильный
При счете расскажет нам,
Сколь долог был его век.
Велением бога он мальчиком был шестую часть своей жизни;
В двенадцатой части затем прошла его светлая юность.
Седьмую часть жизни прибавим – перед нами очаг Гименея.
Пять лет протекли; и прислал Гименей ему сына.
Но горе ребенку! Едва половину он прожил
Тех лет, что отец, как скончался несчастный.
Четыре года страдал Диофант от утраты такой тяжелой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть воспринял Диофант?
Диофант – последний из великих математиков античности.





























