Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

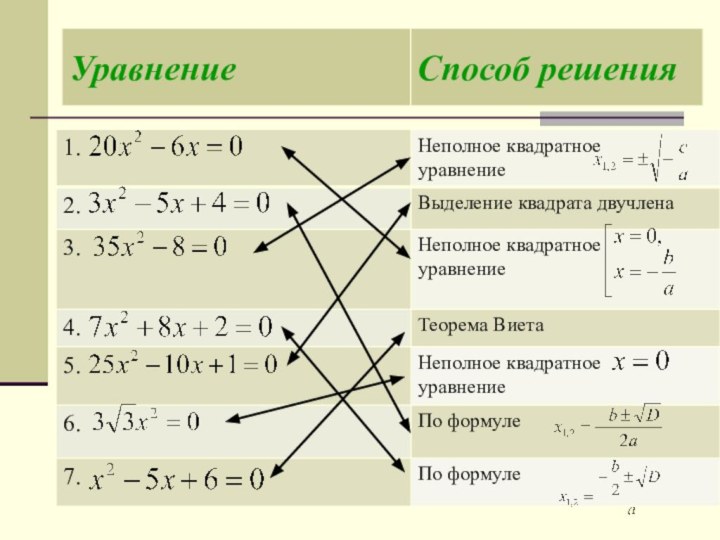
Презентация на тему Урок с презентацией Квадратные уравнения

Содержание

Квадратные уравнения
Квадратные уравнения(методы решения) Квадратные уравнения Методы решения уравнения I. Азбука квадратного уравнения Неполные квадратные уравнения I. Азбука квадратного уравненияПо формуле корней I. Азбука квадратного уравнения6. Теорема Виета II. Специальные методыЦель: Привести уравнение общего вида к неполному квадратному уравнению. Пригласительный билетI вариант Пригласительный билетI I вариант Пригласительный билетI вариант Гипотеза 1 Если в квадратном уравнении a+b+c=0, то один из корней равен 1, Пригласительный билетI I вариант Гипотеза 2 Если в квадратном уравнении a-b+c=0, то один из корней равен -1, II. Специальные методы 8. Если в квадратном уравнении a+b+c=0, то один из корней Самостоятельная работаI вариантII вариант ДиофантИз «Арифметики Диофанта» Михаэль Штифель (1487 – 1567)Из «Арифметики» Штифеля Спасибо за внимание!
Слайды презентации

Слайд 2 Квадратные уравнения

Квадратные уравнения

Слайд 3 Методы решения уравнения

Методы решения уравнения

Слайд 4 I. Азбука квадратного уравнения
Неполные квадратные уравнения

I. Азбука квадратного уравнения Неполные квадратные уравнения

Слайд 5 I. Азбука квадратного уравнения
По формуле корней

I. Азбука квадратного уравненияПо формуле корней

Слайд 6 I. Азбука квадратного уравнения
6. Теорема Виета

I. Азбука квадратного уравнения6. Теорема Виета

Слайд 7 II. Специальные методы
Цель: Привести уравнение общего вида к

II. Специальные методыЦель: Привести уравнение общего вида к неполному квадратному уравнению.

неполному квадратному уравнению.



Ответ: 2, 4.
Замечание: метод

применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения.

7. Метод выделения квадрата двучлена

Слайд 8

Слайд 9 Пригласительный билет
I вариант

Пригласительный билетI вариант

Слайд 10 Пригласительный билет
I I вариант

Пригласительный билетI I вариант

Слайд 11 Пригласительный билет
I вариант

Пригласительный билетI вариант

Слайд 12 Гипотеза 1
Если в квадратном уравнении a+b+c=0, то один

Гипотеза 1 Если в квадратном уравнении a+b+c=0, то один из корней равен

из корней равен 1, а второй по теореме Виета

равен

Слайд 13 Пригласительный билет
I I вариант

Пригласительный билетI I вариант

Слайд 14 Гипотеза 2
Если в квадратном уравнении a-b+c=0, то один

Гипотеза 2 Если в квадратном уравнении a-b+c=0, то один из корней равен

из корней равен -1, а второй по теореме Виета

равен

Слайд 15 II. Специальные методы
8. Если в квадратном уравнении a+b+c=0,

II. Специальные методы 8. Если в квадратном уравнении a+b+c=0, то один из

то один из корней равен 1, а второй по

теореме Виета равен

9. Если в квадратном уравнении
a-b+c=0, то один из корней равен -1, а второй по теореме Виета равен


На основании теорем

Слайд 16 Самостоятельная работа
I вариант

II вариант

Самостоятельная работаI вариантII вариант

Слайд 17 Диофант
Из «Арифметики Диофанта»

ДиофантИз «Арифметики Диофанта»

Слайд 18 Михаэль Штифель (1487 – 1567)
Из «Арифметики» Штифеля

Михаэль Штифель (1487 – 1567)Из «Арифметики» Штифеля
  • Имя файла: urok-s-prezentatsiey-kvadratnye-uravneniya.pptx
  • Количество просмотров: 171
  • Количество скачиваний: 1
- Предыдущая Презентация к уроку физики на тему: Влажность воздуха
Следующая - Презентация Путешествие по Азовскому морю

Похожие презентации

Урок Логарифмы Урок Логарифмы 139
Векторы Векторы 144
Сложение и вычитание одночленов Сложение и вычитание одночленов 182
Презентация по математике на тему Комплексные числа Презентация по математике на тему Комплексные числа 158
Мастер – класс по математике Мастер – класс по математике 78
Решу ВПР: простейшие текстовые задачи. Часть 5 Решу ВПР: простейшие текстовые задачи. Часть 5 181
Презентация по алгебре на тему Квадратичная функция (9 класс) Презентация по алгебре на тему Квадратичная функция (9 класс) 203
Презентация к уроку Свойства арифметического квадратного корня (8 класс) Презентация к уроку Свойства арифметического квадратного корня (8 класс) 295
Презентация к научно-исследовательской работе Метод координат Презентация к научно-исследовательской работе Метод координат 169
Презентация по темеСвойства логарифмов Презентация по темеСвойства логарифмов 170
Презентация по алгебре на тему: Линейные уравнения с двумя переменными (7 класс) Презентация по алгебре на тему: Линейные уравнения с двумя переменными (7 класс) 195
Презентація на тему Квадратні рівняння (8 клас) Презентація на тему Квадратні рівняння (8 клас) 525
Презентация по теме Показательная функция. График, свойства. Презентация по теме Показательная функция. График, свойства. 152
Практическое занятие элективного курса Функция: просто, сложно, интересно по теме Монотонность функции (9 класс) Практическое занятие элективного курса Функция: просто, сложно, интересно по теме Монотонность функции (9 класс) 175
Презентация по математике + экономика по теме: Легко ли прожить на пенсию Презентация по математике + экономика по теме: Легко ли прожить на пенсию 177
Обобщающий урок по теме Рациональные неравенства Обобщающий урок по теме Рациональные неравенства 208
Логарифм числа Логарифм числа 160
Решу ВПР: анализ диаграмм. Часть 5 Решу ВПР: анализ диаграмм. Часть 5 222
Элементы математической статистики Элементы математической статистики 117
Неравенства с одной переменной Неравенства с одной переменной 151
Урок одной задачи. Решение тригонометрических уравнений разными способами Урок одной задачи. Решение тригонометрических уравнений разными способами 118
Формулы Формулы 169
Презентация и разработка математической игры Конкурс умных и находчивых Презентация и разработка математической игры Конкурс умных и находчивых 188
Презентация по математике на тему Тригонометрические функции и их свойства (10 класс) Презентация по математике на тему Тригонометрические функции и их свойства (10 класс) 200
Квадратные уравнения Квадратные уравнения 149
Квадратичная функция алгебра Квадратичная функция алгебра 171
Производные функций Производные функций 148
Презентация к внеклассному мероприятию А.Н.Колмогоров-один из основоположников теории вероятностей Презентация к внеклассному мероприятию А.Н.Колмогоров-один из основоположников теории вероятностей 198
Графики степенных функций Графики степенных функций 194
Интеллектуальная игра Что? Где? Когда? Интеллектуальная игра Что? Где? Когда? 156