Презентация на тему теорема Виета

вида, неполных квадратных уравнений.
Рассмотреть и доказать теорему Виета и

b, c –
действительные числа,
причём а ≠ 0.

ax2

неполными, если хотя бы один из коэффициентов b или

с имеют разные знаки
Нет корней, если:
а и с имеют

2 корня:

Решения неполных квадратных уравнений.

- корней нет

- один корень

- два корня

Решение полного квадратного уравнения.

= 0
3) х² + 4x = 0
4) 4х² -

x1 = 1; x2 = .

x1 = 6; x2 = - 6.

x1 = 0; x2 = - 4.

Нет корней.

x = 0.

x = - 5

приведённым (а=1).
Квадратное уравнение общего вида можно привести к приведённому:

где

являются корнями уравнения
х2+рх+q=0
то справедливы формулы

т.е.сумма корней

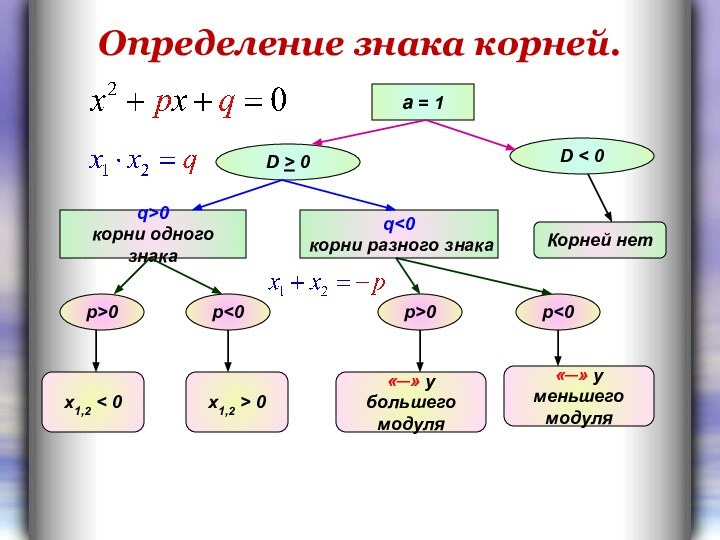
Теорема Виета.

Доказательство теоремы Виета.

Получаем корни:

или

Сложив оба корня, получаем:

Перемножив эти равенства, по формуле разности квадратов получаем:

Доказательство рассмотреть самостоятельно.

х2+рх+q=0

Теорема Виета и обратная ей:

(1,3,5)


По теореме, обратной теореме Виета:

0
Корней нет
q>0
корни одного знака
q0
p

x1,2 > 0

x1,2 < 0

p>0

p<0

«─» у большего
модуля

«─» у меньшего
модуля

- 5
5
6
- 6
- 7

7

6

- 6

- 6

1

- 1

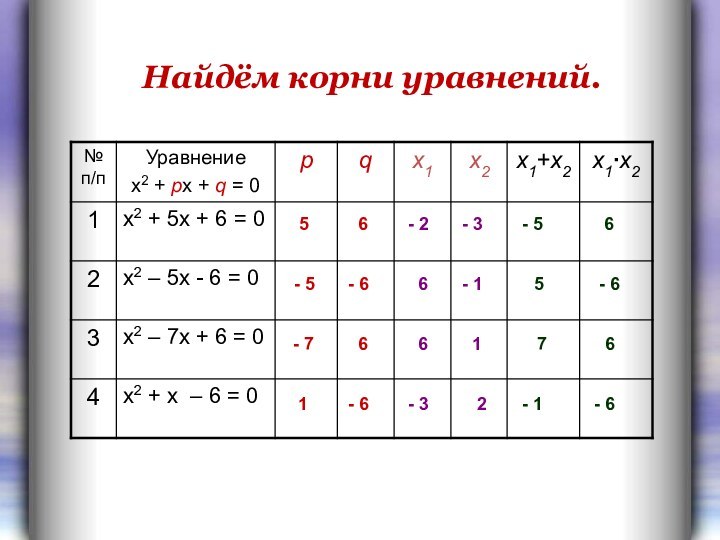
Найдём корни уравнений.

- 2

- 3

6

- 1

6

1

- 3

2

, тогда

Решение:

По теореме, обратной теореме Виета:

Ответ: при q = 8.

Задача: