- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение графов для решения логических задач
Содержание
- 7. Соответствие таблицы и графов
- 8. Ответ: нельзяЗадача1. Между 9 планетами Солнечной
- 9. Определение. Граф называется связным, если две его
- 10. Задача2. В стране Цифра есть 9
- 11. Ответ: нельзяЗадача2 (решение). В стране Цифра есть
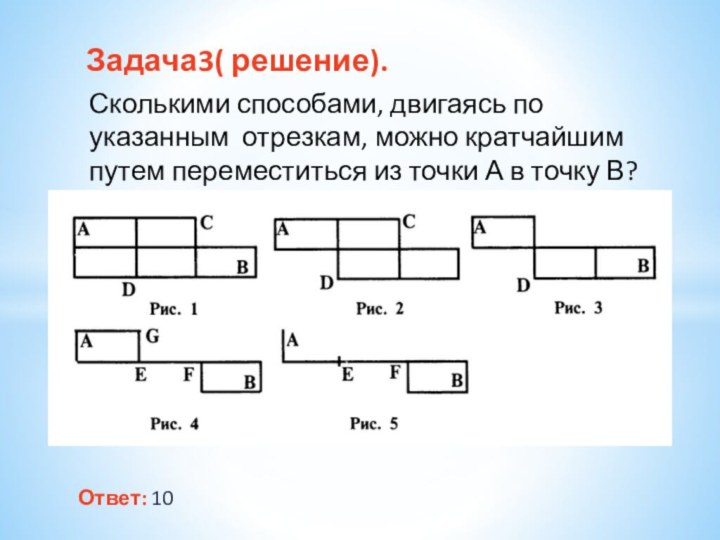
- 12. Задача3. Сколькими способами, двигаясь по указанным
- 13. Ответ: 10Задача3( решение). Сколькими способами, двигаясь
- 14. Задача 4. Пятеро одноклассников – Ирина,
- 15. Ответ. Ирина – победитель олимпиады по математике;
- 16. Задача5. Можно ли поменять коней местами
- 17. Ответ: Коней можно поменять местами минимум за
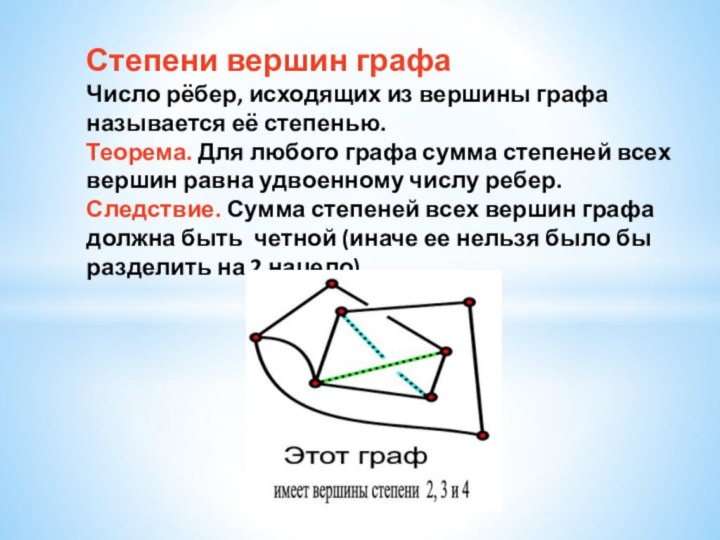
- 18. Степени вершин графа Число рёбер, исходящих
- 19. Задача6. В деревне есть 15 телефонов,
- 20. Четность вершин графа Определение. Вершина графа,
- 21. Задача8. В стране Семерка 15 городов,
- 22. Если добраться нельзя, то граф должен быть
- 23. Задача9. В Тридевятом царстве лишь
- 24. Задача10. Можно ли нарисовать графы, изображенные
- 25. Задача11. Леонард Эйлер, совершая прогулку по
- 26. Задача1. При составлении расписания на понедельник в
- 27. Задача3. Марина, Лариса, Жанна и Катя умеют
- 28. Задача1. Решения: Задача2. Ответ: Андрей –
- 29. Задача3. Решения:
- 30. Задача12( ЕГЭ 2008). Графы в стратегии игр
- 31. Задача12( решение).
- 32. Скачать презентацию
- 33. Похожие презентации






























Слайд 9 Определение. Граф называется связным, если две его вершины
могут быть соединены путем, т. е. последовательностью ребер, каждое
следующее из которых начинается в конце предыдущего.Определение. Несвязный граф состоит из нескольких «кусков».
Эти «куски» называются компонентами связности графа. Каждая компонента несвязного графа является, конечно, связным графом.
Связность графа
Слайд 10 Задача2. В стране Цифра есть 9 городов с
названиями 1, 2, 3, 4, 5, 6, 7, 8,
9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли из города 1 с пересадками добраться в город 9?
Слайд 11
Ответ: нельзя
Задача2 (решение).
В стране Цифра есть 9 городов
с названиями 1, 2, 3, 4, 5, 6, 7,
8, 9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли из города 1 с пересадками добраться в город 9?
Слайд 12
Задача3.
Сколькими способами, двигаясь по указанным отрезкам, можно
кратчайшим путем переместиться из точки А в точку В?
Слайд 13
Ответ: 10
Задача3( решение).
Сколькими способами, двигаясь по указанным
отрезкам, можно кратчайшим путем переместиться из точки А в
точку В?Слайд 14 Задача 4. Пятеро одноклассников – Ирина, Тимур, Камилла,
Эльдар и Захар стали победителями олимпиад школьников по физике,
математике, информати-ке, литературе и географии. Известно, что побе-дитель олимпиады по информатике учит Ирину и Тимура работе на компьютере; Камилла и Эльдар тоже заинтересовались информатикой; Тимур всегда побаивался физики; Камилла, Тимур и победитель олимпиады по литературе занимают-ся плаванием; Тимур и Камилла поздравили победителя олимпиады по математике; Ирина сожалеет о том, что у нее остается мало времени на литературу. Победителем какой олимпиады стал каждый из этих ребят?Слайд 15 Ответ. Ирина – победитель олимпиады по математике; Тимур
– победитель олимпиады по географии; Камилла – победитель олимпиады
по физике; Эльдар – победитель олимпиады по литературе; Захар – победитель олимпиады по информатике.Задача 4 (решение).
Слайд 16 Задача5. Можно ли поменять коней местами и сколько
для этого достаточно ходов? Вершинами графа будут служить занумерованные
клетки, а ребрами- возможные ходы коней.
Слайд 17 Ответ: Коней можно поменять местами минимум за 8
ходов, причем двумя способами
Задача5 (решение).
Можно ли поменять коней местами и сколько для этого достаточно ходов? Вершинами графа будут служить занумерованные клетки, а ребрами- возможные ходы коней.
Слайд 18 Степени вершин графа Число рёбер, исходящих из вершины
графа называется её степенью. Теорема. Для любого графа сумма степеней
всех вершин равна удвоенному числу ребер. Следствие. Сумма степеней всех вершин графа должна быть четной (иначе ее нельзя было бы разделить на 2 нацело).
Слайд 19 Задача6. В деревне есть 15 телефонов, а АТС
отсутствует. Можно ли телефоны соединить проводами так, чтобы каждый
телефон был соединен ровно с пятью другими?
Слайд 20 Четность вершин графа Определение. Вершина графа, имеющая нечетную степень,
называется нечетной, а имеющая четную степень,— четной. Теорема. Число
нечетных вершин любого графа — четно. Задача 7. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 - по 4 друга, а 10 - по 5 друзей. Примечание. Если Петя друг Васи, то Вася - друг Пети.
Слайд 21 Задача8. В стране Семерка 15 городов, каждый из
которых соединен дорогами не менее, чем с 7 другими.
Докажите, что из любого города можно добраться до любого другого (возможно, проезжая через другие города).
Слайд 22 Если добраться нельзя, то граф должен быть несвязным.
Т.К. по условию каждый город должен быть связан минимум
с 7 другими, то городов должно быть не меньше 16, что противоречит условию задачи.Задача8 (решение).
В стране Семерка 15 городов, каждый из которых соединен дорогами не менее, чем с 7 другими. Докажите, что из любого города можно добраться до любого другого (возможно, проезжая через другие города).
Слайд 23 Задача9. В Тридевятом царстве лишь один вид транспорта
— ковер-самолет. Из столицы выходит 21 ковролиния, из города
Дальний — одна, а из всех остальных городов по 20. Докажите, что из столицы можно долететь в Дальний (возможно с пересадками).
Слайд 24 Задача10. Можно ли нарисовать графы, изображенные на рисунках,
не отрывая карандаша от бумаги?
Эйлеровы графы
Слайд 25 Задача11. Леонард Эйлер, совершая прогулку по городу, в
котором он жил, — Кенигсбергу (ныне Калининград), поставил для
себя задачу: прогуляться по всем мостам, перекинутым на два острова реки и между островами так, чтобы по каждому мосту пройти не более одного раза. Представим схему задачи Эйлера:Эйлеровы графы
Задача Эйлера при переводе на язык графов имеет 4 нечетных вершины и, следовательно, не решается.
Слайд 26 Задача1. При составлении расписания на понедельник в IX
классе преподаватели высказали просьбу завучу.
Учитель математики: «Желаю иметь первый
или второй урок».Учитель истории: «Желаю иметь первый или третий урок».
Учитель литературы: «Желаю иметь второй или третий урок».
Какое расписание будет составлено, если по каждому предмету может быть только один урок?
Задача2. На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Мнения девочек разошлись, как места распределились между победителями.
Даша. Андрей был первым, Володя – вторым
Галя. Андрей был вторым, Борис – третьим
Лена. Боря был четвертым, Сережа – вторым.
Ася, которая была судьей на этих соревнованиях, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление. Кто из мальчиков какое место занял?
Решите самостоятельно:
Слайд 27 Задача3. Марина, Лариса, Жанна и Катя умеют играть
на разных инструментах (пианино, виолончели, гитаре, скрипке), но
каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:1.Девушка, которая играет на гитаре говорит на испанском.
2.Лариса не играет ни на скрипке, ни на виолончели и не знает английского языка.
3.Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.
4.Девушка, которая говорит на немецком, не играет на виолончели.
5.Жанна знает французский язык, но не играет на скрипке.
Кто на каком инструменте играет и какой иностранный язык знает?
Решите самостоятельно: