- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Движение в пространстве (11 класс)
Содержание
- 2. Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.
- 3. При движении прямые переходят в прямые, полупрямые
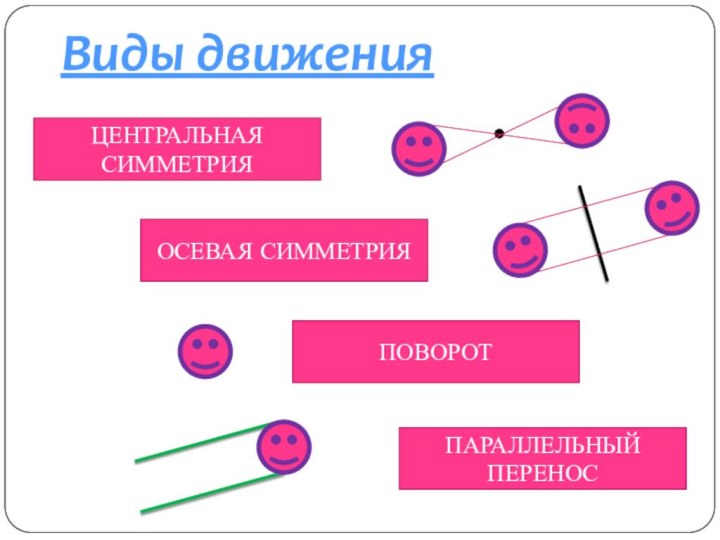
- 4. ОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПОВОРОТПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСВиды движения
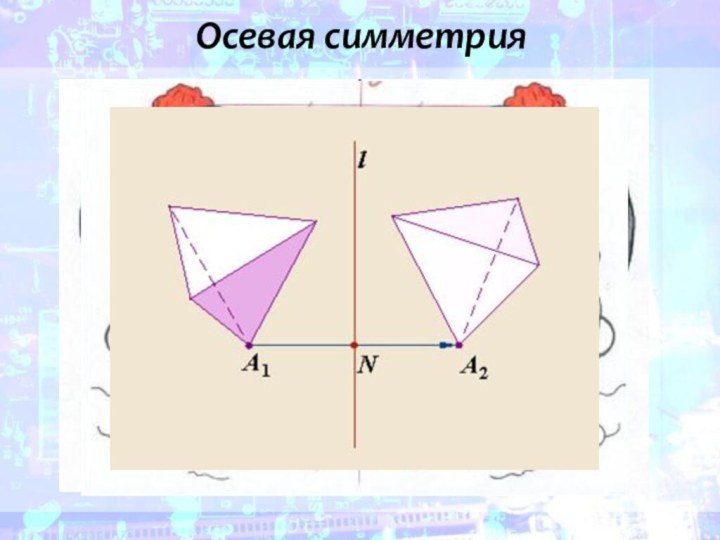
- 5. Осевая симметрия
- 6. Осевой симметрией называют отображение пространства на себя,
- 7. Две точки называются симметричными относительно данной прямой
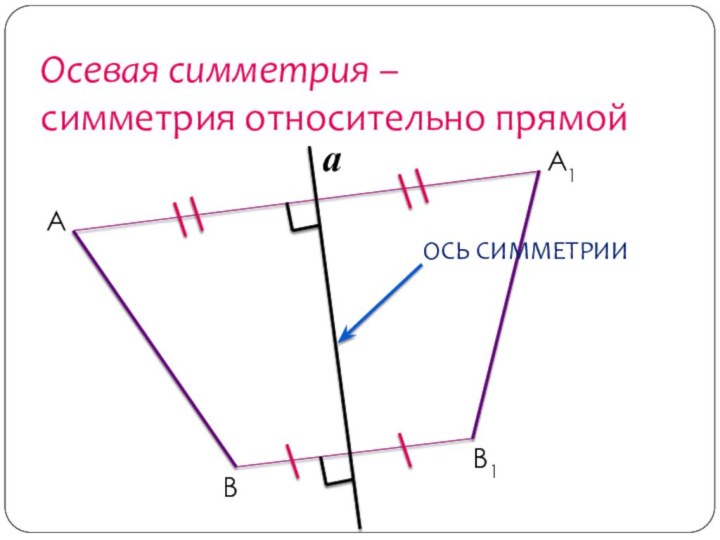
- 8. Осевая симметрия – симметрия относительно прямой АВА1В1a
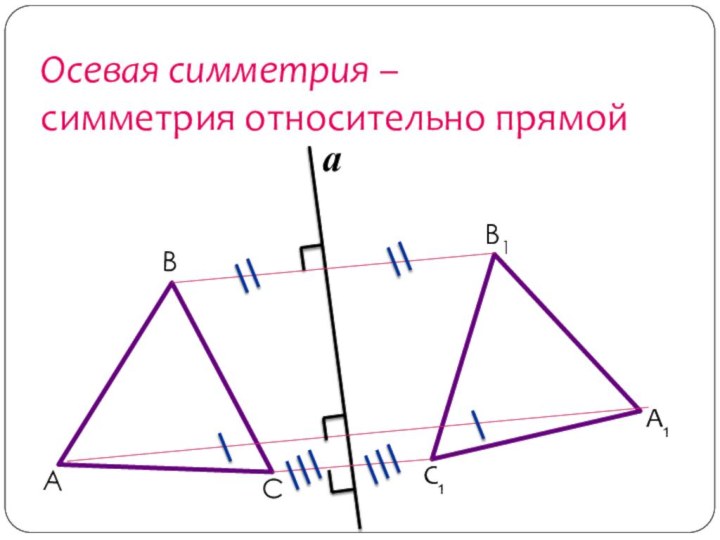
- 9. Осевая симметрия – симметрия относительно прямой С1А1В1a
- 10. Осевая симметрия
- 11. Интересные фактыОднажды в Америке обмерили 72 студента-добровольца.
- 12. Симметрия относительно прямой – двусторонняя симметрияПрисмотритесь
- 13. чтобы построить фигуру, симметричную данной
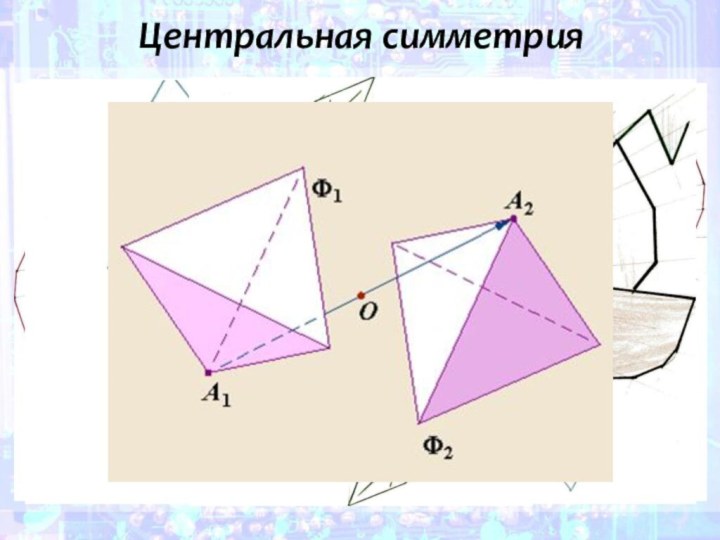
- 14. Центральная симметрия
- 15. Центральной симметрией называют отображение пространства на себя,
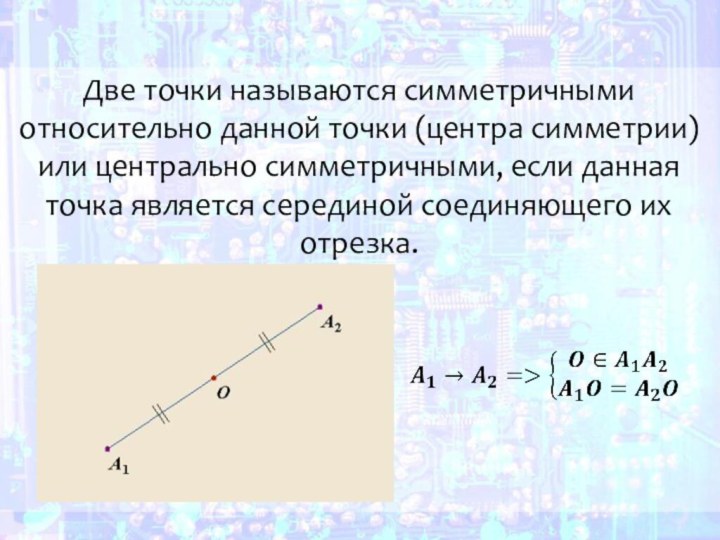
- 16. Две точки называются симметричными относительно данной точки
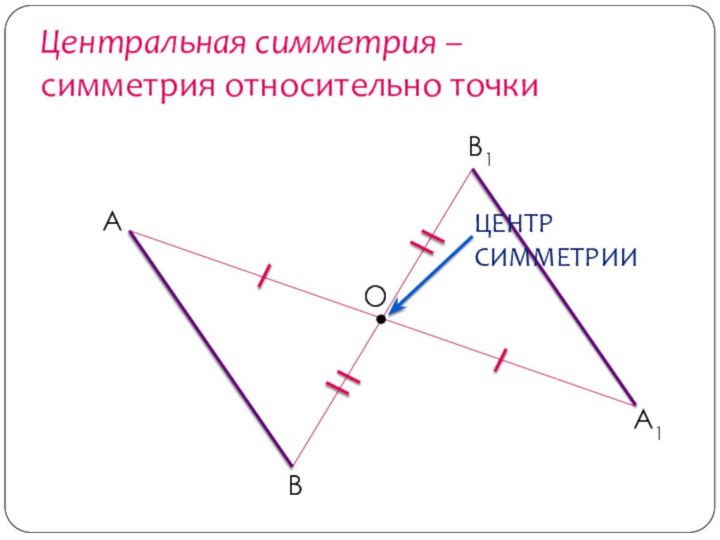
- 17. Центральная симметрия – симметрия относительно точкиА1АВВ1О
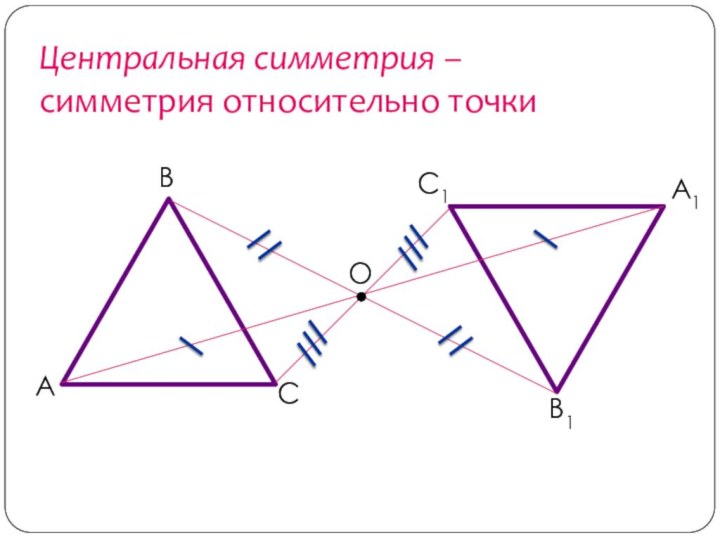
- 18. ОА1В1С1Центральная симметрия – симметрия относительно точки
- 19. Центральная симметрия
- 20. Симметрия относительно точки – лучевая симметрияПрисмотритесь
- 21. чтобы построить фигуру, симметричную данной
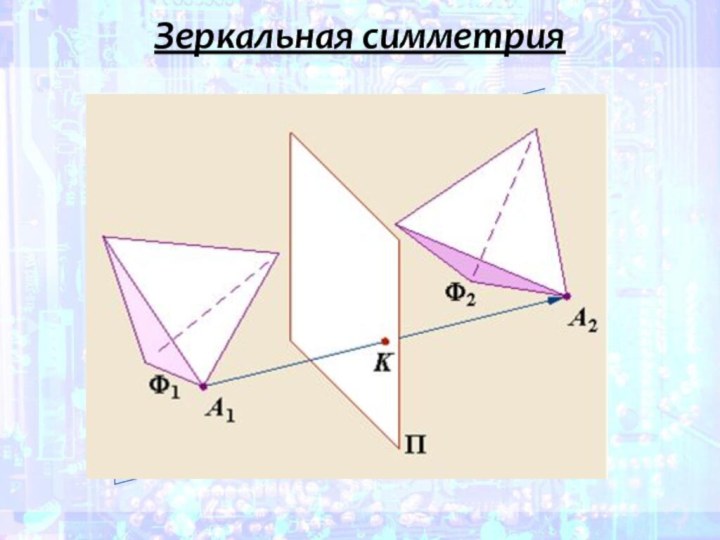
- 22. Зеркальная симметрия
- 23. Зеркальной симметрией (симметрией относительно плоскости α) называется
- 24. Зеркальная симметрия
- 25. Две точки называются симметричными относительно данной плоскости
- 26. ЭкспериментыНапишем на листе бумаги заглавными печатными буквами
- 29. ЭкспериментыЗеркало не подействовало на слово "КОФЕ", тогда
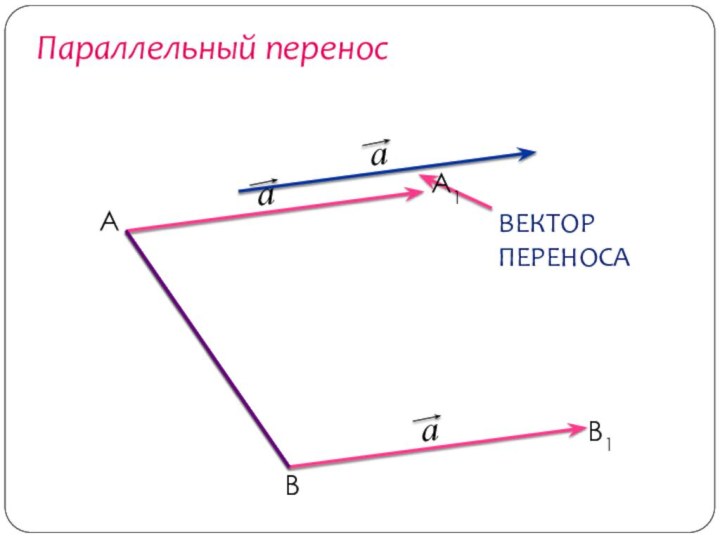
- 30. Параллельный перенос
- 32. Параллельный переносАВА1В1
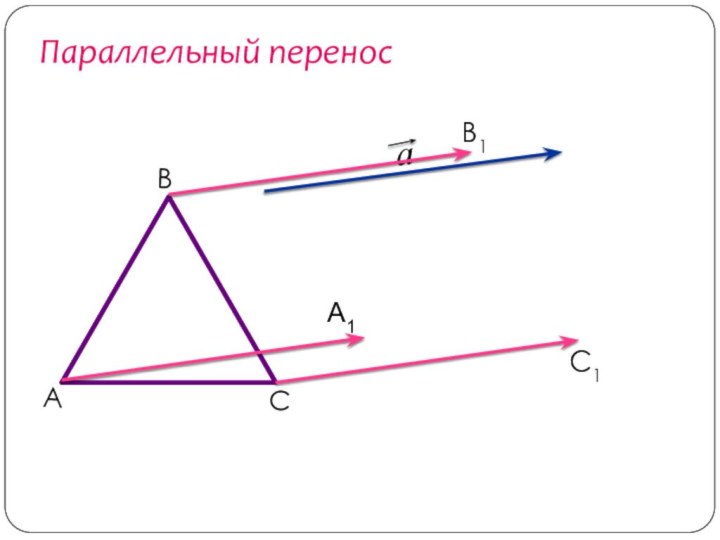
- 33. Параллельный переносС1А1В1САВ
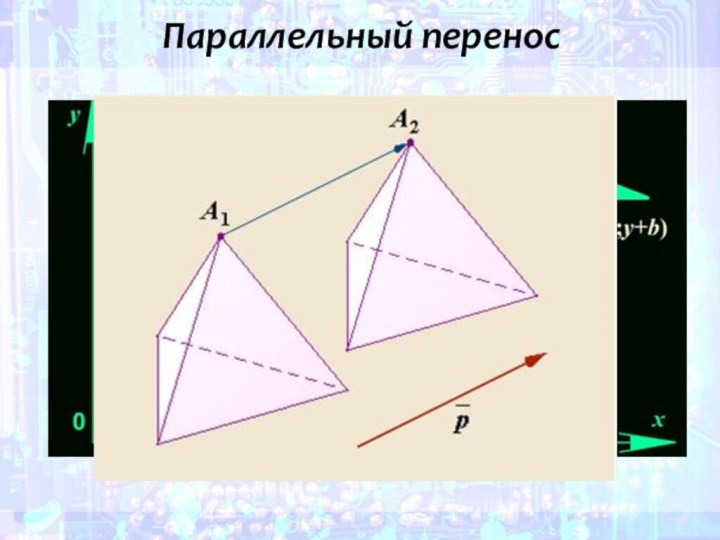
- 34. Параллельный перенос
- 35. Параллельный перенос Сделаем вывод:чтобы отобразить фигуру
- 36. Поворот
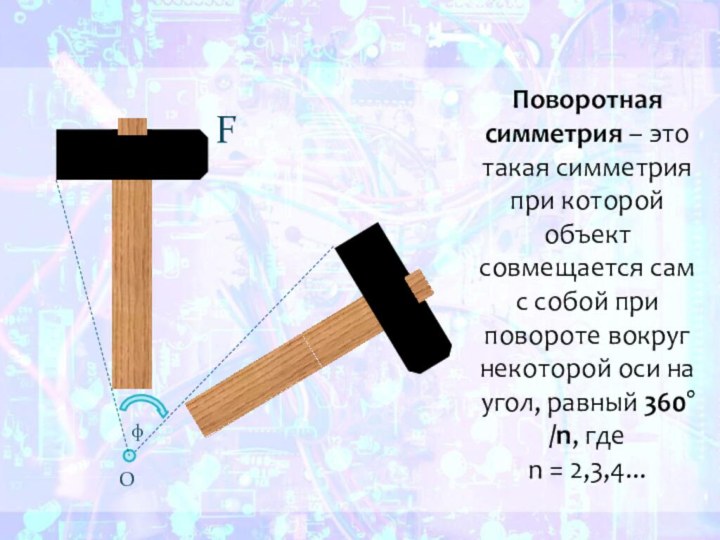
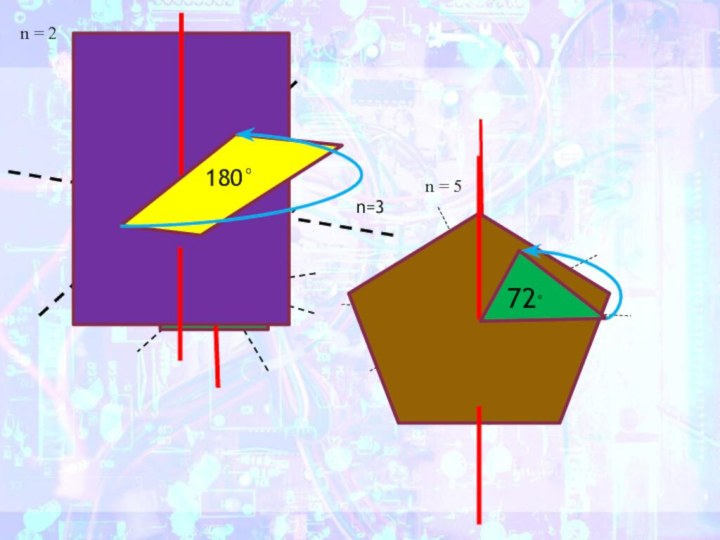
- 37. Поворотная симметрия – это такая симметрия при
- 38. n=3120°n = 490°n = 2180°n = 572°
- 39. При вращении плоскости неподвижная точка называется центром
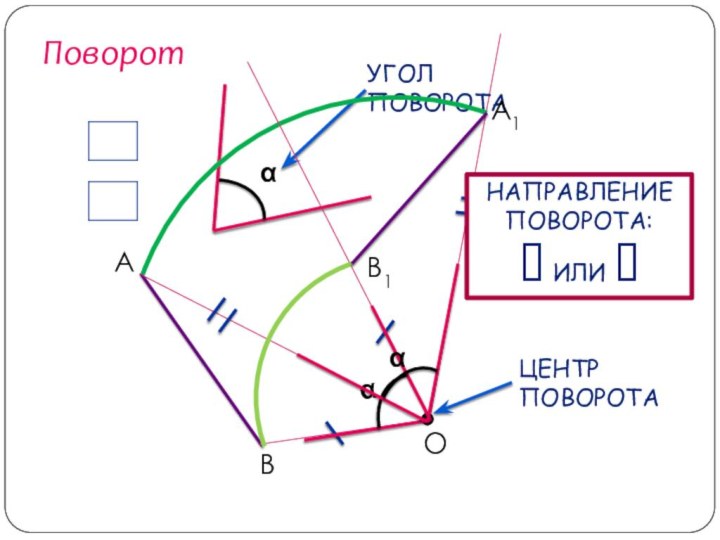
- 40. ПоворотОАВА1В1НАПРАВЛЕНИЕ ПОВОРОТА: ИЛИ
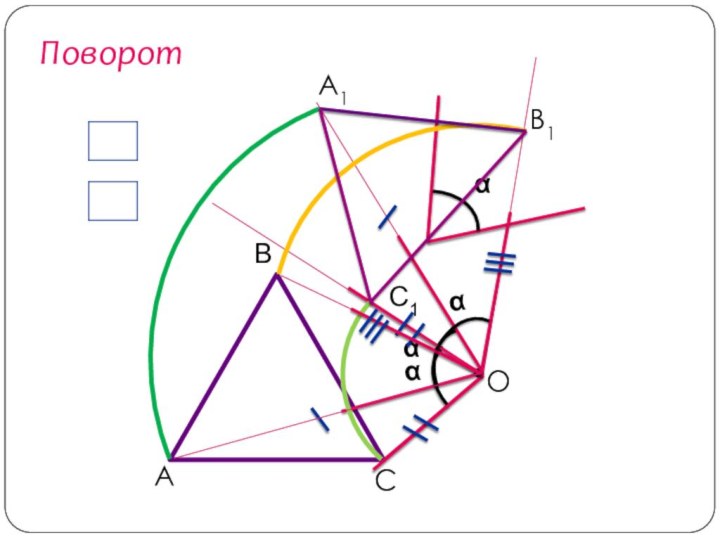
- 41. ПоворотОА1В1С1
- 42. Поворот Сделаем вывод:чтобы получить отображение фигуры
- 43. Гомотетия (преобразование подобия)
- 44. Преобразование плоскости или пространства, при котором фиксированная
- 45. XX1YY1ZZ1UU1OГомотетия
- 46. Композиция движенийКомпозиция – результат последовательного выполнения двух движений.Осевая симметрияПараллельный перенос
- 47. Скачать презентацию
- 48. Похожие презентации
Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.

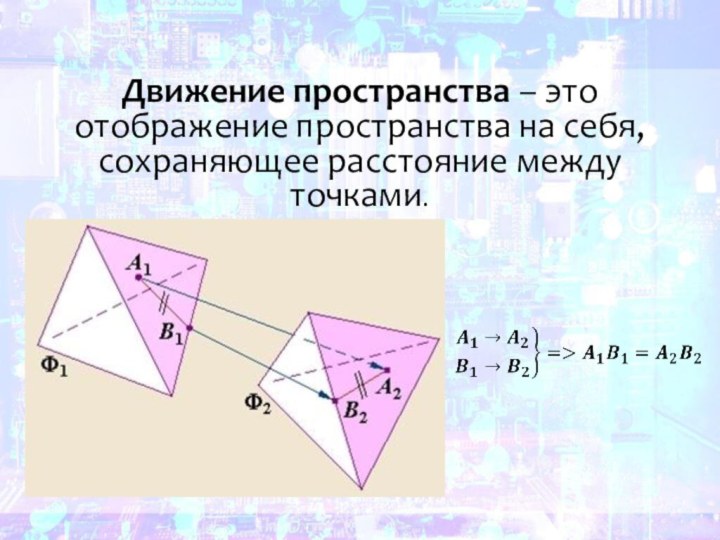



























Слайд 2 Движение пространства – это отображение пространства на себя,
сохраняющее расстояние между точками.
Слайд 3 При движении прямые переходят в прямые, полупрямые –
в полупрямые, отрезки – в отрезки.
Точки, лежащие на
прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.Сохраняются углы между полупрямыми.
Любая фигура переходит в равную ей фигуру
Свойства движения
Слайд 6 Осевой симметрией называют отображение пространства на себя, при
котором любая точка переходит в симметричную ей точку относительно
осиa
Слайд 7 Две точки называются симметричными относительно данной прямой (оси
симметрии), если эта прямая является серединным перпендикуляром соединяющего их
отрезка.
Слайд 11
Интересные факты
Однажды в Америке обмерили 72 студента-добровольца. Данные
подтвердили интуитивно предполагаемый факт: юноши с правильными лицами –
те, у кого отклонения от симметрии не превышали 1 – 2% , были найдены более привлекательными в целом, тогда как менее симметричные студенты – с отклонениями в 5-7% - были признаны менее привлекательными, "некрасивыми" в обычном смысле.
Слайд 12
Симметрия относительно прямой –
двусторонняя симметрия
Присмотритесь внимательно и
вы увидите, что правая сторона – есть зеркальное отображение
левой. В математике – это симметрия относительно прямой (осевая симметрия), в биологии – двусторонняя симметрия.Слайд 13 чтобы построить фигуру, симметричную данной относительно прямой а,
нужно из каждой точки фигуры провести перпендикуляр к прямой
а, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образыОсевая симметрия –
симметрия относительно прямой
Сделаем вывод:
Слайд 15 Центральной симметрией называют отображение пространства на себя, при
котором любая точка переходит в симметричную ей точку относительно
данного центра ОO
F
Слайд 16 Две точки называются симметричными относительно данной точки (центра
симметрии) или центрально симметричными, если данная точка является серединой
соединяющего их отрезка.
Слайд 20
Симметрия относительно точки –
лучевая симметрия
Присмотритесь внимательно и
вы увидите, что лепестки каждого тела расходятся во все
стороны, как лучи от источника света. В математике - это симметрия относительно точки (центральная симметрия), в биологии – лучевая симметрия.Слайд 21 чтобы построить фигуру, симметричную данной относительно точки О,
нужно каждую точку фигуры соединить с точкой О, продолжить
полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образыЦентральная симметрия –
симметрия относительно точки
Сделаем вывод:
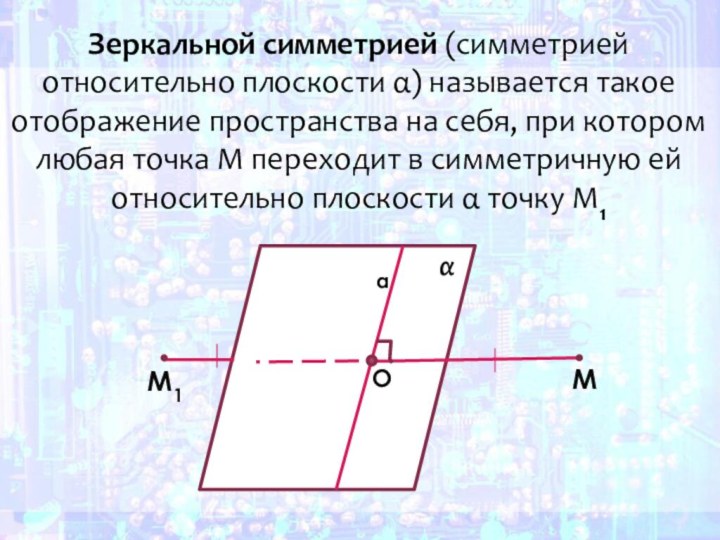
Слайд 23 Зеркальной симметрией (симметрией относительно плоскости α) называется такое
отображение пространства на себя, при котором любая точка М
переходит в симметричную ей относительно плоскости α точку M1М1
M
α
О
а
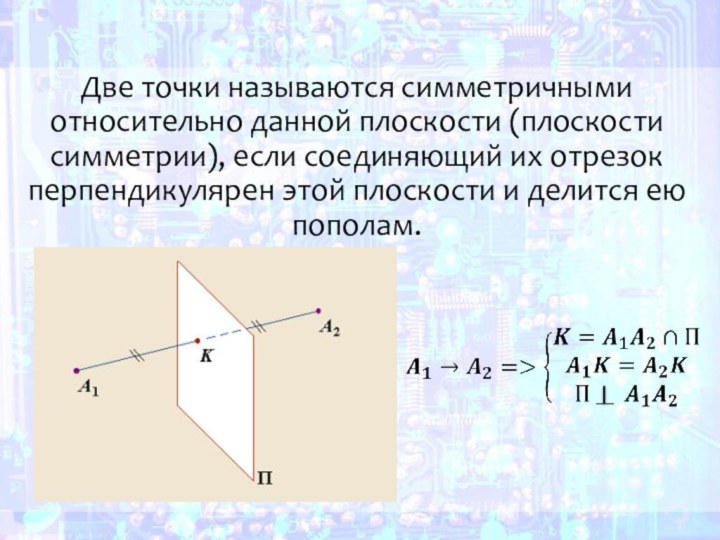
Слайд 25 Две точки называются симметричными относительно данной плоскости (плоскости
симметрии), если соединяющий их отрезок перпендикулярен этой плоскости и
делится ею пополам.
Слайд 26
Эксперименты
Напишем на листе бумаги заглавными печатными буквами два
слова "КОФЕ" и "ЧАЙ". Затем возьмем зеркало и поставим
его вертикально так, чтобы линия пересечения плоскости зеркала с плоскостью листа делила эти слова по горизонтали.
Слайд 29
Эксперименты
Зеркало не подействовало на слово "КОФЕ", тогда как
слово "ЧАЙ" оно изменило до неузнаваемости. Этот "фокус" имеет
простое объяснение. Разумеется, зеркало одинаковым образом отражает нижнюю половину обеих слов. Однако в отличии от слова "ЧАЙ" слово "КОФЕ" обладает горизонтальной осью симметрии, именно поэтому оно не искажается при отражении в зеркале.
Слайд 35
Параллельный перенос
Сделаем вывод:
чтобы отобразить фигуру с помощью параллельного
переноса, нужно каждую точку фигуры переместить на заданный вектор,
а затем соединить полученные образыСлайд 37 Поворотная симметрия – это такая симметрия при которой
объект совмещается сам с собой при повороте вокруг некоторой
оси на угол, равный 360°/n, гдеn = 2,3,4...
F
ф
O
Слайд 39 При вращении плоскости неподвижная точка называется центром вращения,
при вращении пространства неподвижная прямая называется осью вращения (при
этом ось вращения также называется осью поворотной симметрии порядка n).Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).
Слайд 42
Поворот
Сделаем вывод:
чтобы получить отображение фигуры при повороте около
данной точки, нужно каждую точку фигуры повернуть на один
и тот же угол в одном и том же направлении (по часовой стрелке или против часовой стрелки)Слайд 44 Преобразование плоскости или пространства, при котором фиксированная точка
O остается неподвижной, и каждая точка X переходит в
такую точку X1 , что OX1=k OX, где k – заданное число, называется гомотетией.Точка O называется центром гомотетии, k называется коэффициентом гомотетии.
Если фигура F преобразуется в результате гомотетии в фигуру F1 , то фигуры F и F1 называются гомотетичными.





























