- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по решению задач из банка ЕГЭ по теме: Производная, 11 класс
Содержание
- 2. Приветствую вас на уроке Девиз урока:Успешного усвоения учебного материалаУчитесь не мыслям, а мыслитьКвант
- 3. 1.Теория. Глава
- 4. Стр.106, №9(2,4)Найти стационарные точки функциих=7 – стационарная точка функции
- 5. Стр.106, №9(4)Найти стационарные точки функциистационарные точки функции
- 6. Стр.104 учебника.
- 7. Стр.107, №10(2)Раскроем знак модуля при условиях:стационарных
- 8. Стр.107, №10(2)Раскроем знак модуля при условиях:Данная
- 9. Стр.107, №10(4)Раскрываем модуль при условиях:
- 10. Стр.107, №10(3,4)Данная функция не имеет производной
- 11. Стр.107, №11(2,4)Найти точки экстремума функции -
- 12. Стр.107, №11(4)Найти точки экстремума функцииПри переходе
- 13. Стр.107, №12(2,4)Найти точки экстремума функции -
- 14. Стр.107, №12(4)Найти точки экстремума функцииДанная функция
- 15. Стр.107, №14(2)Найти точки экстремума функцииКритические точки: х=0, х=6,25 х=6,25- точка максимума
- 16. Стр.107, №14(4)Найти точки экстремума функцииСтационарные точки: х=-3, х=1 х=-3 точка максимума х=1 точки минимума
- 17. Оцените выполнение ДЗ, проверив его выполнение в парах
- 18. 26.11.18Классная работаПрименение производной при решении заданий ЕГЭ (профиль)Глава III. §1,2.Уроки №45–46
- 19. Цели урока:Рассмотреть задачи профильного ЕГЭ с использованием
- 20. Повторяем теоретический материал: 1. Точки минимума и
- 21. Повторяем теоретический материал: 1. Точки минимума и
- 22. 4. Точки, в которых производная обращается
- 23. 4. Точки, в которых производная обращается
- 24. 6. Если
- 25. 6. Если
- 26. 8. Точка х0 называется точкой максимума
- 27. 8. Точка х0 называется точкой максимума
- 28. 10. Является ли точка х=0
- 29. Стр.107, №14(3)
- 30. Стр.107, №14(3)Раскрываем модуль при условиях:
- 31. Стр.107, №14(3)Раскрываем модуль при условиях: Находим производную каждой функции
- 32. Стр.107, №14(3)Раскрываем модуль при условиях: Находим стационарные точки и знак производной в точке х=5
- 33. Стр.107, №14(3)Раскрываем модуль при условиях: не удовлетворяют условию: Определяем знак производной на промежутках
- 34. Стр.107, №14(3)Раскрываем модуль при условиях: не удовлетворяют условию:
- 36. Подготовка к ЕГЭ. Решение задач на применение производной
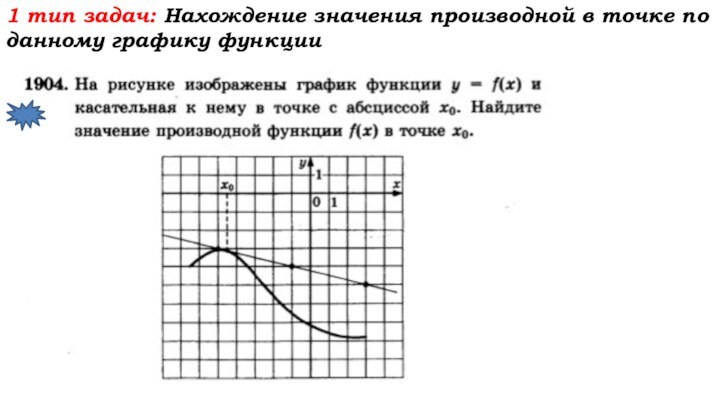
- 37. 1 тип задач: Нахождение значения производной в точке по данному графику функции
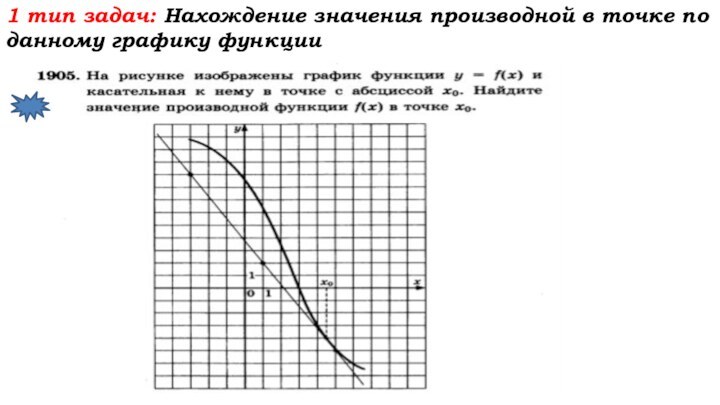
- 38. 1 тип задач: Нахождение значения производной в точке по данному графику функции
- 39. 1 тип задач: Нахождение значения производной в точке по данному графику функции
- 40. 1 тип задач: Нахождение значения производной в точке по данному графику функции
- 41. 1 тип задач: Нахождение значения производной в точке по данному графику функции
- 42. 2 тип задач: Нахождение по данному графику функции количества точек, в которых производная равна 0.
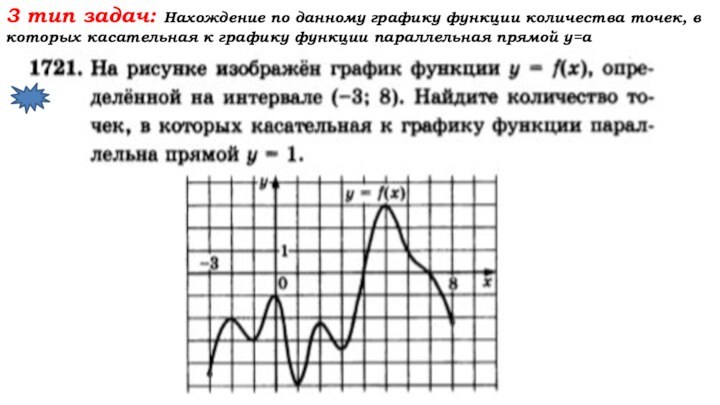
- 43. 3 тип задач: Нахождение по данному графику
- 44. 3 тип задач: Нахождение по данному графику
- 45. 3 тип задач: Нахождение по данному графику
- 46. 3 тип задач: Нахождение по данному графику
- 47. 4 тип задач: Нахождение по данному графику
- 48. 5 тип задач: Нахождение по данному графику
- 49. 5тип задач: Нахождение по данному графику производной
- 50. 5тип задач: Нахождение по данному графику производной
- 51. 5тип задач: Нахождение по данному графику производной
- 52. 5тип задач: Нахождение по данному графику производной
- 53. 5тип задач: Нахождение по данному графику производной
- 54. 5тип задач: Нахождение по данному графику производной
- 55. 6 тип задач: Нахождение количества точек, в
- 56. 6 тип задач: Нахождение количества точек, в
- 57. 6 тип задач: Нахождение количества точек, в
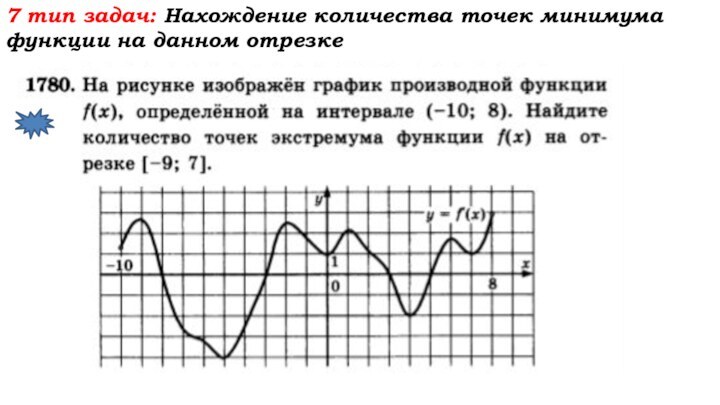
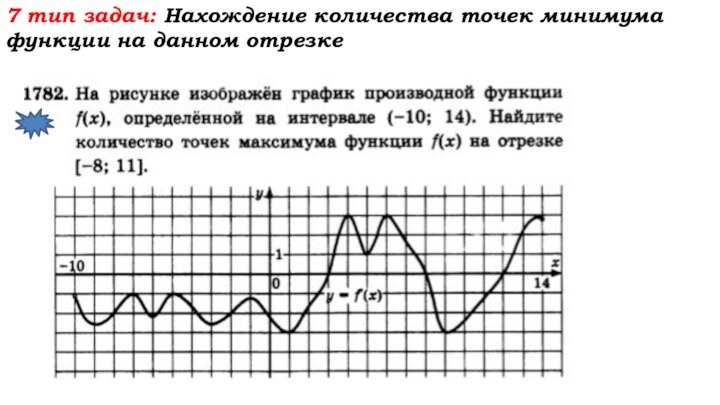
- 58. 7 тип задач: Нахождение количества точек минимума функции на данном отрезке
- 59. 7 тип задач: Нахождение количества точек минимума функции на данном отрезке
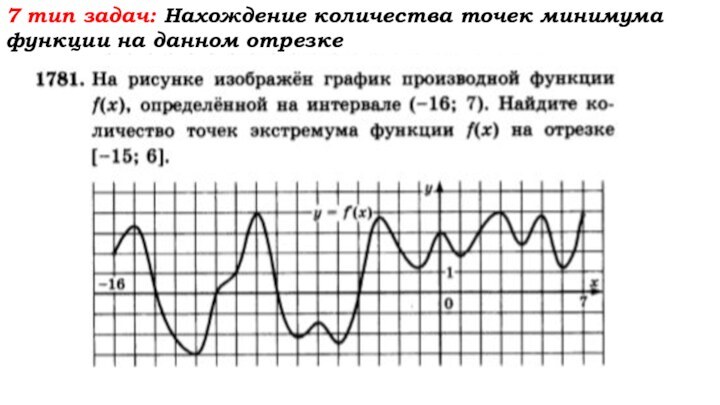
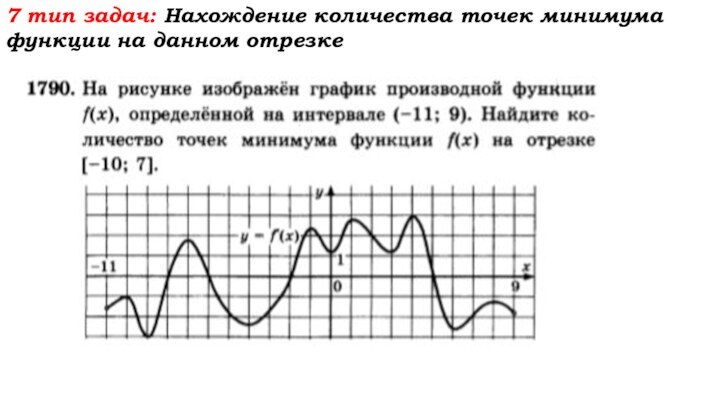
- 60. 7 тип задач: Нахождение количества точек минимума функции на данном отрезке
- 61. 7 тип задач: Нахождение количества точек минимума функции на данном отрезке
- 62. 7 тип задач: Нахождение количества точек минимума функции на данном отрезке
- 63. 7 тип задач: Нахождение количества точек минимума функции на данном отрезке
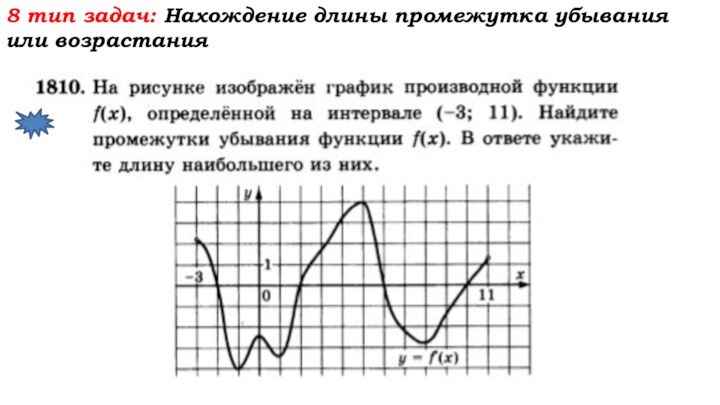
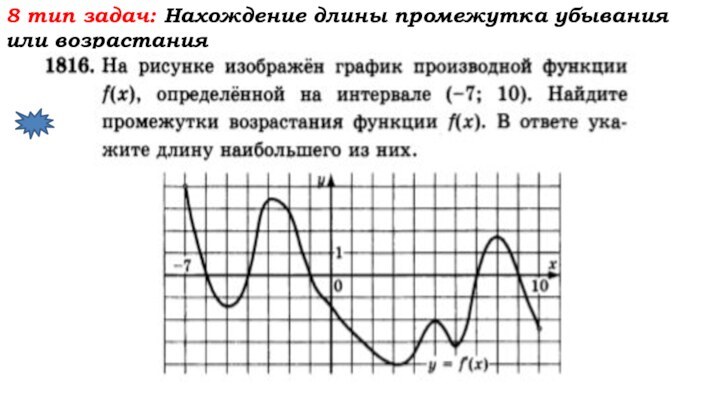
- 64. 8 тип задач: Нахождение длины промежутка убывания или возрастания
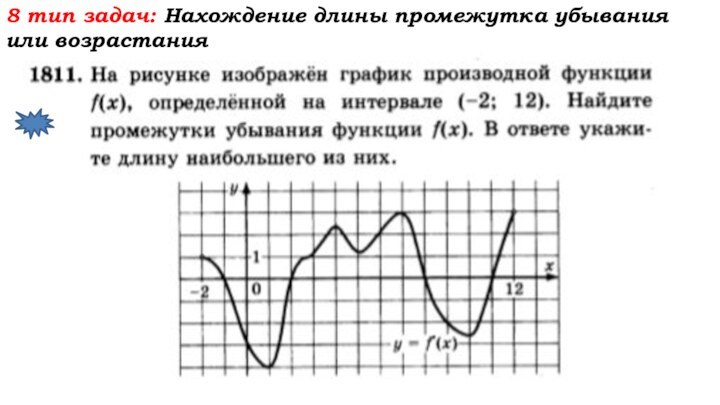
- 65. 8 тип задач: Нахождение длины промежутка убывания или возрастания
- 66. 8 тип задач: Нахождение длины промежутка убывания или возрастания
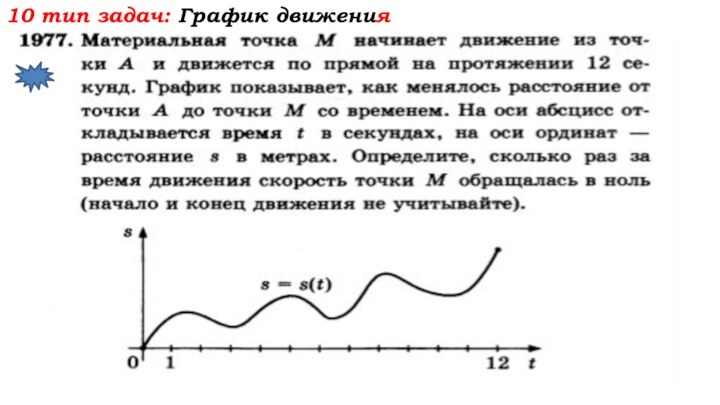
- 67. 10 тип задач: График движения
- 68. 10 тип задач: График движения
- 69. 11 тип задач:Сравнение угловых коэффициентов
- 70. 12 тип задач:Производная положительная и отрицательная
- 71. 12 тип задач:Производная положительная и отрицательная
- 72. 12 тип задач:Производная положительная и отрицательная
- 73. 12 тип задач:Производная положительная и отрицательная
- 74. 12 тип задач:Производная положительная и отрицательная
- 75. 13 тип задач:Найти точку максимума или точку минимума
- 76. 13 тип задач:Найти точку максимума или точку минимума
- 77. 1.Теория. Глава
- 78. Работа по теме: «Производные элементарных функций»_______________________________________
- 79. Скачать презентацию
- 80. Похожие презентации
Приветствую вас на уроке Девиз урока:Успешного усвоения учебного материалаУчитесь не мыслям, а мыслитьКвант


































































Слайд 3
1.Теория. Глава III,
§2
Выучить определения и теоремы §2.
2.Практика. Стр.106-107,
№№9-14 (2,4) ДР№21 на 26.11.18
Слайд 7
Стр.107, №10(2)
Раскроем знак модуля при условиях:
стационарных точек
нет,
т.к.
при
не принадлежат
Слайд 8
Стр.107, №10(2)
Раскроем знак модуля при условиях:
Данная функция
производной в точке х=1 не имеет
Ответ: х=1 – критическая
точка
Слайд 10
Стр.107, №10(3,4)
Данная функция не имеет
производной в
точках х=0 и х=3
Ответ: х=0 и х=3- критические точки
Слайд 11
Стр.107, №11(2,4)
Найти точки экстремума функции
- стационарная
точка функции
При переходе через точку х=-6 производная функции меняет
знак с «-» на «+», поэтому х= -6 – точка минимума
Слайд 12
Стр.107, №11(4)
Найти точки экстремума функции
При переходе через
точку х=-8 производная функции меняет знак с «+» на
«-», поэтомух=-8 – точка максимума, а при переходе через точку х=8 «-» на «+», х=8 – точка минимума
Слайд 13
Стр.107, №12(2,4)
Найти точки экстремума функции
- критическая
точка функции
Данная функция не имеет
производной в точке х=1.
Экстремумов нет
Слайд 14
Стр.107, №12(4)
Найти точки экстремума функции
Данная функция не
имеет
критических точек.
Экстремумов нет
Уравнение не имеет корней
Слайд 15
Стр.107, №14(2)
Найти точки экстремума функции
Критические точки:
х=0,
х=6,25
х=6,25- точка максимума
Слайд 16
Стр.107, №14(4)
Найти точки экстремума функции
Стационарные точки: х=-3,
х=1
х=-3 точка максимума
х=1 точки минимума
Слайд 18
26.11.18
Классная работа
Применение производной при решении заданий
ЕГЭ (профиль)
Глава III. §1,2.
Уроки №45–46
Слайд 19
Цели урока:
Рассмотреть задачи профильного ЕГЭ с использованием производной
к исследованию функции.
Продолжить формирование культуры устной и письменной математической
речи, умения оценивать уровень своих знаний по рассматриваемой теме.
Слайд 20
Повторяем теоретический материал:
1. Точки минимума и точки
максимума называются точками …
2. Если точка х0
– точка экстремума, то
Слайд 21
Повторяем теоретический материал:
1. Точки минимума и точки
максимума называются точками экстремума
2. Если точка х0
–точка экстремума, то Слайд 22 4. Точки, в которых производная обращается в
нуль, называются … … этой функции
5. Внутренняя точка
области определения непрерывной функции , в которой эта функция не имеет производной или имеет производную, равную нулю, называется … … для данной функции Слайд 23 4. Точки, в которых производная обращается в
нуль, называются стационарными точками этой функции
5. Внутренняя точка
области определения непрерывной функции , в которой эта функция не имеет производной или имеет производную, равную нулю, называется критическими точками для данной функции Слайд 24 6. Если при
переходе через точку меняет
знак с
на , то - точка … 7. Если при переходе через точку меняет
знак с на , то - точка …
Слайд 25 6. Если при
переходе через точку меняет
знак с
на , то - точка минимума 7. Если при переходе через точку меняет
знак с на , то - точка максимума
Слайд 26 8. Точка х0 называется точкой максимума функции
, если для всех
из некоторой окрестности , выполняется неравенство 9. Точка х0 называется точкой минимума функции , если для всех из некоторой окрестности , выполняется неравенство
Слайд 27 8. Точка х0 называется точкой максимума функции
, если для всех
из некоторой окружности , выполняется неравенство 9. Точка х0 называется точкой минимума функции , если для всех из некоторой окружности , выполняется неравенство
Слайд 28
10. Является ли точка х=0 критической
точкой данной функции?
11. Является ли точка х=0
точкой экстремума данной функции?
Слайд 32
Стр.107, №14(3)
Раскрываем модуль при условиях:
Находим стационарные
точки и знак производной в точке х=5
Слайд 33
Стр.107, №14(3)
Раскрываем модуль при условиях:
не удовлетворяют
условию:
Определяем знак производной на промежутках
Слайд 42 2 тип задач: Нахождение по данному графику функции
количества точек, в которых производная равна 0.
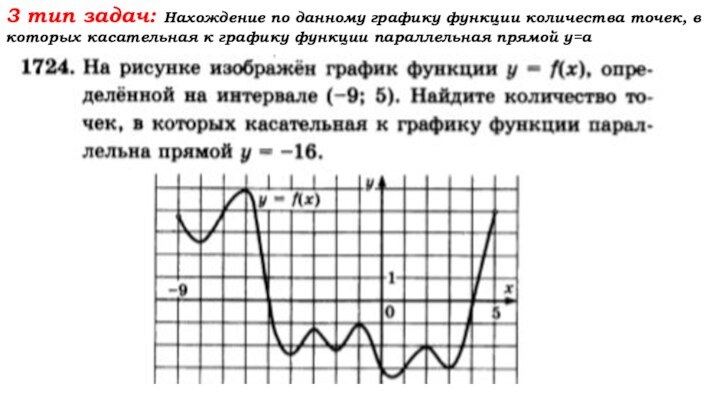
Слайд 43 3 тип задач: Нахождение по данному графику функции
количества точек, в которых касательная к графику функции параллельная
прямой у=аСлайд 44 3 тип задач: Нахождение по данному графику функции
количества точек, в которых касательная к графику функции параллельная
прямой у=аСлайд 45 3 тип задач: Нахождение по данному графику функции
количества точек, в которых касательная к графику функции параллельная
прямой у=аСлайд 46 3 тип задач: Нахождение по данному графику функции
количества точек, в которых касательная к графику функции параллельная
прямой у=аСлайд 47 4 тип задач: Нахождение по данному графику функции
точки, в которых функция принимает наибольшее или наименьшее значение
Слайд 48 5 тип задач: Нахождение по данному графику производной
функции точки, в которых функция принимает наибольшее или наименьшее
значениеСлайд 49 5тип задач: Нахождение по данному графику производной функции
точки, в которых функция принимает наибольшее или наименьшее значение
Слайд 50 5тип задач: Нахождение по данному графику производной функции
точки, в которых функция принимает наибольшее или наименьшее значение
Слайд 51 5тип задач: Нахождение по данному графику производной функции
точки, в которых функция принимает наибольшее или наименьшее значение
Слайд 52 5тип задач: Нахождение по данному графику производной функции
точки, в которых функция принимает наибольшее или наименьшее значение
Слайд 53 5тип задач: Нахождение по данному графику производной функции
точки, в которых функция принимает наибольшее или наименьшее значение
Слайд 54 5тип задач: Нахождение по данному графику производной функции
точки, в которых функция принимает наибольшее или наименьшее значение
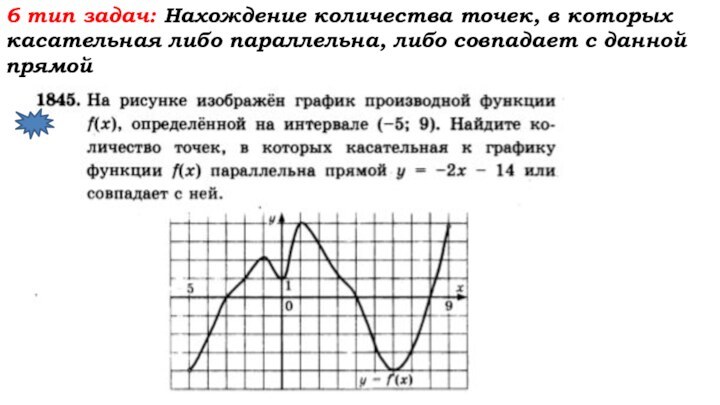
Слайд 55 6 тип задач: Нахождение количества точек, в которых
касательная либо параллельна, либо совпадает с данной прямой
Слайд 56 6 тип задач: Нахождение количества точек, в которых
касательная либо параллельна, либо совпадает с данной прямой
Слайд 57 6 тип задач: Нахождение количества точек, в которых
касательная либо параллельна, либо совпадает с данной прямой
Слайд 77
1.Теория. Глава III,
§2
Выучить определения и теоремы §2.
2.Практика. Сделать
подборку задач (5 задач каждого типа), подобных рассмотренным в классе и решить их
ДР№22 на 30.11.18