- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логарифмы
Содержание
- 2. Содержание 1)Из истории2)Определение логарифма3)Свойства логарифмов4)Виды логарифмов5)Источники информации
- 3. Из истории Джон Не́пер (1550—1617) —
- 4. В ходе тригонометрических расчётов, Неперу пришла в
- 5. В современной записи модель Непера можно изобразить
- 6. Определение логарифма
- 7. Свойства a log a b =
- 8. Формула перехода Log a x = log
- 9. Вещественный логарифмЛогарифм вещественного числа log a b
- 10. Десятичный логарифмЛогарифмы по основанию 10 (обозначение: lg a)
- 11. Подобная шкала широко используется в различных областях науки, например:Физика — интенсивность звука (децибелы).
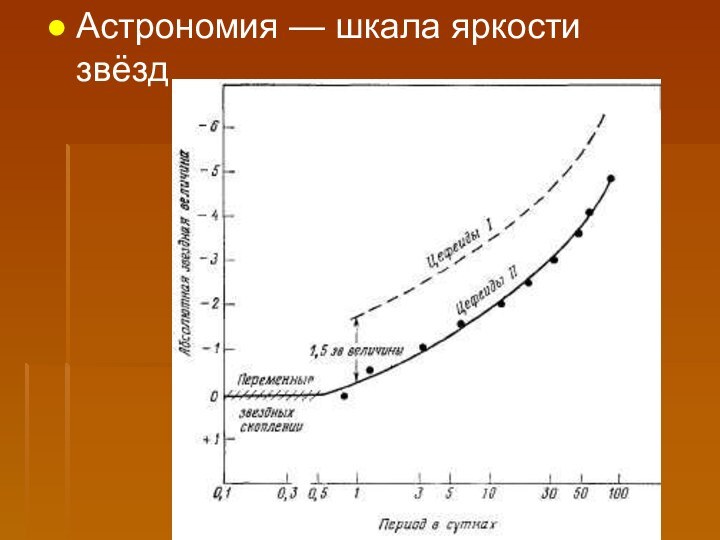
- 12. Астрономия — шкала яркости звёзд
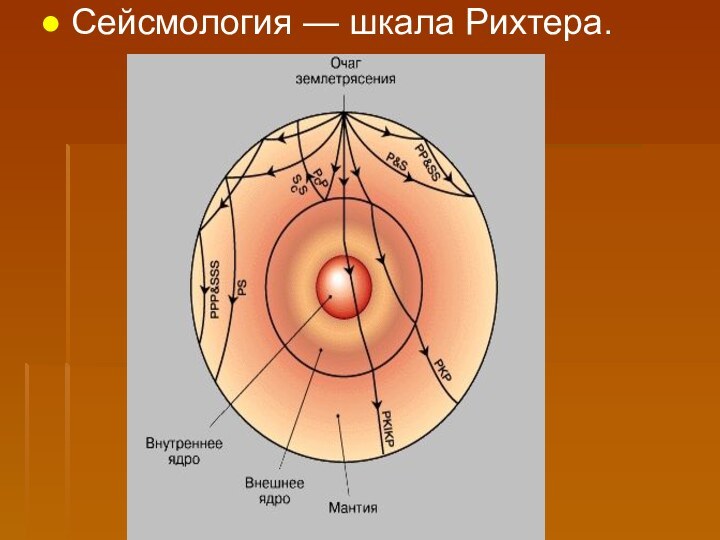
- 13. Сейсмология — шкала Рихтера.
- 14. Теория музыки — нотная шкала, по отношению к частотам нотных звуков.История — логарифмическая шкала времени.
- 15. Химия — активность водородных ионов(pH) Логарифмическая шкала также
- 16. Для рациональных чисел, отличных от 10k с
- 17. Натуральный логарифмЛогарифм по основанию e (e трансцендентное
- 18. Логарифмическая функцияЛогарифмической функцией называется функция вида f(x)
- 19. Скачать презентацию
- 20. Похожие презентации
Содержание 1)Из истории2)Определение логарифма3)Свойства логарифмов4)Виды логарифмов5)Источники информации

















Слайд 2
Содержание
1)Из истории
2)Определение логарифма
3)Свойства логарифмов
4)Виды логарифмов
5)Источники информации
Слайд 4 В ходе тригонометрических расчётов, Неперу пришла в голову
идея: заменить трудоёмкое умножение на простое сложение, сопоставив с
помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание.
Слайд 5
В современной записи модель Непера можно изобразить дифференциальным
уравнением: dx/x = -dy/M, где M — масштабный множитель, введённый
для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом (ln) следующим образом:
LogNap(x) = M * (ln(M) – ln(x))
Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса»есть нуль — этого и добивался Непер своим определением LogNap(0) = ∞
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую.
Слайд 6
Определение логарифма
Логарифмом числа b по основанию a называется показатель степени,в которую нужно возвести основаниеa,чтобы получить число b
Пример log 2 8 = 3
Слайд 7
Свойства
a log a b = b
– основное логарифмическое тождество
Log a a = 1
Log a 1 = 0Log a xy = log a x + log a y
Log a x/y = log a x – log a y
Log a xp= p log a x
Log ak b = 1/k log a b
Log aq bp = p/q log a b
Log ak bk = log a b
Слайд 8
Формула перехода
Log a x = log b
x/log b a
Доказательство
По правилу логарифмирования степени и основному логарифмическому
тождеству получаем Log b x = log b ( a log a x )
Log b x = log a x log b a
Разделив обе части полученного равенства на log b a , приходим к нужной формуле
Слайд 9
Вещественный логарифм
Логарифм вещественного числа log a b имеет
смысл при a>0,a не равное 1,b>0
Наиболее распространённые:
десятичные(основание - 10)
натуральные(основание
е – число Эйлера)двоичные(основание – 2)
Слайд 10
Десятичный логарифм
Логарифмы по основанию 10 (обозначение: lg a) до
изобретения калькуляторов широко применялись для вычислений.
Неравномерная шкала десятичных
логарифмов обычно наносится и на логарифмические линейки.
Слайд 11
Подобная шкала широко используется в различных областях науки,
например:
Физика — интенсивность звука (децибелы).
Слайд 14
Теория музыки — нотная шкала, по отношению к частотам
нотных звуков.
История — логарифмическая шкала времени.
Слайд 15
Химия — активность водородных ионов(pH)
Логарифмическая шкала также широко
применяется для выявления показателя степени в степенных зависимостях и
коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.
Слайд 16 Для рациональных чисел, отличных от 10k с целыми
k, десятичные логарифмы суть трансцендентные числа, которые приближенно выражаются
в десятичных дробях. Целую часть десятичного логарифма называют характеристикой, дробную - мантиссой.Так как lg(10kN) = k + lnN, то десятичные логарифмы чисел, отличающихся множителем 10k, имеют одинаковые мантиссы и различаются лишь характеристиками. Это свойство лежит в основе построения таблиц логарифмов, которые содержат лишь мантиссы логарифмов целых чисел.
Слайд 17
Натуральный логарифм
Логарифм по основанию e (e трансцендентное число,
приближенно равное 2,718281828...) называется натуральным логарифмом.
Натуральный логарифм числа
x обозначается ln x. Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.