параметр а через переменную x
переобозначить координатные оси для работы
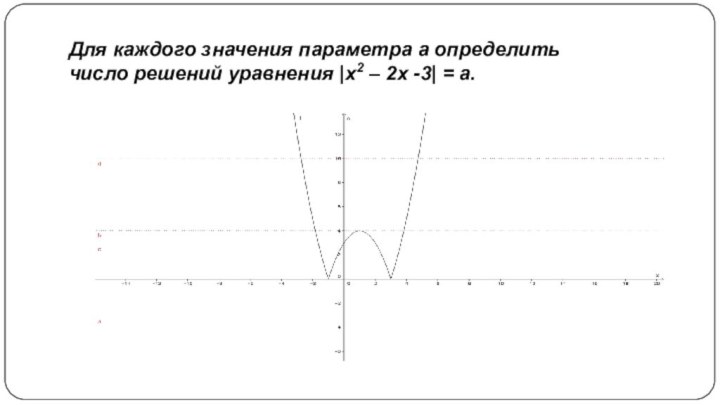
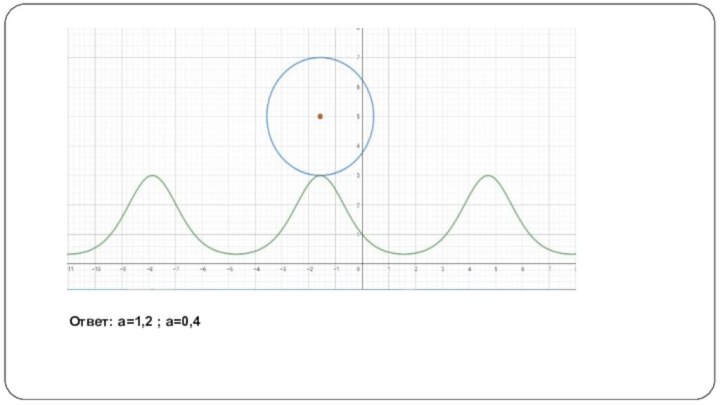
в координатно-параметрической плоскости xОaпостроить графический образ уравнения
пересечь полученный график прямыми, перпендикулярными параметрической оси
записать ответ.