- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Рациональные числа (8 класс)
Содержание
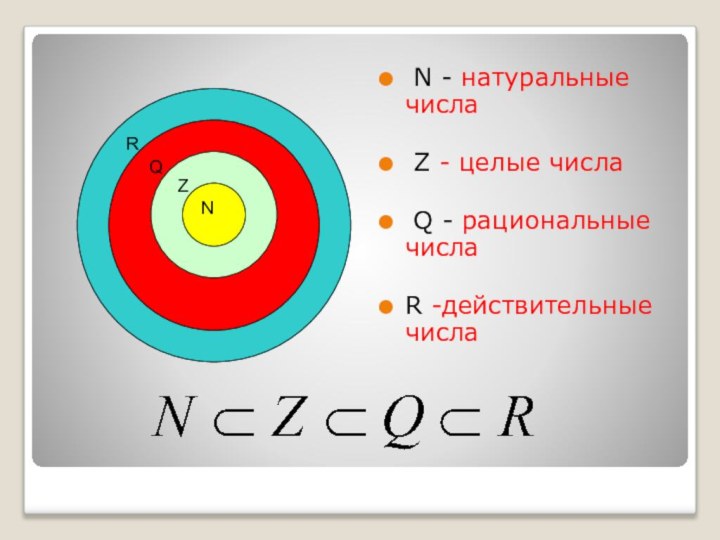
- 2. N - натуральные числа Z - целые числа Q - рациональные числа R -действительные числа
- 4. Целые числаНатуральные числа, противоположные им числа
- 5. Рациональные числаЦелые и дробные числа ( положительные
- 6. 5=5,000000….=5,(0)8,377=8,377…=8,3(7)
- 7. Каждое рациональное число может быть представлено в
- 8. Рациональное число (лат. ratio
- 9. Множество рациональных
- 10. Рациональные числа как бесконечные десятичные дробиДля всех
- 11. Пример. Записать в виде обыкновенной дроби бесконечную
- 12. Положим х=1,5(23)=1,52323…Сначала умножим на 10. Получим 15,2323..,
- 13. Замечание: В примере мы видим, что 0,1(9)=0,2(0).
- 14. Иррациональные числаК иррациональным числам относятся бесконечные десятичные
- 15. Действительные числаМножество действительных чисел состоит из рациональных
- 16. Скачать презентацию
- 17. Похожие презентации
N - натуральные числа Z - целые числа Q - рациональные числа R -действительные числа














Слайд 3
Натуральные числа
Числа 1, 2,
3, …, употребляемые при счете предметов, образуют множество натуральных чисел. Обозначают буквой N.
Например, запись 27Є N читается: «27 принадлежит множеству натуральных чисел».
Любое натуральное число в десятичной системе счисления записывается с помощью цифр 0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9.
Например, запись 2457 означает, что 2457=2•1000+4•100+5•10+7.
Вообще если а - цифра тысяч, b –цифра сотен, d- цифра десятков и c- цифра единиц то имеем а • 1000+b•100+c•10+d.
Используется также сокращенная запись аbcd.
Слайд 4
Целые числа
Натуральные числа, противоположные им числа и
число нуль Составляют множество целых чисел.
Обозначают буквой Z.
Например, запись -27Є Z читается: «-27 принадлежит множеству целых чисел».
Слайд 5
Рациональные числа
Целые и дробные числа ( положительные и
отрицательные ) составляют множество рациональных чисел.
Обозначают буквой Q. Например, запись -3,5Є Q читается: «-3.5 принадлежит множеству рациональных чисел».
Всякое рациональное число можно представить в виде дроби, m/n, где m Є Z, n Є N. Например: 5=5/1=10/2=15/3, 0,7=7/10, -4=-4/1.
Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Например:
5 8,377
-0,5
Слайд 7 Каждое рациональное число может быть представлено в виде
конечной десятичной дроби или бесконечной десятичной периодической дроби.
Слайд 8 Рациональное число (лат. ratio —
отношение, деление, дробь) — число, представляемое обыкновенной дробью ,
где числитель m — целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся. В реальной жизни рациональные числа используются для счёта частей некоторых целых, но делимых объектов, например, тортов или других продуктов, разрезаемых на несколько частей
Слайд 9
Множество рациональных чисел
Множество рациональных чисел обозначается и может быть записано
в виде:Нужно понимать, что численно равные дроби
такие как, например, и , входят в это множество как
одно число. Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
Слайд 10
Рациональные числа как бесконечные десятичные дроби
Для всех рациональных
чисел можно использовать один и тот же способ записи.
Рассмотрим1. Целое число 5
5,000
2. Обыкновенную дробь
0, 3(18)
3. Десятичную дробь 8,377
8,3(7)
Слайд 11 Пример. Записать в виде обыкновенной дроби бесконечную десятичную
периодическую дробь.
Положим, что х=1,(23), т.е. 1,232323…
100х=123,2323…
100х=123,2323…
х=1,2323…99х=122
х=
Итак: 1,(23)=
Слайд 12
Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а
потом ещё на 100
1000х=1523,2323…
10х= 15,232323…
990х=1508х=
Итак: 1,5(23)=
Слайд 13 Замечание: В примере мы видим, что 0,1(9)=0,2(0). Аналогично
можно установить, что 2,45(9)=2,46(0) и т.д. Поэтому обычно десятичные
дроби с периодом 9 не рассматриваются, заменяют их соответственно дробями с периодом 0.Пусть х=0,1(9), тогда
100х=19,999…
-10х= 1,999…
90х=18
Итак, х=0,1(9)= = , но
= 0,2
Слайд 14
Иррациональные числа
К иррациональным числам относятся бесконечные десятичные непериодические
дроби. Например: 3,01001…,
π ≈ 3,145926…,
√2 ≈1,4…√3
≈1,7
Слайд 15
Действительные числа
Множество действительных чисел состоит из рациональных и
иррациональных чисел.
Обозначают буквой R. Например,
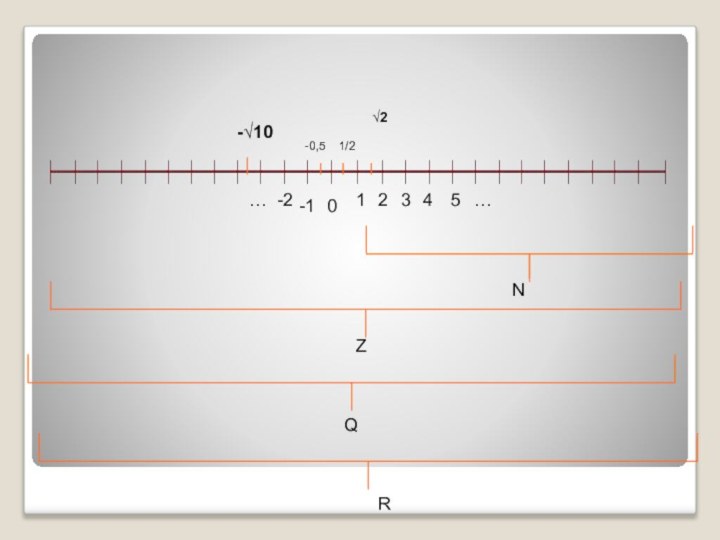
запись -3,5Є R читается: «-3.5 принадлежит множеству действительных чисел».Множество действительных чисел называют также числовой прямой. Каждой точке координатной прямой соответствует некоторое действительное число, и каждому действительному числу соответствует точка на координатной прямой.
К иррациональным числам относятся бесконечные десятичные непериодические дроби. Например: 3,01001…, π ≈ 3,145926…,
√2 ≈1,4.
-√2
√2
0,5





























