Презентация на тему по математике на тему Комплексные числа

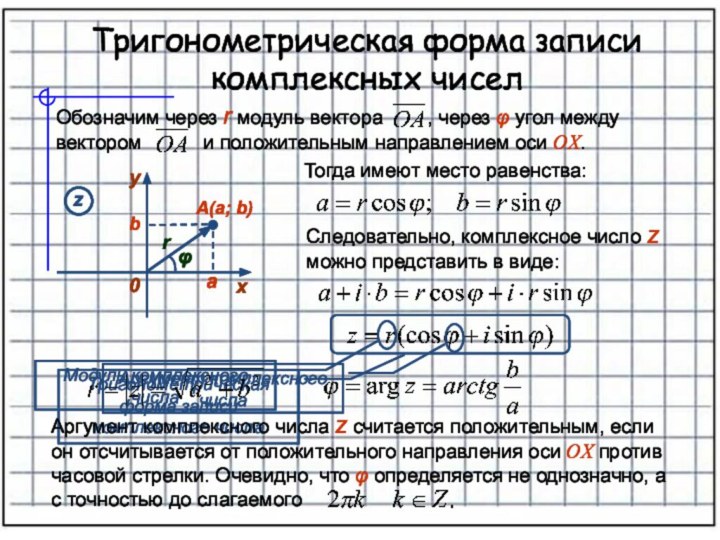
b – действительные числа, i – мнимая единица, определяемая

а называется действительной частью числа z,
b – мнимой частью.

Если а = 0, то число i b называется чисто мнимым.
Если b = 0, то получается действительное число а.

Два комплексных числа, отличающиеся только знаком мнимой части, называются сопряженными:

числа, называют плоскостью комплексной переменной.
A(a; b)
a
b
Точкам, лежащим на оси

Точкам, лежащим на оси OY , соответствуют чисто мнимые числа (a = 0), поэтому ось OY называют мнимой осью.

Действия над

При любом целом k:

3

Сложение и вычитание комплексных чисел.

сопряженных комплексных чисел:
Умножение комплексных чисел.
4

Умножением комплексных чисел и
называется число, получаемое при умножении этих чисел по правилам алгебры как двучлены

Деление комплексных

чисел:

комплексное число z можно представить в виде:
φ
Тригонометрическая форма

Аргумент комплексного числа z считается положительным, если он отсчитывается от положительного направления оси OX против часовой стрелки. Очевидно, что φ определяется не однозначно, а с точностью до слагаемого

r

Умножение комплексных чисел в тригонометрической форме.
1

Если комплексные числа заданы в тригонометрической форме:

тогда произведение находится по формуле:

2

Деление комплексных чисел в тригонометрической форме.

Если комплексные числа заданы в тригонометрической форме:

то деление находится по формуле:

Возведение в степень комплексного числа.

4

Извлечение корня из комплексного числа.

2, …,n –1, получим n различных значений корня.
Итак, корень

из единицы
A
В
С

тригонометрической форме::
Всякое комплексное число можно представить в показательной

Действия над комплексными числами в показательной форме:

Пусть имеем:

Тогда: