Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Определение производной

Содержание

Производной функции y=f(x) называется предел отношения приращения функции к приращениюнезависимого аргумента, когдаприращение аргумента стремитсяк нулю:
8.2. Определение производнойПусть функция y=f(x) определена на промежутке Х. Выберем точку Дадим Производной функции y=f(x) называется предел отношения приращения функции к приращениюнезависимого аргумента, когдаприращение аргумента стремитсяк нулю: Обозначения производной:Нахождение производной функции называетсядифференцированием.Если функция имеет конечную производную в некоторой точке, Вернемся к рассматриваемым задачам.Из задачи о касательной вытекаетПроизводная f / (x0) есть Тогда уравнение касательной к кривой в данной точке будет иметь вид: Из задачи о скорости движения вытекаетПроизводная пути по времени S / (t0) Производная объема производимой продукции по времени u / (t0) есть производительность труда ПРИМЕР.График функции y=f(x) есть полуокружность.Найти f / (x) в точках A,B,C,D,E, делящихполуокружность на четыре равные части. Из геометрического смысла производной вытекает, что производная f / (x0) есть тангенс В точке С угол касательная параллельна оси х:В точках А и Е ТЕОРЕМАЕсли функция y=f(x) дифференцируема в точке x0, то она непрерывна в этойточке. Доказательство:По условию теоремы функция y=f(x) дифференцируема в точке x0 :На основании теоремы где α(Δx) – бесконечно малая величина при Отсюда:При и Следовательно, по определению Обратная теорема, в общем случае, неверна.Например, функциянепрерывна в точке x=0:Проверим, будет ли Т.е. общего предела не существует и функция не дифференцируема в этой точке. Непрерывность функции является необходимым, но не достаточным условием дифференцируемости функции.Если функция имеет
Слайды презентации

Слайд 2 Производной функции y=f(x)
называется предел отношения
приращения функции

Производной функции y=f(x) называется предел отношения приращения функции к приращениюнезависимого аргумента, когдаприращение аргумента стремитсяк нулю:

к приращению
независимого аргумента, когда
приращение аргумента стремится
к нулю:


Слайд 3
Обозначения производной:
Нахождение производной функции называется
дифференцированием.
Если функция имеет конечную

Обозначения производной:Нахождение производной функции называетсядифференцированием.Если функция имеет конечную производную в некоторой

производную в
некоторой точке, то она называется
дифференцируемой в

этой точке.


Слайд 4 Вернемся к рассматриваемым задачам.
Из задачи о касательной вытекает

Производная

Вернемся к рассматриваемым задачам.Из задачи о касательной вытекаетПроизводная f / (x0)

f / (x0) есть угловой коэффициент (тангенс угла наклона)

касательной, проведенной к кривой y=f(x) в точке x0 :




геометрический смысл производной:

Слайд 5 Тогда уравнение касательной к кривой в данной точке

Тогда уравнение касательной к кривой в данной точке будет иметь вид:

будет иметь вид:


Слайд 6 Из задачи о скорости движения вытекает

Производная пути по

Из задачи о скорости движения вытекаетПроизводная пути по времени S /

времени S / (t0) есть скорость точки в момент

времени t0 :




механический смысл производной:

Слайд 7
Производная объема производимой продукции по времени u /

Производная объема производимой продукции по времени u / (t0) есть производительность

(t0) есть производительность труда в момент времени t0 :


Из задачи о производительности труда вытекает




экономический смысл производной:

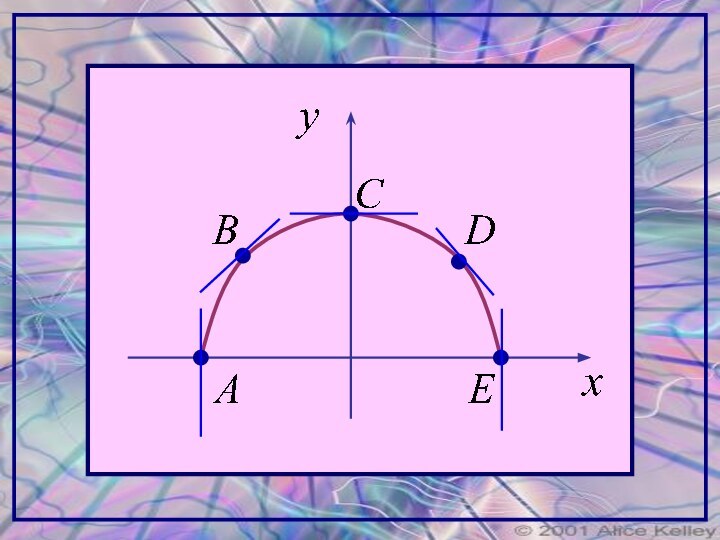
Слайд 8 ПРИМЕР.
График функции y=f(x) есть полуокружность.
Найти f / (x)

ПРИМЕР.График функции y=f(x) есть полуокружность.Найти f / (x) в точках A,B,C,D,E, делящихполуокружность на четыре равные части.

в точках A,B,C,D,E, делящих
полуокружность на четыре равные части.

Слайд 9







Слайд 10 Из геометрического смысла производной вытекает, что производная f

Из геометрического смысла производной вытекает, что производная f / (x0) есть

/ (x0) есть тангенс угла наклона касательной, проведенной к

кривой y=f(x) в точке x0 .

В точке В угол наклона касательной составляет 450. Следовательно:

В точке D угол наклона касательной составляет 1350. Следовательно:


Слайд 11 В точке С угол касательная параллельна оси х:
В

В точке С угол касательная параллельна оси х:В точках А и

точках А и Е угол наклона касательной составляет 900.


Тангенс этого угла не существует, следовательно функция в этих точках не дифференцируема.


Слайд 12 ТЕОРЕМА
Если функция y=f(x)
дифференцируема в точке x0,
то

ТЕОРЕМАЕсли функция y=f(x) дифференцируема в точке x0, то она непрерывна в этойточке.

она непрерывна в этой
точке.

Слайд 13 Доказательство:
По условию теоремы функция y=f(x) дифференцируема в точке

Доказательство:По условию теоремы функция y=f(x) дифференцируема в точке x0 :На основании

x0 :
На основании теоремы о связи бесконечно малых величин

с пределами функций функцию, стоящую под знаком предела, можно представить как сумму этого предела и бесконечно малой величины:


Слайд 14 где α(Δx) – бесконечно малая величина при
Отсюда:
При

где α(Δx) – бесконечно малая величина при Отсюда:При и Следовательно, по


и
Следовательно, по определению непрерывности функции, функция y=f(x) непрерывна

в точке x0.



Слайд 15 Обратная теорема, в общем случае, неверна.
Например, функция
непрерывна в

Обратная теорема, в общем случае, неверна.Например, функциянепрерывна в точке x=0:Проверим, будет

точке x=0:
Проверим, будет ли эта функция дифференцируема в данной

точке.


Слайд 16 Т.е. общего предела не существует и функция не

Т.е. общего предела не существует и функция не дифференцируема в этой точке.

дифференцируема в этой точке.

  • Имя файла: opredelenie-proizvodnoy.pptx
  • Количество просмотров: 142
  • Количество скачиваний: 0
- Предыдущая Правописание безударных личных окончаний глагола
Следующая - создание рисунков в текстовом редакторе

Похожие презентации

Урок-путешествие в страну Дроби. 5-й класс Урок-путешествие в страну Дроби. 5-й класс 151
Комплексные числа Комплексные числа 180
Дидактическая игра Точно в цель на тему Поворот точки вокруг начала координат -2 Дидактическая игра Точно в цель на тему Поворот точки вокруг начала координат -2 143
Натуральные логарифмы Натуральные логарифмы 161
Презентация к уроку по алгебре 7 класс. Тема: Прямая пропорциональность. Презентация к уроку по алгебре 7 класс. Тема: Прямая пропорциональность. 153
Презентация по математике Преобразование графиков функций (8 класс) Презентация по математике Преобразование графиков функций (8 класс) 173
Урок по математике для 8 класс (урок рефлексии) по теме Квадратные уравнения+ презентация Урок по математике для 8 класс (урок рефлексии) по теме Квадратные уравнения+ презентация 183
Предел функции в бесконечности и в точке Предел функции в бесконечности и в точке 194
Презентация по математике на тему Тригонометрические уравнения. ОТбор корней в тринометрических уравнениях (11 класс) Презентация по математике на тему Тригонометрические уравнения. ОТбор корней в тринометрических уравнениях (11 класс) 95
Типы иррациональных уравнений Типы иррациональных уравнений 152
Первообразная Первообразная 162
Өрнектерді түрлендіруде негізгі тригонометриялық тепе – теңдікті қолдану Өрнектерді түрлендіруде негізгі тригонометриялық тепе – теңдікті қолдану 216
Повторяем математику Повторяем математику 340
Материалы к занятию. Алгебра комбинаторика. Материалы к занятию. Алгебра комбинаторика. 174
Решение задач на исследование функций с помощью производной Решение задач на исследование функций с помощью производной 158
Логарифмы Логарифмы 186
Степень и её свойства Степень и её свойства 238
Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем показателем Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем показателем 151
Презентация программы элективного курса по математике на тему Проценты (9 класс) Презентация программы элективного курса по математике на тему Проценты (9 класс) 157
Примеры неравенств Примеры неравенств 195
Неопределенный интеграл Неопределенный интеграл 145
График линейной функции График линейной функции 137
Презентация по алгебре Квадратные уравнения (8 класс) Презентация по алгебре Квадратные уравнения (8 класс) 176
: Линейная функция и ее графики 7 класс : Линейная функция и ее графики 7 класс 177
Алгебра логики. Понятие высказывания Алгебра логики. Понятие высказывания 149
Функция у=кх2 ,ее свойства и график Функция у=кх2 ,ее свойства и график 171
2016 год: ЛегоМатематика. Лекция для учителей математики 2016 год: ЛегоМатематика. Лекция для учителей математики 136
Презентация по математике на тему Арифметическая прогрессия Презентация по математике на тему Арифметическая прогрессия 142
Презентация по математике для внеклассного мероприятия Математический бой. (7-8 класс) Презентация по математике для внеклассного мероприятия Математический бой. (7-8 класс) 220
ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКЕ ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКЕ ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ 165