Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Понятие комбинаторики

Содержание

3. Цели и задачиЗнакомство с новым разделом математикиРассмотреть все тонкости этого разделаНаучиться решать задачи по комбинаторике
4. Комбинаторика очень нужный и сложный раздел математики.
5. КОМБИНАТОРИКА – область математики, в которой изучаются
6. ГРАФ – совокупность объектов со связями между
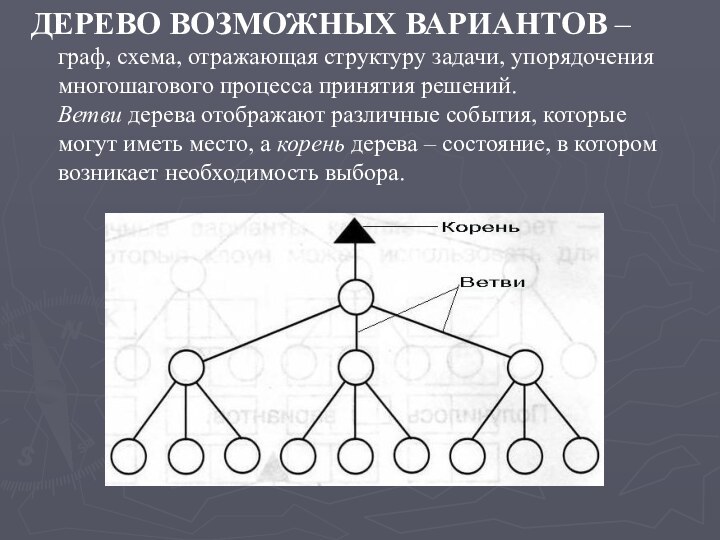
7. ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ – граф, схема, отражающая
8. КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления
9. Из чисел 1, 5, 9 составить трёхзначное
10. Пример 2 Сколько двузначных чисел можно составить,
11. 1 Правило суммы:n(AυB)=n(A)+n(B), n-мощность множествn(A) - число
12. n(A*B)=n(A)*n(B)2. Правило произведения На столе лежат 5
13. n(AυB)=n(A)+n(B)-n(A B)3. Формула включений и исключений υ
14. РешениеА-мн.дождл. Дней n(A)=12В-мн.
15. A =nПравило размещения m n m
16. ЗадачаНа вокзальных путях стоит 6 светофоров, имеющих
17. Размещение без повторенияА =m n n m
18. Правило перестановки Р = !n n
19. Сочетание без повторения
20. РешениеС 2 30 = 30!2!(30-2)!=30*29*28*27…*22(28*27*…*2)= = 435Ответ:435
21. Сочетание с повторениемС m n = С
22. ВыводИтак, мы научились решать комбинаторные задачи. Но
23. Скачать презентацию
24. Похожие презентации

Цели и задачиЗнакомство с новым разделом математикиРассмотреть все тонкости этого разделаНаучиться решать задачи по комбинаторике

Цели и задачиЗнакомство с новым разделом математикиРассмотреть все тонкости этого разделаНаучиться решать задачи по комбинаторике

Комбинаторика очень нужный и сложный раздел математики. Он учит рассуждать, перебирая различные

КОМБИНАТОРИКА – область математики, в которой изучаются вопросы о том, сколько различных

ГРАФ – совокупность объектов со связями между ними. Объекты представляются как вершины,

ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ – граф, схема, отражающая структуру задачи, упорядочения многошагового процесса

КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления перебора всех возможных вариантов или

Из чисел 1, 5, 9 составить трёхзначное число без повторяющихся цифрРешение: (воспользуемся

Пример 2 Сколько двузначных чисел можно составить, используя цифры 1,4,7Решение: сначала запишем

1 Правило суммы:n(AυB)=n(A)+n(B), n-мощность множествn(A) - число элементов во множестве Пример: На

n(A*B)=n(A)*n(B)2. Правило произведения На столе лежат 5 груш, 7 яблок и 6

n(AυB)=n(A)+n(B)-n(A B)3. Формула включений и исключений υ В сентябре было 12 дождливых

РешениеА-мн.дождл. Дней n(A)=12В-мн. Ветреных

A =nПравило размещения m n m Где:«-»-элемент повторенияm-количество используемых элементовn- из

ЗадачаНа вокзальных путях стоит 6 светофоров, имеющих три разных цвета. Сколькими способами

Размещение без повторенияА =m n n m n ! ( )

Правило перестановки Р = !n n Сколько всего четырёхзначных чисел( в

РешениеС 2 30 = 30!2!(30-2)!=30*29*28*27…*22(28*27*…*2)= = 435Ответ:435

Сочетание с повторениемС m n = С n n +m-1 В магазине

ВыводИтак, мы научились решать комбинаторные задачи. Но то, что мы посмотрели, это

ЛитератураСвободная энциклопедия ВикипедияЖурнал «Математика в школе»

Слайды презентации

Слайд 2

Слайд 3 Цели и задачи
Знакомство с новым разделом математики
Рассмотреть все

тонкости этого раздела
Научиться решать задачи по комбинаторике

Слайд 4 Комбинаторика очень нужный и сложный раздел математики. Он

Комбинаторика очень нужный и сложный раздел математики. Он учит рассуждать, перебирая

учит рассуждать, перебирая различные варианты решения задачи, учит мыслить

нестандартно. Плюс к тому в заданиях ЕГЭ 2012 по математике будут задачи на комбинирование. Т.е. для хорошей сдачи экзаменов мы кроме всего остального должны знать и комбинаторику. К тому же, в жизни встречается масса задач связанных с комбинаторикой(мы их рассмотрим чуть позже)

Актуальность

Слайд 5 КОМБИНАТОРИКА – область математики, в которой изучаются вопросы

КОМБИНАТОРИКА – область математики, в которой изучаются вопросы о том, сколько

о том, сколько различных комбинаций, подчиненных тем или иным

условиям, можно составить из заданных объектов.

Слайд 6 ГРАФ – совокупность объектов со связями между ними.

ГРАФ – совокупность объектов со связями между ними. Объекты представляются как

Объекты представляются как вершины, или узлы графа, а связи

– как дуги, или ребра. Исследование графов ведется комбинаторными методами математики.

Слайд 7 ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ – граф, схема, отражающая структуру

ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ – граф, схема, отражающая структуру задачи, упорядочения многошагового

задачи, упорядочения многошагового процесса принятия решений. Ветви дерева отображают

различные события, которые могут иметь место, а корень дерева – состояние, в котором возникает необходимость выбора.

Слайд 8 КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления перебора

КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления перебора всех возможных вариантов

всех возможных вариантов или подсчета их числа.

ОРГАНИЗОВАННЫЙ ПЕРЕБОР –

строгий порядок разбора всех случаев, возможных решений.

Слайд 9 Из чисел 1, 5, 9 составить трёхзначное число

Из чисел 1, 5, 9 составить трёхзначное число без повторяющихся цифрРешение:

без повторяющихся цифр
Решение: (воспользуемся деревом возможных вариантов)

Решение элементарных задач

Дерево возможных вариантов

159

195

519

591

915

951

Ответ: 6 комбинаций

Слайд 10 Пример 2
Сколько двузначных чисел можно составить, используя

Пример 2 Сколько двузначных чисел можно составить, используя цифры 1,4,7Решение: сначала

цифры 1,4,7
Решение: сначала запишем числа начинающиеся с цифры 1,затем

4 и 7
11 14 17
41 44 47
71 74 77

Ответ:9

Слайд 11 1 Правило суммы:
n(AυB)=n(A)+n(B), n-мощность множеств
n(A) - число элементов

1 Правило суммы:n(AυB)=n(A)+n(B), n-мощность множествn(A) - число элементов во множестве Пример:

во множестве
Пример: На одной полке книжного шкафа стоит

45 различных книг, а на другой – 55 различных книг (и не таких, как на первой полке), сколькими способами можно выбрать одну книгу из стоящих на этих полках? Решение:
n(A)=45(книги первой полки)
n(B)=55(книги второй полки)
n(AυB)=n(A)+n(B)=45+55=100

9 Правил комбинаторики

Ответ:100 вариантов

Слайд 12 n(AB)=n(A)n(B)
2. Правило произведения
На столе лежат 5 груш,

n(A*B)=n(A)*n(B)2. Правило произведения На столе лежат 5 груш, 7 яблок и

7 яблок и 6 мандаринов. Сколькими способами ребёнок может

выбрать для себя набор из этих фруктов(притом размеры каждого фрукта различны)
A-множество груш
В-множество яблок
С-множество мандаринов
N(A*B*C)=n(A)*n(B)*n(C)=5*7*6=210

Овет:210 вариантов

Слайд 13 n(AυB)=n(A)+n(B)-n(A B)

3. Формула включений и исключений
υ

n(AυB)=n(A)+n(B)-n(A B)3. Формула включений и исключений υ В сентябре было 12

В сентябре было 12 дождливых дней, 8 ветряных,10 холодных,

6 и дождливых, и ветреных; 7 и дождливых, и холодных; 5 и ветреных, и холодных; з дня и дождливых, и ветреных и холодных. Сколько дней в сентябре была хорошая погода?

Слайд 14 Решение
А-мн.дождл. Дней n(A)=12
В-мн. Ветреных

n(B)=8
С-мн. Холодных

n(C)=10
D-мн.хороших дней

n(AB)=6, n(AC)=7, n(BC)=5, n(ABC)=3
n(AυBυC)=n(A)+n(B)+n(C)-n(AB)-n(AC)-n(BC)+n(ABC)=12+8+10-6-7-5+3=15

D=30-15=15

Ответ:15 дней

Слайд 15 A =n
Правило размещения
m
n
m
Где:
«-»-элемент

повторения
m-количество используемых элементов
n- из скольких элементов состоит
Если порядок важен

используется А, если нет, то С(познакомимся чуть позже)

Слайд 16 Задача
На вокзальных путях стоит 6 светофоров, имеющих три

ЗадачаНа вокзальных путях стоит 6 светофоров, имеющих три разных цвета. Сколькими

разных цвета. Сколькими способами можно дать различные сигналы на

этих путях
Решение:
В данном случае важен порядок и есть повторение, то

А =3=729

Ответ:729

Слайд 17 Размещение без повторения
А =
m
n
n
m
n

!
( )
!
Абонент набирая номер знакомого

по телефону забыл последние 2 цифры и помня лишь, что они различны, набрал его наугад. Сколько возможных вариантов существует для абонента набрать верный номер

А =

10!
(10-8)!

10*9*8*….*1

8*7*6*5*4*3*2*1

Ответ:90

Слайд 18 Правило перестановки
Р = !
n
n
Сколько

всего четырёхзначных чисел( в которых цифры не повторяются) можно

написать используя числа 2,3,4,9

Р =4!=4*3*2=24

Ответ: 24

Слайд 19 Сочетание без повторения

Ежедневно из 30-ти учеников для дежурства выделяются 2 ученика по списку. Можно ли составить график на весь учебный год, чтобы никакие 2 ученика не дежурили вместе дважды в течение учебного года(уч. год 210 дн)