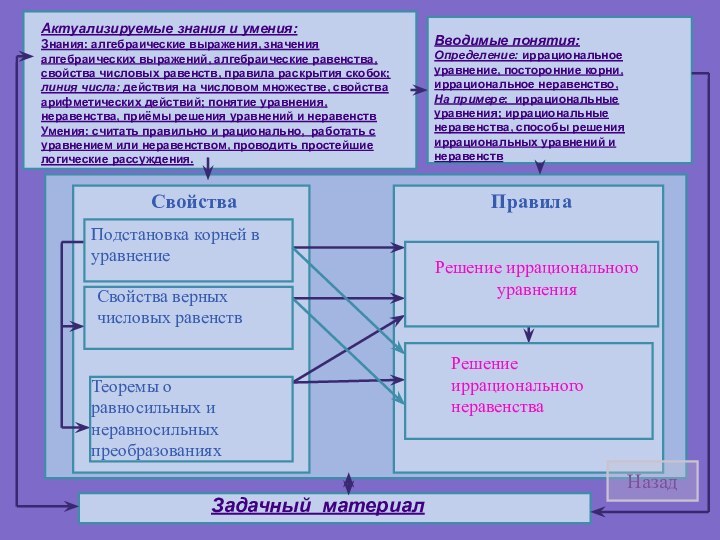
работы с понятием
Пример работы с теоремой
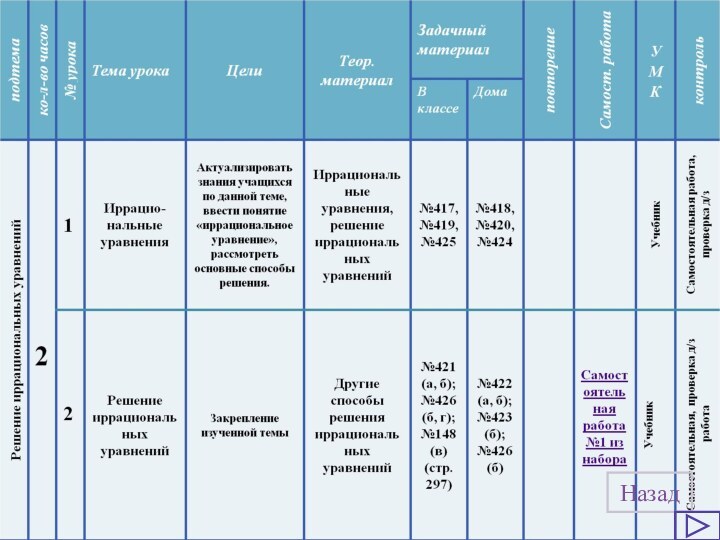
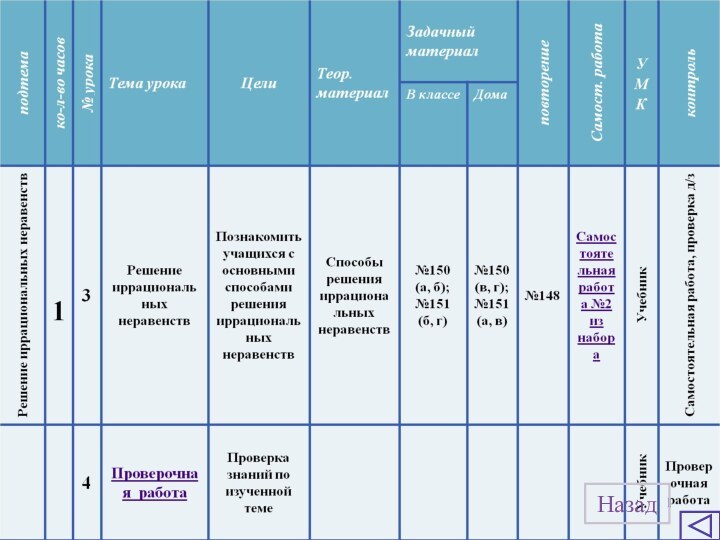
Пример работы с задачей
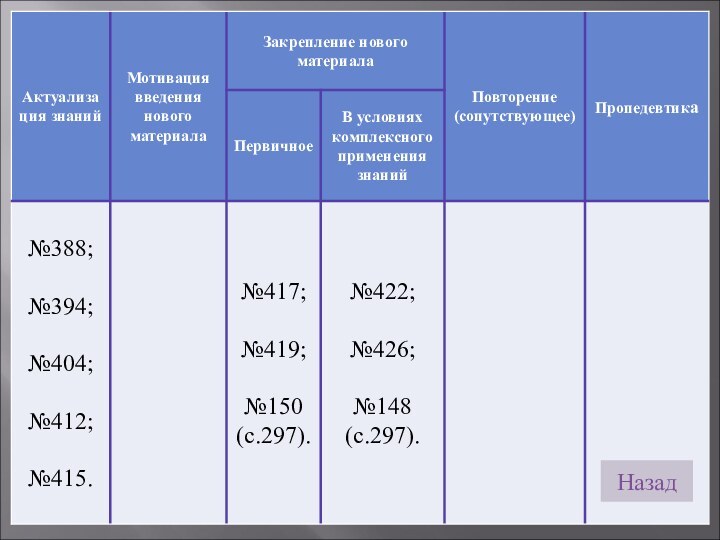
Дополнительные
задачи Система контроля
Использованная литература
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






























Назад
Назад
Назад
Назад
Назад
Назад
Назад