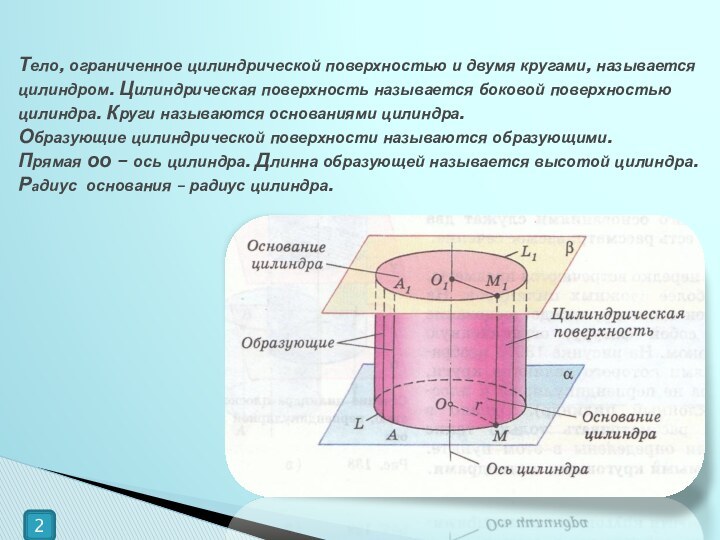
Цилиндрическая поверхность называется боковой поверхностью цилиндра. Круги называются основаниями
цилиндра. Образующие цилиндрической поверхности называются образующими. Прямая оо – ось цилиндра. Длинна образующей называется высотой цилиндра. Радиус основания – радиус цилиндра.2