Презентация на тему по геометрии на тему: Замечательные точки

угла

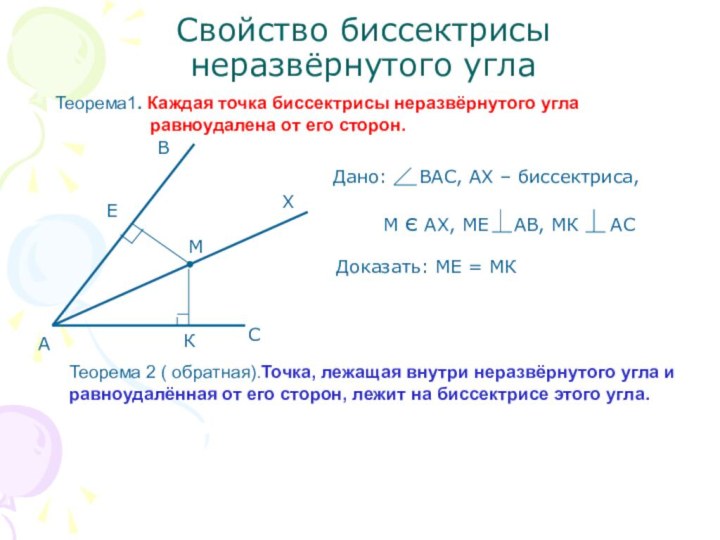
Доказать: МЕ = МК

Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.

перпендикуляра к отрезку

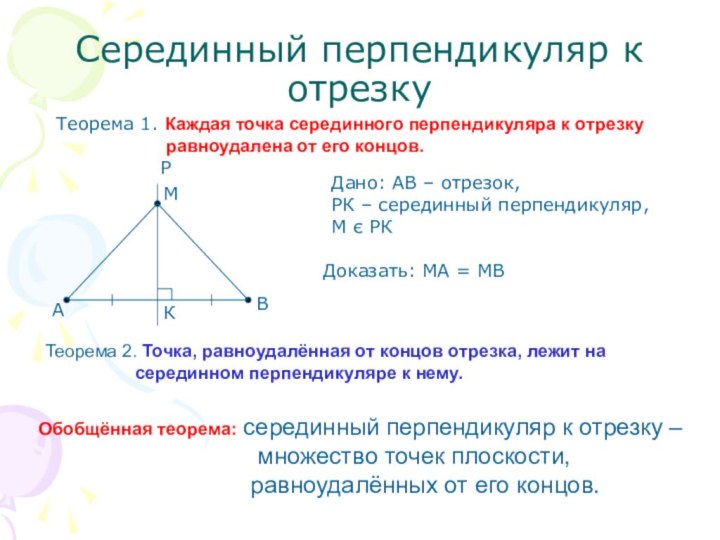
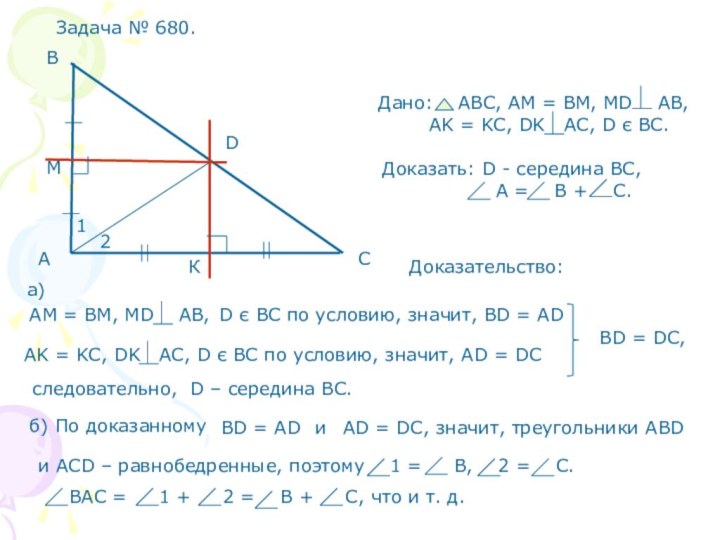
Дано: АВ – отрезок,
РК – серединный перпендикуляр,
М є РК

Доказать: МА = МВ

Теорема 2. Точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к нему.

Обобщённая теорема: серединный перпендикуляр к отрезку –
множество точек плоскости,
равноудалённых от его концов.

одной точке.
Доказательство:
Значит, О – точка пересечения трёх биссектрис треугольника.

треугольника
пересекаются

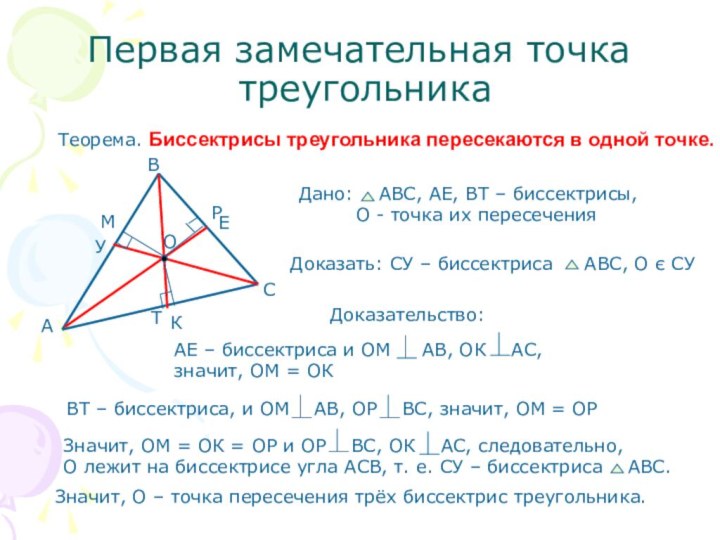
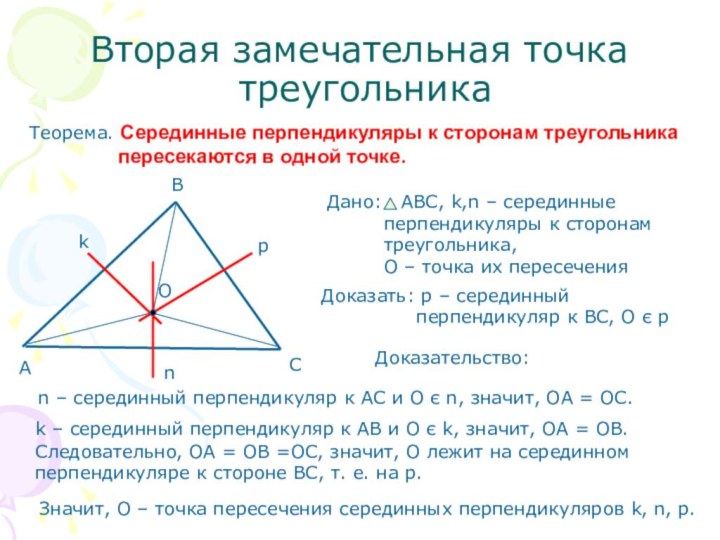
Доказать: р – серединный
перпендикуляр к ВС, О є р

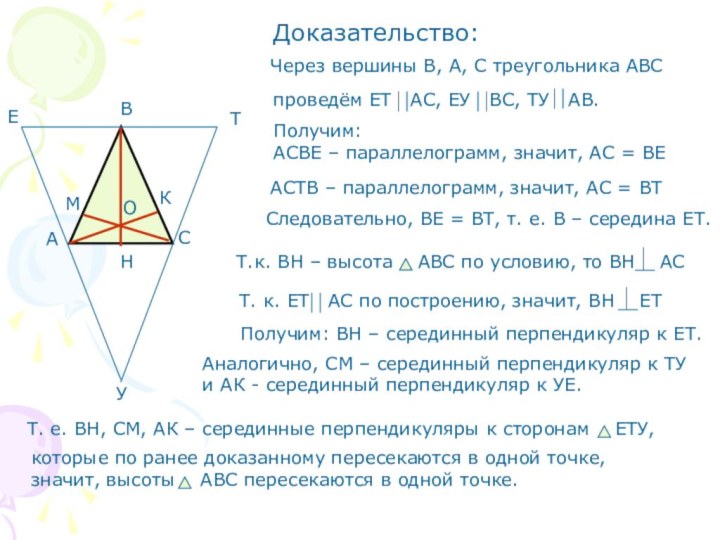
Доказательство:

n – серединный перпендикуляр к АС и О є n, значит, ОА = ОС.

k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ.

Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном
перпендикуляре к стороне ВС, т. е. на р.

Значит, О – точка пересечения серединных перпендикуляров k, n, p.

одной точке,

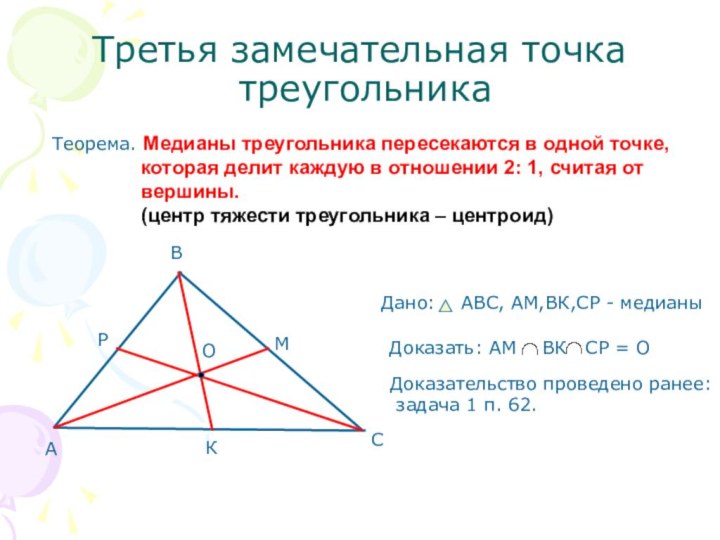
Доказательство проведено ранее:
задача 1 п. 62.

продолжения

– параллелограмм, значит, АС = ВТ
Следовательно, ВЕ = ВТ,

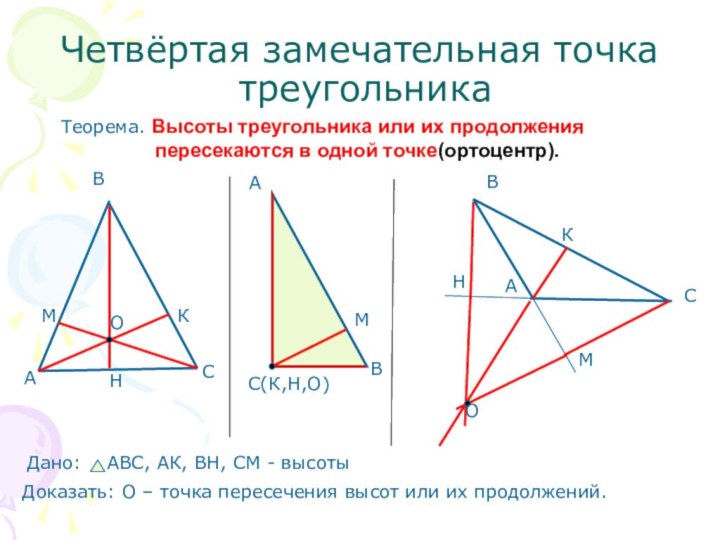
Получим: ВН – серединный перпендикуляр к ЕТ.

Аналогично, СМ – серединный перпендикуляр к ТУ
и АК - серединный перпендикуляр к УЕ.