Презентация на тему Теорема Пифагора

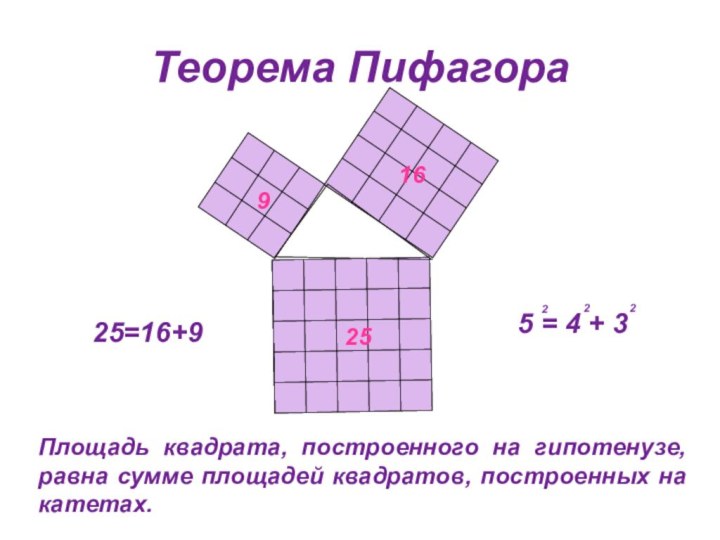
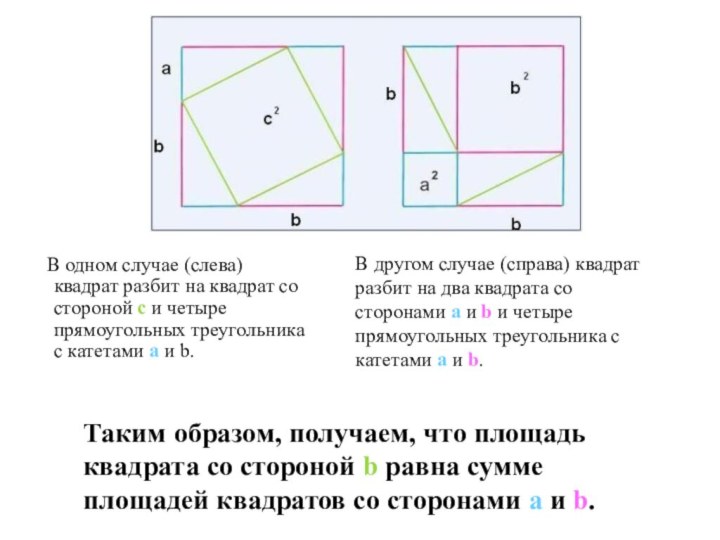
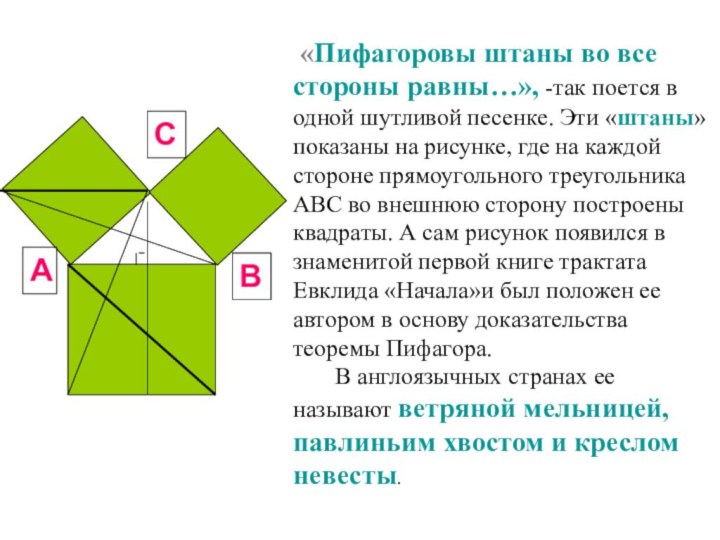
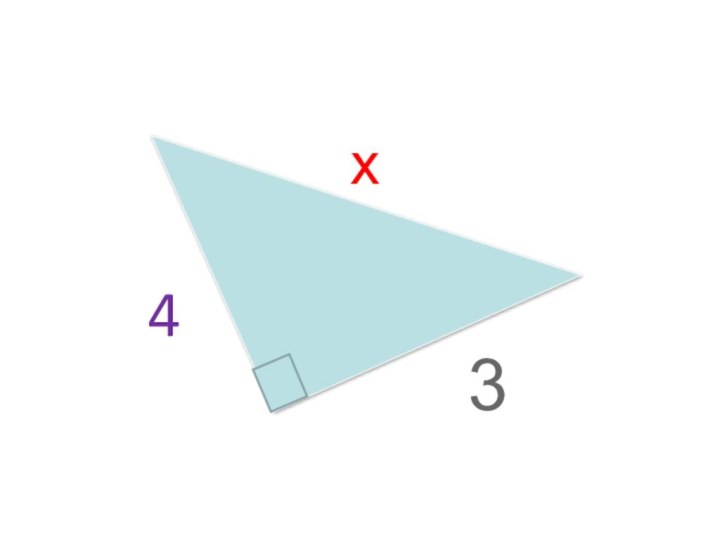
Родился: около 569 г. до н.э. на острове Самос

в Ионическом море. Умер: около 475 г. до РХ.
Пифагор был:
  1. известным кулачным бойцом Олимпийских игр.   2. ведущим духовным, церковным и научным идеологом своего государства.
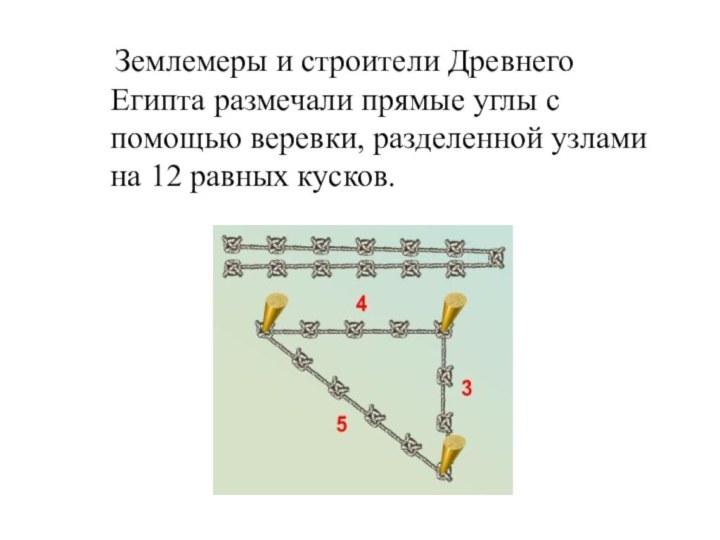
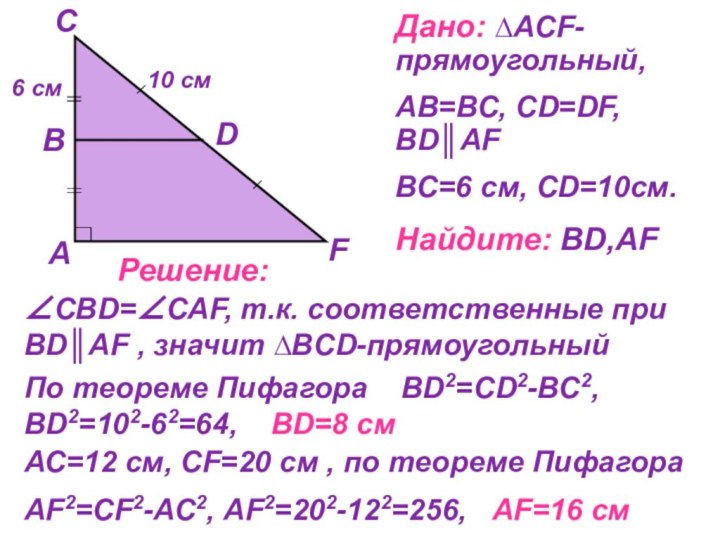
В молодости для изучения наук жрецов путешествовал по Египту, жил также в Вавилоне, где имел возможность в течение 12 лет изучать астрологию и астрономию у халдейских Жрецов. После Вавилона, побыв некоторое время в своём отечестве, переселился в Южную Италию, потом в Сицилию и организовал там пифагорейскую школу, которая внесла ценный вклад в развитие математики и астрономии.

квадратов, построенных на катетах».
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме

квадратов катетов».

Во времена Пифагора формулировка теоремы звучала так:

Современная формулировка
теоремы Пифагора

площадей квадратов, построенных на катетах.

равна a + b.
b
a

на квадрат со стороной с и четыре прямоугольных треугольника

с катетами a и b.

a

b

a

b

В другом случае (справа) квадрат разбит на два квадрата со сторонами a и b и четыре прямоугольных треугольника с катетами a и b.

a

b

Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и b.

поется в одной шутливой песенке. Эти «штаны» показаны на

рисунке, где на каждой стороне прямоугольного треугольника АВС во внешнюю сторону построены квадраты. А сам рисунок появился в знаменитой первой книге трактата Евклида «Начала»и был положен ее автором в основу доказательства теоремы Пифагора.
В англоязычных странах ее называют ветряной мельницей, павлиньим хвостом и креслом невесты.

квадратов двух других сторон, то треугольник прямоугольный
Обратная теореме

Пифагора

обладают рядом интересных особенностей, которые мы перечислим без доказательств:

Один из «катетов» должен быть кратным трём.
Один из «катетов» должен быть кратным четырём.
Одно из пифагоровых чисел должно быть кратно пяти.

размечали прямые углы с помощью веревки, разделенной узлами на

12 равных кусков.

Посмотри!

любыми другими правильными многоугольниками или полукругами.

по одну сторону гипотенузы, то площадь полученных луночек равна

площади данного треугольника.

иррациональное число. Улитка Архимеда.

«Смотри чертёж».
Догадайтесь сами, как построены отрезки с такими длинами.

можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом

а. Таким образом:
d2=2a², d= a.

вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с

катетами a и b. Мы имеем d²=a²+b² .
d=

d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке.

Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а). Отсюда имеем d2 = a2+( а)2, d2=3a2, d= a.

параллелепипеда с ребрами a, b, с и получить для

диагонали выражение
d =

Пифагория и напоминает всем о теореме Пифагора, наиболее известном

его открытии. Катет, лежащий в основании треугольника - мраморный , гипотенуза и фигура самого Пифагора в виде второго катета - медные.

МN2