Презентация на тему геометрические задачи

Содержание

2. Цель исследования: активизация поисково-познавательной деятельности
3. Задачи:Воспитание исследовательских умений и навыковНаучиться приблизить учебные задачи к жизненно практическим ситуациям
4. На уроках
5. Имея модель, можно ответить на вопросы:Вид полученных
6. Гипотеза: Если увеличить количество палочек,
7. Исследование:Выложив 7 палочек, видим,что получены модели 3 правильных треугольников, 2 ромбов,1трапеции. Наибольшим является трапеция.
8. Выложив 8 палочек, получил один квадрат, два треугольника и шестиугольник
9. Из 9 палочек составили 4 треугольника,3 ромба,
10. Практическое применение моделей:
11. Наибольшим из трёх четырёхугольников является трапеция.а) угол
12. Литература:Калинина О.Ф. Занятия по новой педагогической
13. Скачать презентацию
14. Похожие презентации

Цель исследования: активизация поисково-познавательной деятельности

Некоторые геометрические задачи конструктивного характераВыполнил ученик 7 «к» классаПетров ВадимМОУ «Трёхбалтаевская СОШ»

Задачи:Воспитание исследовательских умений и навыковНаучиться приблизить учебные задачи к жизненно практическим ситуациям

Имея модель, можно ответить на вопросы:Вид полученных фигурОпределить углы четырёхугольникаВычислить диагонали, высоту,

Гипотеза: Если увеличить количество палочек, например, взять семь, восемь, девять

Исследование:Выложив 7 палочек, видим,что получены модели 3 правильных треугольников, 2 ромбов,1трапеции. Наибольшим является трапеция.

Выложив 8 палочек, получил один квадрат, два треугольника и шестиугольник

Из 9 палочек составили 4 треугольника,3 ромба, 2 трапеции и параллелограмм, не

Наибольшим из трёх четырёхугольников является трапеция.а) угол ВАЕ = угол АЕД =

Литература:Калинина О.Ф. Занятия по новой педагогической технологии.Клименченко Д.В. Некоторые геометрические

Заключение Геометрические задачи конструктивного характера позволяют активизировать поисково – познавательную

Слайды презентации

Слайд 2 Цель исследования:
активизация поисково-познавательной деятельности

Слайд 3 Задачи:
Воспитание исследовательских умений и навыков
Научиться приблизить учебные задачи

к жизненно практическим ситуациям

Слайд 4
На уроках геометрии

На уроках геометрии мы решаем задачи, в условиях

мы решаем задачи, в условиях которых явно указывается вид

геометрической фигуры, задаются некоторые её элементы или отношения и ставится вопрос найти неизвестные элементы.
Есть также задачи на моделирование. Например, в качестве моделей отрезков можно использовать палочки и задача превращается в модель некоторой реальной ситуации. Так, задача: из пяти одинаковых палочек, не накладывая одну на другую, составить 2 треугольника и четырёхугольник, заинтересовала меня. Построил модель:

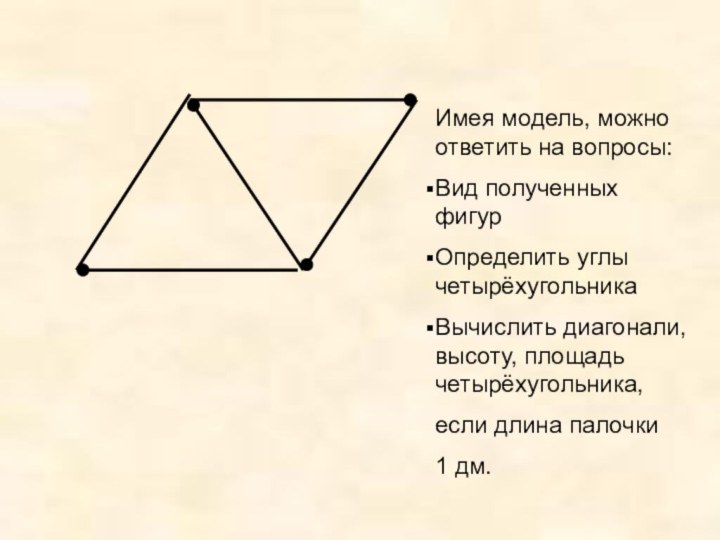
Слайд 5 Имея модель, можно ответить на вопросы:
Вид полученных фигур
Определить

Имея модель, можно ответить на вопросы:Вид полученных фигурОпределить углы четырёхугольникаВычислить диагонали,

углы четырёхугольника
Вычислить диагонали, высоту, площадь четырёхугольника,
если длина палочки
1

дм.

Слайд 6 Гипотеза:
Если увеличить количество палочек, например,

взять семь, восемь, девять одинаковых палочек, то сколько треугольников

и сколько четырёхугольников можно получить и каковы их
характеристические свойства.

Слайд 7 Исследование:

Выложив 7 палочек, видим,что получены модели 3 правильных

треугольников, 2 ромбов,1трапеции. Наибольшим является трапеция.

Слайд 8 Выложив 8 палочек, получил один квадрат, два треугольника

и шестиугольник

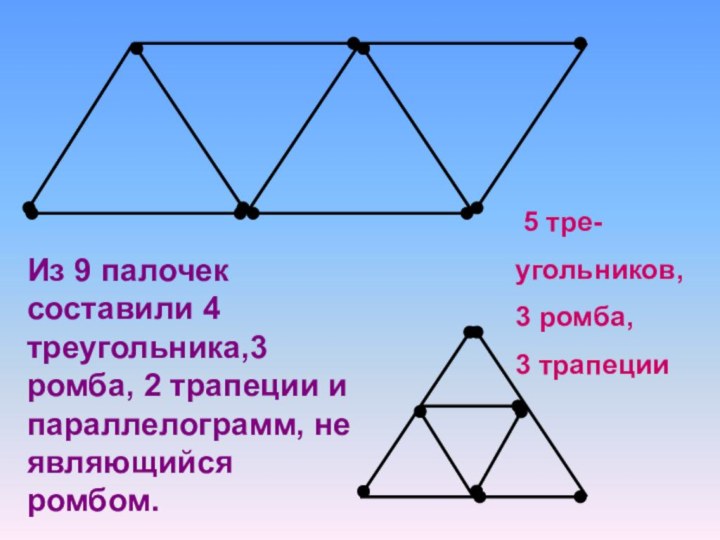
Слайд 9 Из 9 палочек составили 4 треугольника,3 ромба, 2

Из 9 палочек составили 4 треугольника,3 ромба, 2 трапеции и параллелограмм,

трапеции и параллелограмм, не являющийся ромбом.

5 тре-
угольников,
3

ромба,
3 трапеции

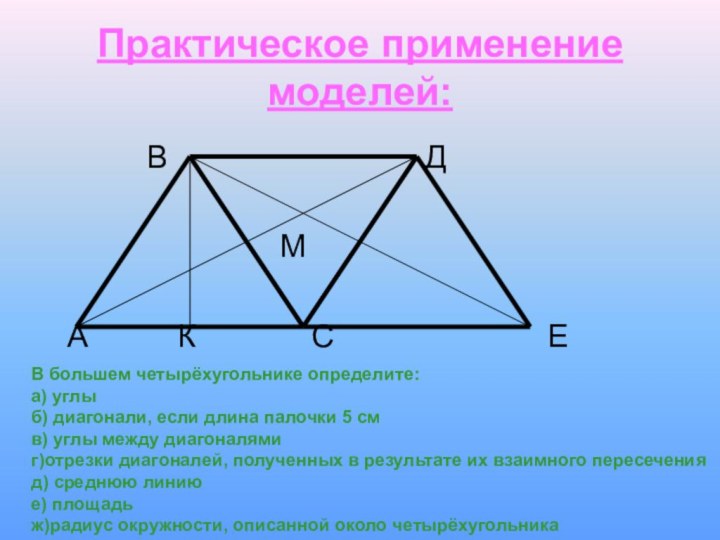
Слайд 10 Практическое применение моделей:

В

Д

М

А К С Е

В большем четырёхугольнике определите:
а) углы
б) диагонали, если длина палочки 5 см
в) углы между диагоналями
г)отрезки диагоналей, полученных в результате их взаимного пересечения
д) среднюю линию
е) площадь
ж)радиус окружности, описанной около четырёхугольника

Слайд 11 Наибольшим из трёх четырёхугольников является трапеция.

а) угол ВАЕ

= угол АЕД = 60° ; угол АВД =

угол ВДЕ = 120° ;

б) АД = ВЕ, так как трапеция равнобочная; ВЕ = √( АЕ ² - АВ ² ) ,так как
угол АВЕ = 60° + 30° = 90° ; ВЕ = √ (( 5*2)² - 5² ) = 5√3 (см).

в) угол АЕМ = угол МАЕ = 30°; угол АМЕ = 180° - (30° + 30° ) = 120°;
угол АМВ = 180° - 120° = 60°ْ;

г) ΔАМЕ подобен ΔВМД, поэтому АЕ/ВД = МЕ/ ВМ = 2;
ВМ =ДМ = ВЕ:3 = 5√3 /3 (см); АМ = ЕМ = 5√3: 3*2 = 10√3/ 3(см).
д) средняя линия трапеции равна (5 + 10)/2 = 7,5(см);

е)SАВДЕ = 7,5* ВК; ВК = 5√3 /2 * 15/2 = 75√3 /4 (см²).

ж) Так как угол АВЕ = 90°, то АЕ - диаметр описанной окружности,
значит, R = 1/ 2 АЕ = 5 (см).