Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии на тему Второй признак равенства треугольников (7класс)

Содержание

Проверка домашнего задания
Домашняя работа:п. 19 с. 37 – 38 учить,с. 40 № 122, с.36 № 111. Проверка домашнего задания Если в треугольнике медиана совпадает с высотой, то этот треугольник равнобедренный.Дано: АВСAD Теорема: В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.Дано: ВСТНазовите углы, прилежащие к стороне ВТ.Назовите углы, прилежащие к стороне СТ. ВСТНазовите углы, прилежащие к стороне ВС. Второй признак равенства треугольников Теорема Если сторона и два прилежащих к ней угла одного треугольника соответственно Сформулируйте второй признак равенства треугольников.Какие элементы треугольников равны во втором признаке равенства треугольников? АCDOДоказать:АOD = BOCВ12 1 = 2Дано:a) Доказать:CАВ = ACDб) найти СD и BC,если AD = Дано:Доказать:TXE = TSETE – биссектриса  XTS34121 = 2 № 123 На биссектрисе угла А взята точка D, а на сторонах Сформулируйте второй признак равенства треугольников.Какие элементы треугольников равны во втором признаке равенства треугольников?
Слайды презентации

Слайд 2 Проверка домашнего задания

Проверка домашнего задания

Слайд 3 Если в треугольнике медиана совпадает с высотой, то

Если в треугольнике медиана совпадает с высотой, то этот треугольник равнобедренный.Дано:

этот треугольник равнобедренный.
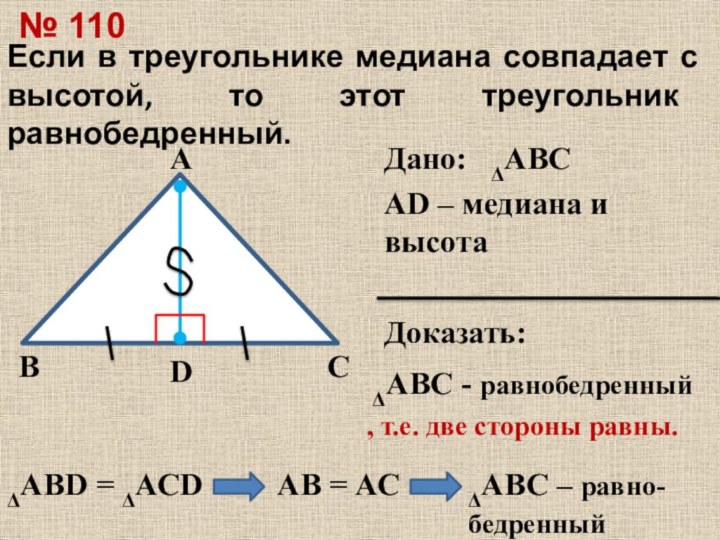
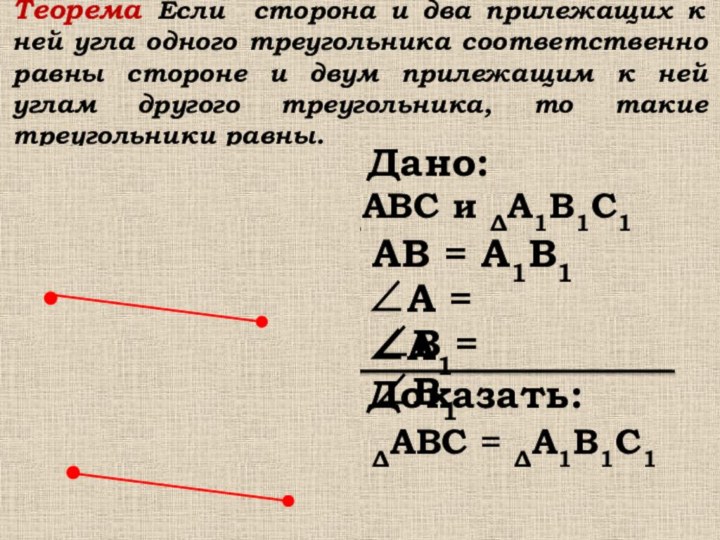
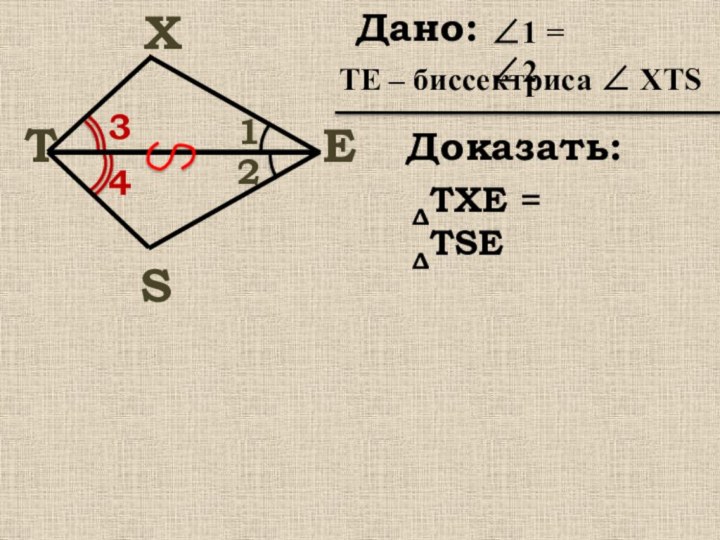
Дано:
АВС
AD – медиана и высота
Доказать:
А
В
С
D
АВD

= АСD

АВ = АС

АВС - равнобедренный

АВС – равно-
бедренный

, т.е. две стороны равны.

№ 110

Слайд 4 Теорема:
В равнобедренном треугольнике биссектриса, проведённая к основанию,

Теорема: В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и

является медианой и высотой.
Дано:
АВС - равнобедренный
ВС -

основание

Доказать:

А

В

С

D

АВD = АСD

1

2

 3 = 4

АD - биссектриса

1) АD - медиана

2) АD - высота

ВD = СD

, то D – середина АС

3

4

, но они смежные, то

 3 =4= 180º:2=90º

Слайд 5 В
С
Т
Назовите углы, прилежащие к стороне ВТ.
Назовите углы, прилежащие

ВСТНазовите углы, прилежащие к стороне ВТ.Назовите углы, прилежащие к стороне СТ.

к стороне СТ.

Слайд 6 В
С
Т
Назовите углы, прилежащие к стороне ВС.

ВСТНазовите углы, прилежащие к стороне ВС.

Слайд 7 Второй признак равенства треугольников

Второй признак равенства треугольников

Слайд 8 Теорема Если сторона и два прилежащих к ней

Теорема Если сторона и два прилежащих к ней угла одного треугольника

угла одного треугольника соответственно равны стороне и двум прилежащим

к ней углам другого треугольника, то такие треугольники равны.

А

C

B

А1

C1

B1

АB = А1B1

А = А1

АВС и А1В1С1

Дано:

Доказать:

АВС = А1В1С1

В = В1

Слайд 9 Сформулируйте второй признак равенства треугольников.
Какие элементы треугольников равны

Сформулируйте второй признак равенства треугольников.Какие элементы треугольников равны во втором признаке равенства треугольников?

во втором признаке равенства треугольников?

Слайд 10 А
C
D
O
Доказать:
АOD = BOC
В
1
2

АCDOДоказать:АOD = BOCВ12

Слайд 11 1 = 2
Дано:
a) Доказать:
CАВ = ACD
б) найти СD

1 = 2Дано:a) Доказать:CАВ = ACDб) найти СD и BC,если AD

и BC,
если AD = 17см,
АВ = 15 см.
3

= 4

А

В

C

D

1

2

3

4

17

15

Слайд 12 Дано:
Доказать:
TXE = TSE
TE – биссектриса  XTS
3
4
1
2
1 =

Дано:Доказать:TXE = TSETE – биссектриса  XTS34121 = 2

2

Слайд 13 № 123
На биссектрисе угла А взята точка

№ 123 На биссектрисе угла А взята точка D, а на

D, а на сторонах этого угла – точки В

и С такие, что ADB = ADC. Докажите, что BD = CD.

А

D

B

C

Дано:

A,

AD - биссектриса

точки В и С сторонам А

ADB = ADC

Доказать: BD = CD

  • Имя файла: prezentatsiya-po-geometrii-na-temu-vtoroy-priznak-ravenstva-treugolnikov-7klass.pptx
  • Количество просмотров: 145
  • Количество скачиваний: 0
- Предыдущая Презентация к уроку на тему Инфракрасные лучи
Следующая - Презентация к уроку Противоречивость прогресса

Похожие презентации

Подобные треугольники. Признаки подобия треугольников Подобные треугольники. Признаки подобия треугольников 162
Презнтация к уроку геометрии в 7 классе Равнобедренный треугольник и его свойства. Презнтация к уроку геометрии в 7 классе Равнобедренный треугольник и его свойства. 164
Признаки паралельности прямых Признаки паралельности прямых 150
Презентация по геометрии на тему Тригонометрические функции Презентация по геометрии на тему Тригонометрические функции 163
Многоугольники и их виды Многоугольники и их виды 198
Танграм Танграм 156
Айналу денелер тақырыбына геометриядан презентация Айналу денелер тақырыбына геометриядан презентация 240
Презентация по геометрии 9 класс Векторы Презентация по геометрии 9 класс Векторы 200
Треугольники Треугольники 154
Многоугольники 8 класс Многоугольники 8 класс 167
Зарождение геометрии Зарождение геометрии 162
Построение общих касательных к двум окружностям на плоскости Построение общих касательных к двум окружностям на плоскости 143
Решение задач на вписанные углы Решение задач на вписанные углы 164
Презентация по геометрии Правильная пирамида(10 класс) Презентация по геометрии Правильная пирамида(10 класс) 156
Новая геометрия Николая Лобачевского Новая геометрия Николая Лобачевского 146
Определение подобных треугольников Определение подобных треугольников 181
Решение заданий С2 ЕГЭ-2010 Решение заданий С2 ЕГЭ-2010 163
Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости) Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости) 171
Презентация по математике к уроку по темеМногогранники Презентация по математике к уроку по темеМногогранники 138
Десять решений одной задачи Десять решений одной задачи 165
Решение прямоугольных треугольников Решение прямоугольных треугольников 227
Перпендикуляр и наклонная Перпендикуляр и наклонная 169
Презентация по геометрии Усеченная пирамида (10 класс) Презентация по геометрии Усеченная пирамида (10 класс) 210
Презентация к уроку 4 замечательные точки Презентация к уроку 4 замечательные точки 148
Путешествие в мир геометрии Путешествие в мир геометрии 177
Тест по теме Усеченная пирамида Тест по теме Усеченная пирамида 304
Подібність прямокутних трикутників Подібність прямокутних трикутників 166
Объем цилиндра Объем цилиндра 132
Вводное повторение Вводное повторение 160
Окружность геометрия Окружность геометрия 203