Слайд 2
Цели урока
Образовательные:
- вывести формулы синуса, косинуса и тангенса
двойного угла ;
- формировать умения применять формулы синуса, косинуса
и тангенса двойного угла при решении задач;
- закрепить навыки использования тригонометрических формул при решении задач;
- сформировать у учащихся прочные практические знания при применении тригонометрических формул.
Развивающие:
- развивать самостоятельную познавательную активность обучающихся, память, логическое мышление, умение применять знания в будущей профессии;
- развивать исследовательские умения: извлекать информацию из разных источников, работать с разными видами информации.
Воспитательные:
- создать условия для осознания необходимости самостоятельных действий при решении проблем;
- обучать объективной оценке своих возможностей и успехов;
- формировать умение оценивать свой уровень знаний и стремление его повышать;
- способствовать развитию потребности к самообразованию;
- воспитание ответственности, коллективизма.
Слайд 3
Мир тригонометрии
Тригонометрия делится на плоскую
( прямолинейную)
и сферическую тригонометрию
Теория тригонометрических функций (гониометрия) и её приложения
к решению плоских треугольников мы с вами изучаем в средней школе .
Исторически сферическая тригонометрия и геометрия возникли из потребностей астрономии, геодезии, навигации, картографии.
Слайд 4
Мир тригонометрии
Восход и
заход солнца, изменение фаз луны, чередование времен года, биение
сердца, циклы в жизнедеятельности организма, вращение колеса, морские приливы и отливы - модели этих многообразных процессов описываются тригонометрическими функциями.
Звук, электрический ток, радио представляют собой колебания различной частоты и амплитуды.
Если бы зрение людей обладало способностью видеть звуковые, электромагнитные и радиоволны, то мы видели бы вокруг многочисленные синусоиды всевозможных видов.
Слайд 5
Психологический тест
Однажды великого
греческого философа Сократа спросили о том, что, по его
мнению, легче всего в жизни. Он ответил, что легче всего поучать других, а труднее – познать самого себя.
Мы познаем окружающий нас мир. Но сегодня давайте заглянем в себя.
Как мы воспринимаем окружающий мир? Как художники или как мыслители?
Слайд 6
Психологический тест
1). Переплетите пальцы рук.
Большой палец какой руки оказался у Вас сверху?
Запишите результат буквами «Л» или «П».
2). Скрестите руки на груди (поза «Наполеона»). Кисть, какой руки оказалась сверху?
Запишите результат буквами «Л» или «П».
3). Изобразите «бурные аплодисменты».
Ладонь, какой руки у Вас сверху?
Запишите результат буквами «Л» или «П».
Слайд 7
Подведем итоги
Результат «ЛЛЛ» - Вы «художник»
У «художников»
- более развитое правое полушарие и преобладает образное мышление
Результат
«ППП» - Вы «мыслитель»
У «мыслителей» –более развитое правое левое полушарие и логическое мышление
Слайд 8
Упростить
cos 3α cos α + sin 3α
sinα
sin 2α cos α - cos 2α sin
α
Вычислить
а) cos 18 cos 12 – sin18 sin12
б)
г) sin α и tg α, если cos α =0,8
и 0 < α <
sin 2α, cos
2α и tg 2α,
если cos α =0,8
sin α =0,6 и tg α=3/4
и 0 < α <
Слайд 11
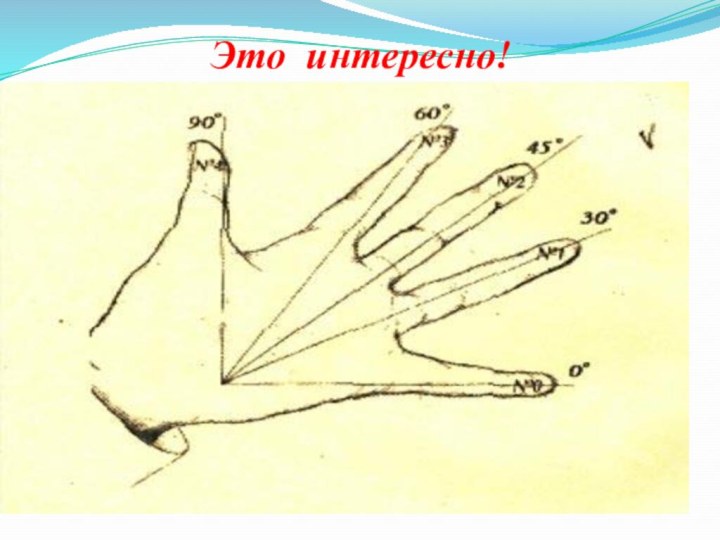
Это интересно!
Оказывается, значения синусов и
косинусов углов «находятся» на вашей ладони.
Протяните руку (любую)
и разведите как можно сильнее пальцы.
Оказывается между мизинцем и большим пальцем угол 90, между мизинцем и безымянным – 30, между мизинцем и средним – 45, между мизинцем и указательным – 60.
И это у всех людей без исключения.
Если пальцы считать лучами, исходящими из бугра Луны на ладони, то можно считать, что направление мизинца соответствует началу отсчета углов, т.е.
0 градусов.
Слайд 13
Это интересно!
Введем нумерацию
пальцев:
мизинец № 0 – соответствует 0,
безымянный № 1 – соответствует 30,
средний № 2 – соответствует 45,
указательный № 3 – соответствует 60,
большой № 4 – соответствует 90.
Слайд 14
Формулы двойного угла
Решение задач
Презентация выполнена учащимся 112 группы
КС
и ПТ Симановским Максимом
Санкт – Петербург
2016
Слайд 15
"Дорогу осилит идущий, а математику -мыслящий"
Слайд 16
Формулы двойного угла
Sin 2a = 2 sin a
cos a
Cos 2a = cos2 a – sin2 a
Cos
2a = 2cos2 a – 1
Cos 2a = 1 – 2sin2 a
tg 2a = ( 2 tg a) / (1 – tg2 a)
1 – cos 2a = 2 sin2 a
1 + cos 2a = 2 cos2 a
Слайд 18
Упростите выражение
Пример 1
Пример 2
Слайд 22
1.Упростите выражения:
2.Известно,что
Найдите:
Самостоятельная работа
I уровень(ЛЛЛ)
II уровень(ППП)
1. Упростите
выражения:
2. Известно, что
Найдите: