плечо имеет длину 2 м, а длинное плечо –
5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?3,5
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

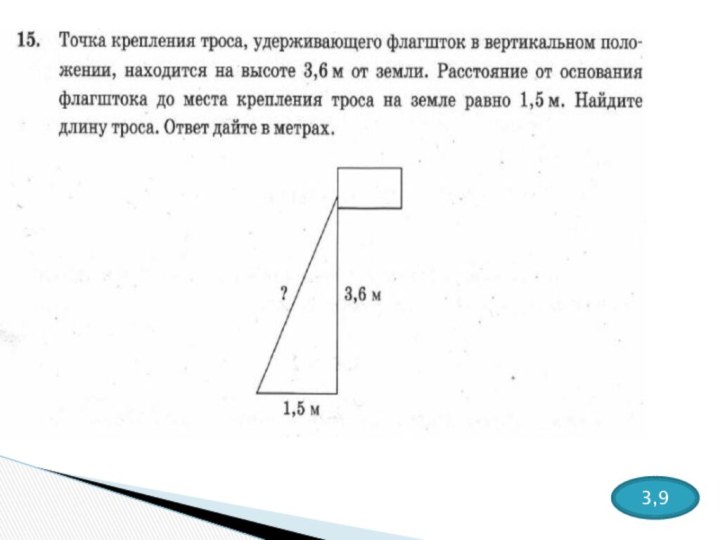




















3,5
16
142
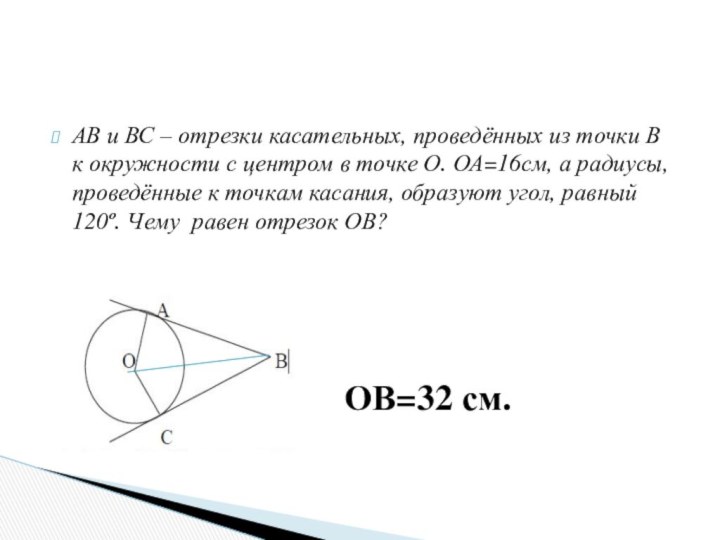
ОВ=32 см.
А
Треугольники ОАС и ОАВ- равные прямоугольные.
∟А=60º, тогда ∟ВАО=∟САО=60:2=30º,
. ОА=6см, тогда R=ОВ=ОС=6:2=3
Выбери верное утверждение
13
12
23
2
12