строить симметричные точки и уметь распознавать фигуры, являющиеся симметричными
относительно точки или прямой;Совершенствовать навыки решения задач;
Продолжить работу над аккуратностью записи и выполнения геометрического чертежа
Задачи урока:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





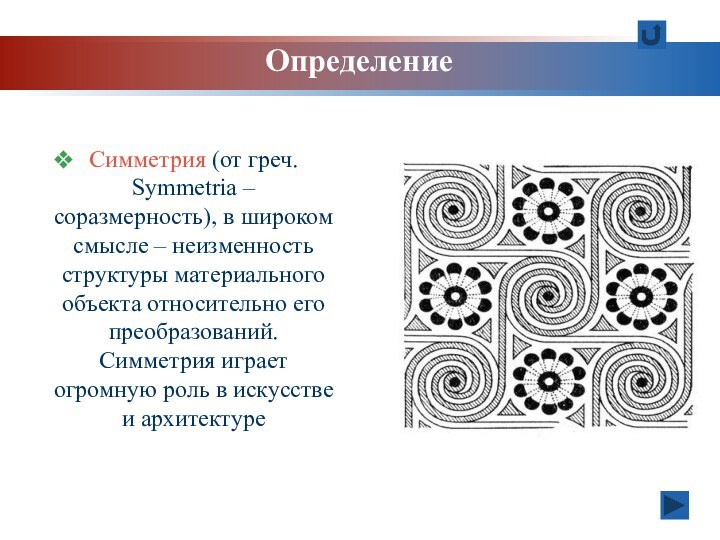


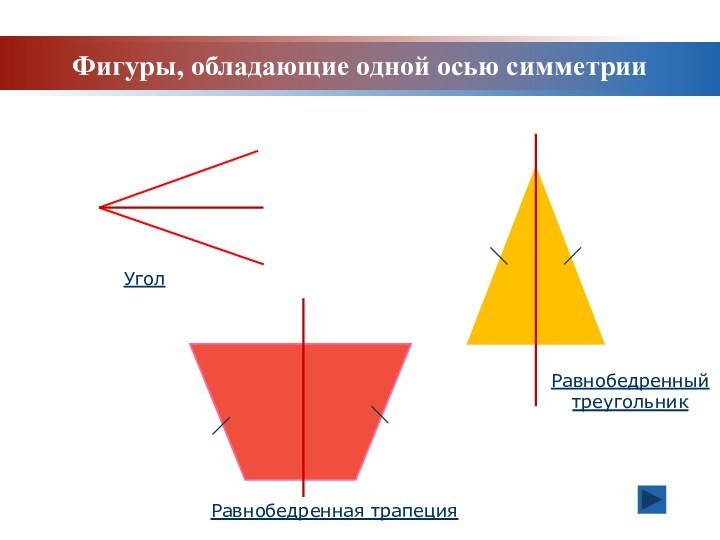
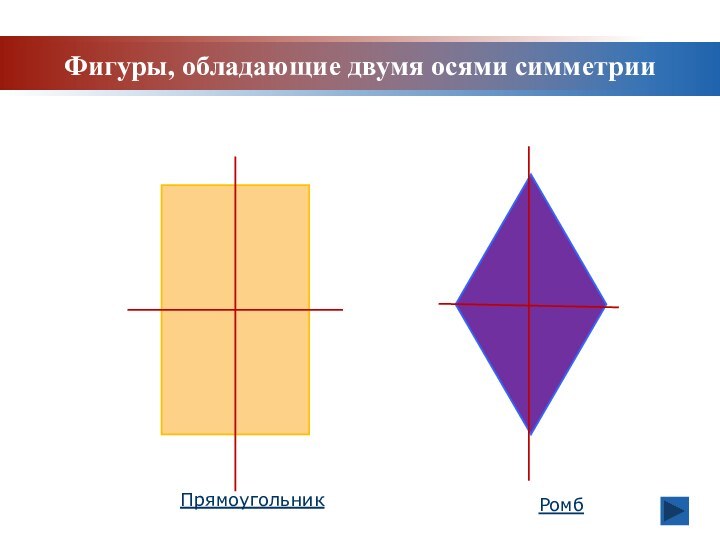
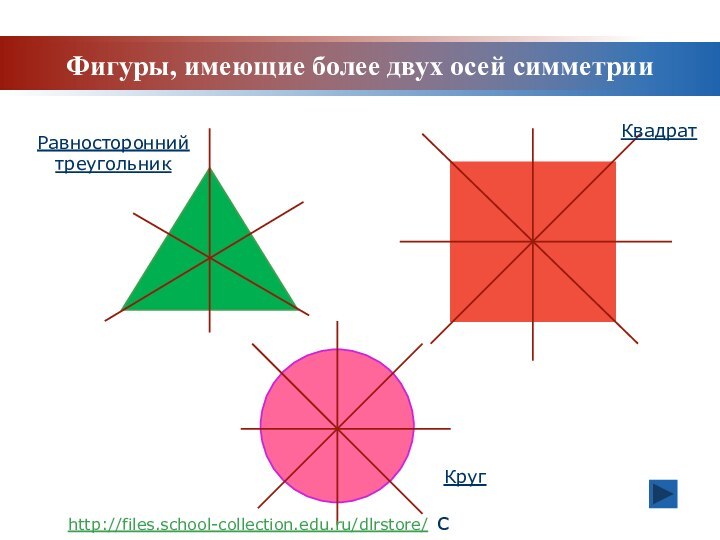
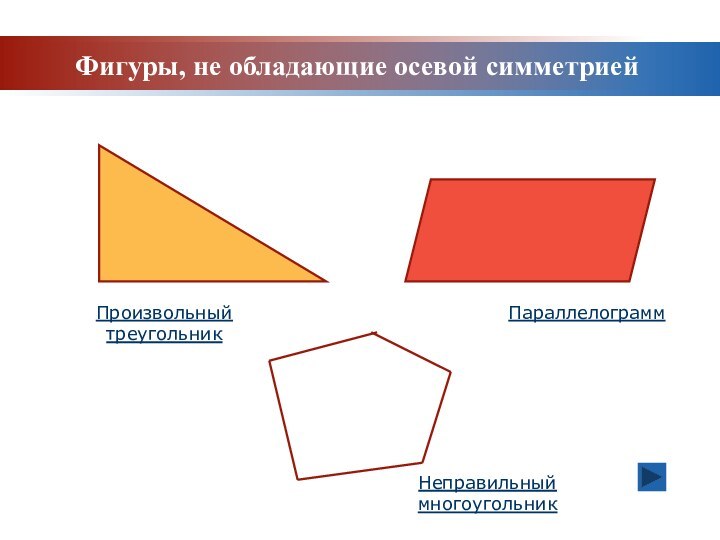
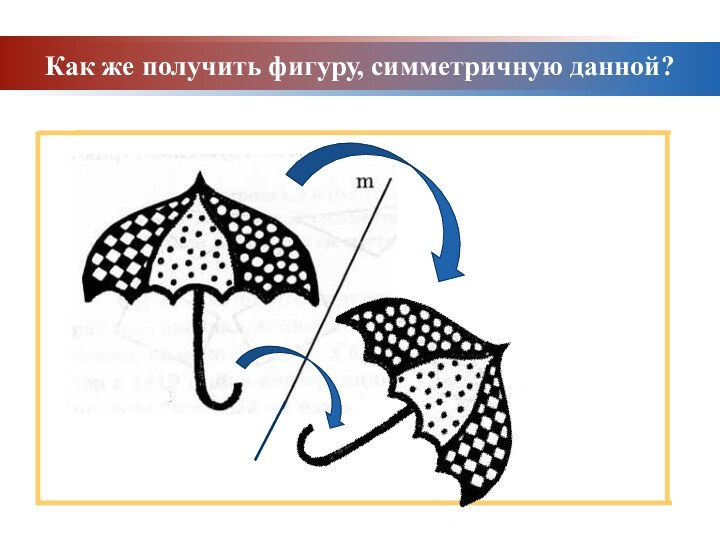

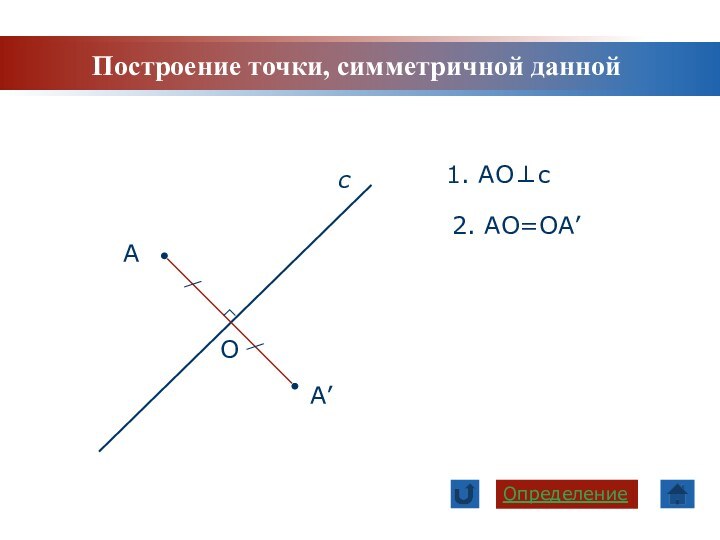
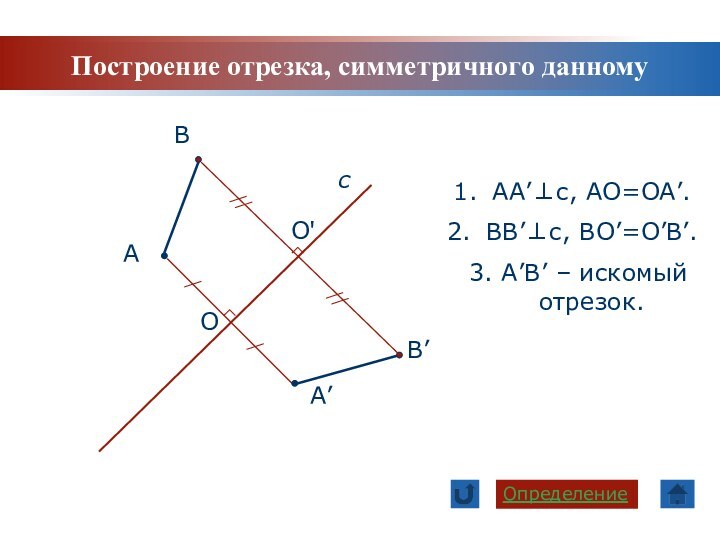
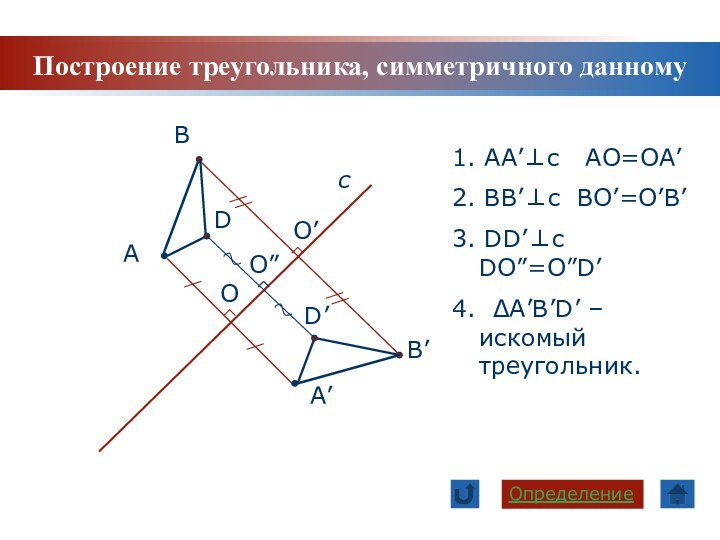
















Задачи урока:
http://files.school-collection.edu.ru/dlrstore/
а
Задачи
Задачи
Задачи
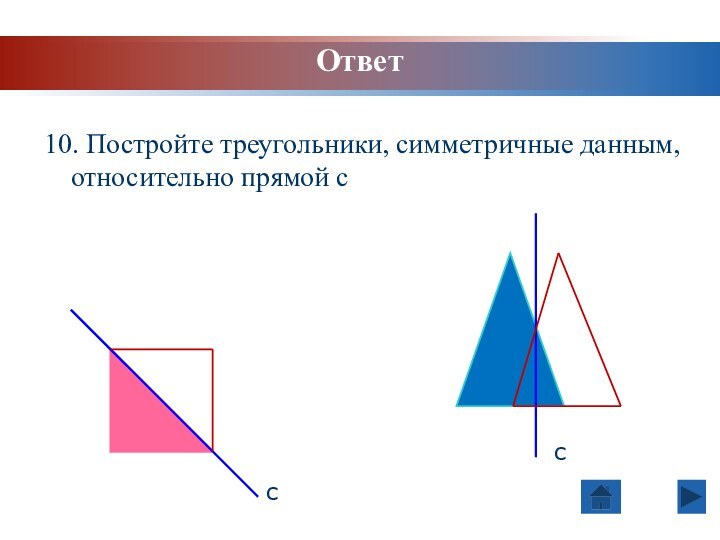
Ответ
Проверь себя
Задачи
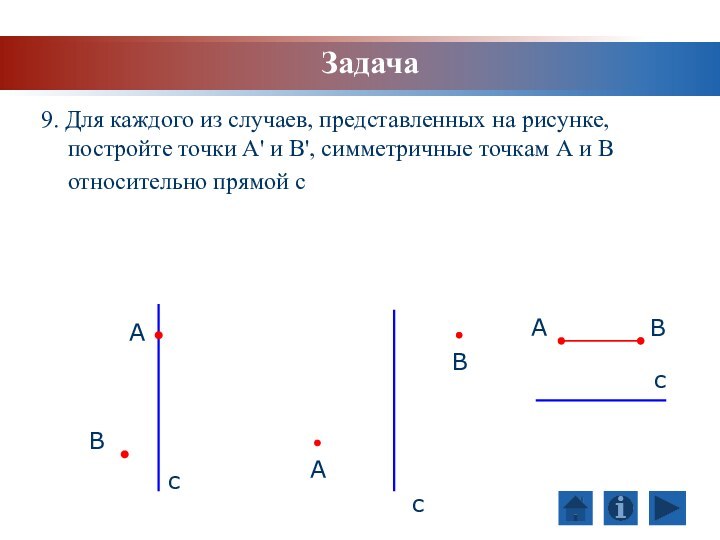
В
А
с
А
В
с
А
В
с
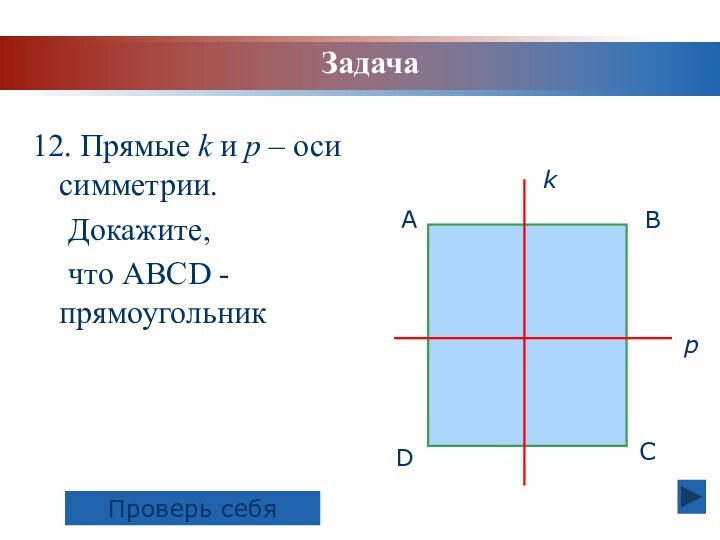
Задача
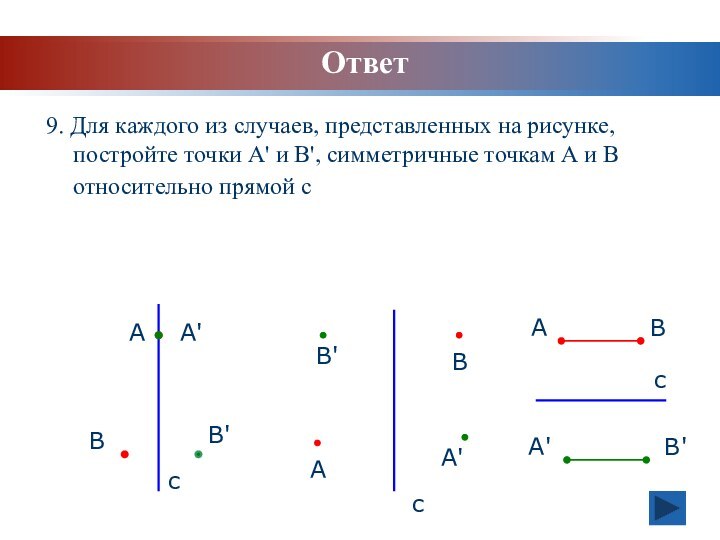
В
В'
А
А'
с
А
А'
В
В'
с
А
В
с
А'
В'
Ответ
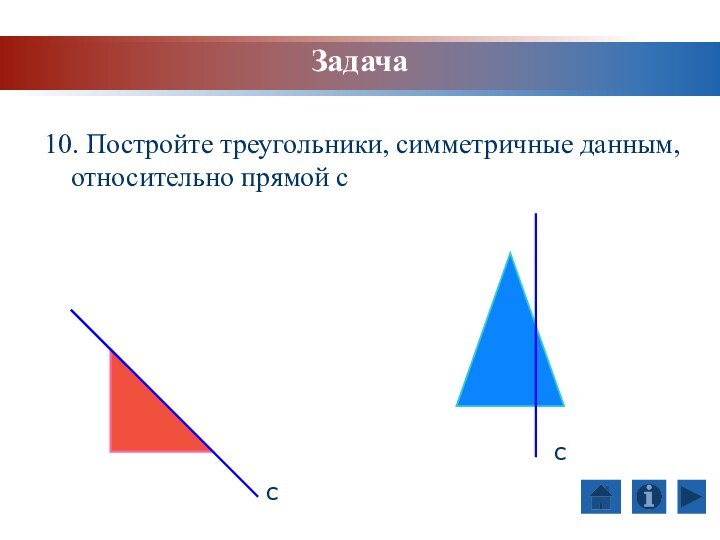
Задача