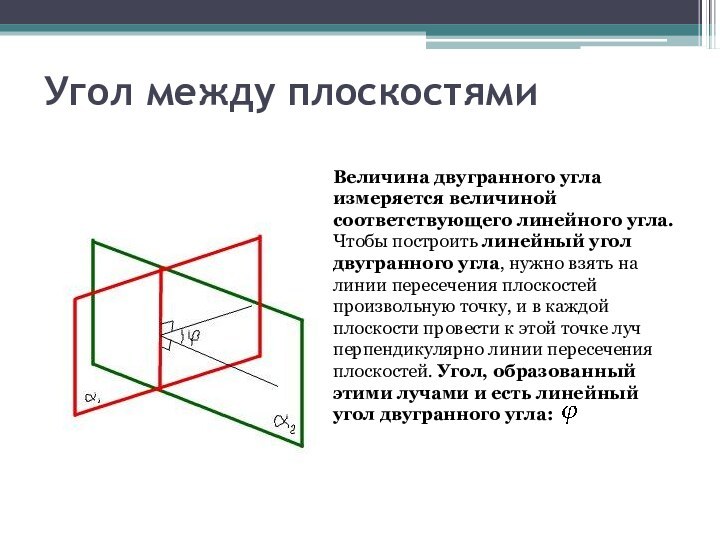
уравнении плоскости коэффициенты – координаты вектора нормали к плоскости
(то есть вектора, перпендикулярного плоскости).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







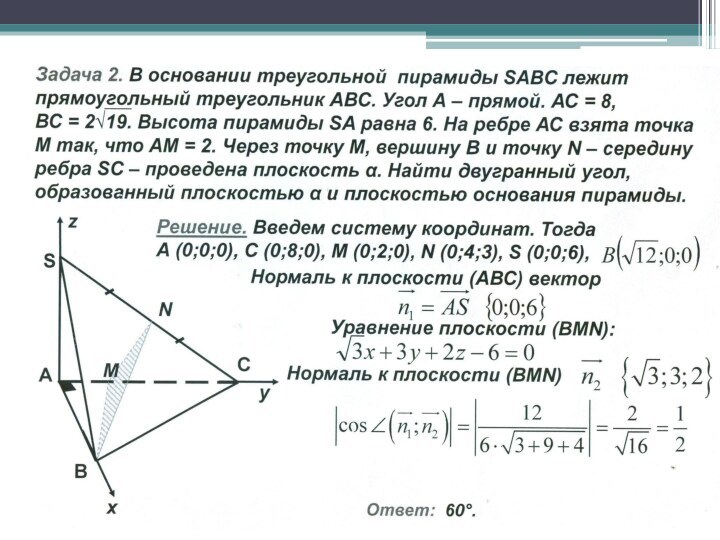


Решение.
Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1).
Решая систему
составляем уравнение плоскости (АD1E): x+2y-z=0.
2) плоскость CFD1:
отсюда находим уравнение 2x+y+z-3=0. Найдём искомый угол как угол между нормалями плоскостей.
, ,
откуда φ=60˚ Ответ: 60˚
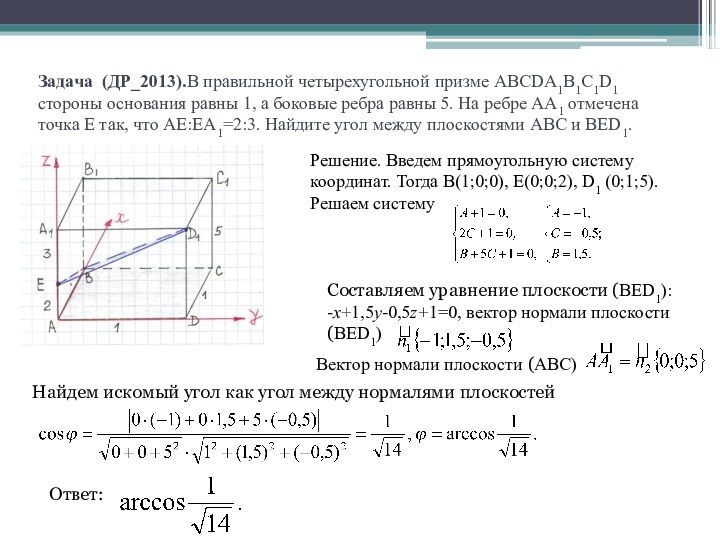
Решение. Введем прямоугольную систему координат. Тогда В(1;0;0), Е(0;0;2), D1 (0;1;5). Решаем систему
Составляем уравнение плоскости (ВЕD1):
-х+1,5у-0,5z+1=0, вектор нормали плоскости
(ВЕD1)
Вектор нормали плоскости (ABC)
Найдем искомый угол как угол между нормалями плоскостей
Ответ:
РЕШЕНИЕ. Введем прямоугольную систему координат,
поместив начало координат в точку А. Составим уравнение плоскости АКВ1. Точка А (0;0;0) принадлежит этой плоскости, то d=0.
Подставим координаты точек К(0;1; 0,5) и В1 (1;0;1)
в уравнение плоскости, получим b+c/2=0, a+c=0.
Таким образом имеем 2х+у - 2z=0.
Составим уравнение плоскости КМС.
Подставим координаты точек К(0;1; 0,5) и М (0,5;0;0),
С(1;1;0) в уравнение плоскости, получим систему:
Уравнение плоскости (КМС) принимает вид
и угол между плоскостями АВК1 и КМС находим из
2х – у +4z=1. Итак,