- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятие движения
Содержание
- 2. Понятие движения.
- 3. Цели урока:Рассмотреть осевую и центральную симметрии.Ввести понятие отображения плоскости на себя и движения.
- 4. Повторение. Осевая симметрия.Постройте точки симметричные А и В относительно прямой l.lAВА1В1АВА2
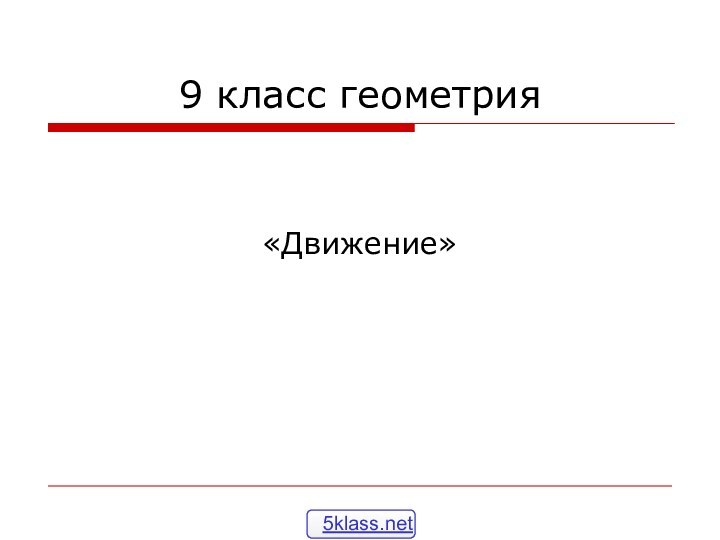
- 5. Повторение. Осевая симметрия.Постройте фигуры, симметричные данным относительно оси l.lFKLlCDNM
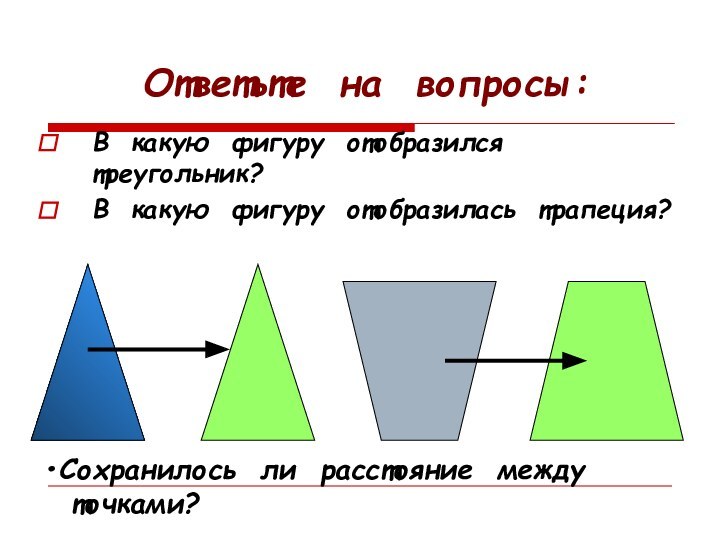
- 6. Ответьте на вопросы:В какую фигуру отобразился треугольник?В какую фигуру отобразилась трапеция?Сохранилось ли расстояние между точками?
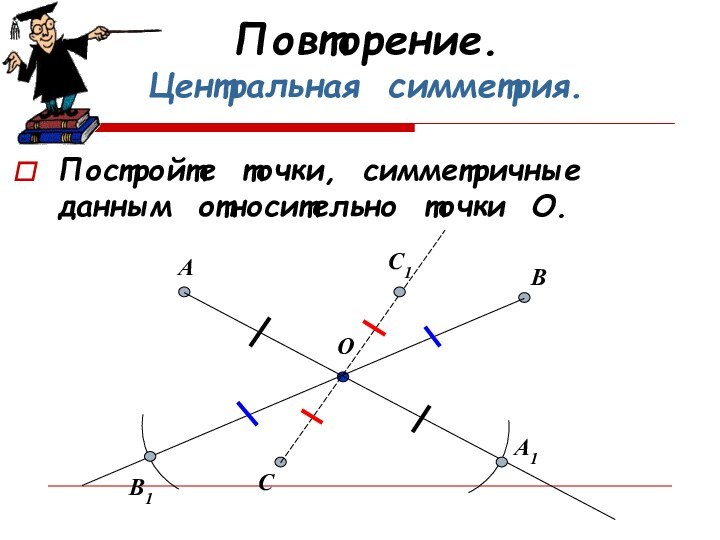
- 7. Повторение. Центральная симметрия.Постройте точки, симметричные данным относительно точки О. ОАВСА1В1С1
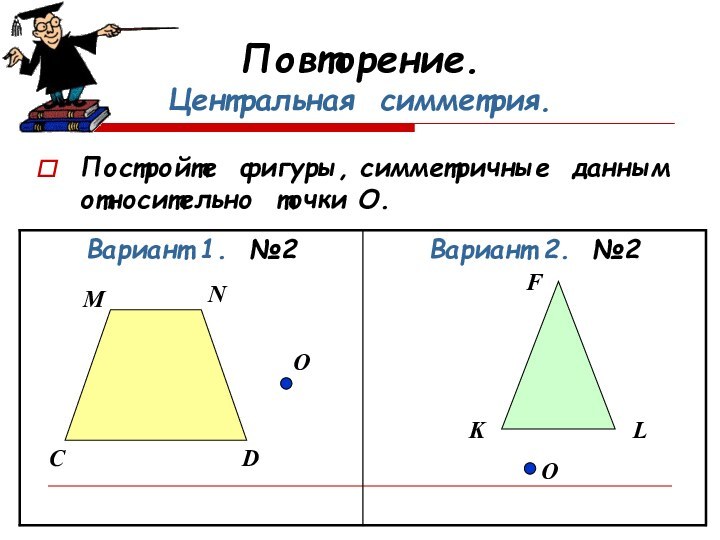
- 8. Повторение. Центральная симметрия.Постройте фигуры, симметричные данным относительно точки О.FKLCDNMОО
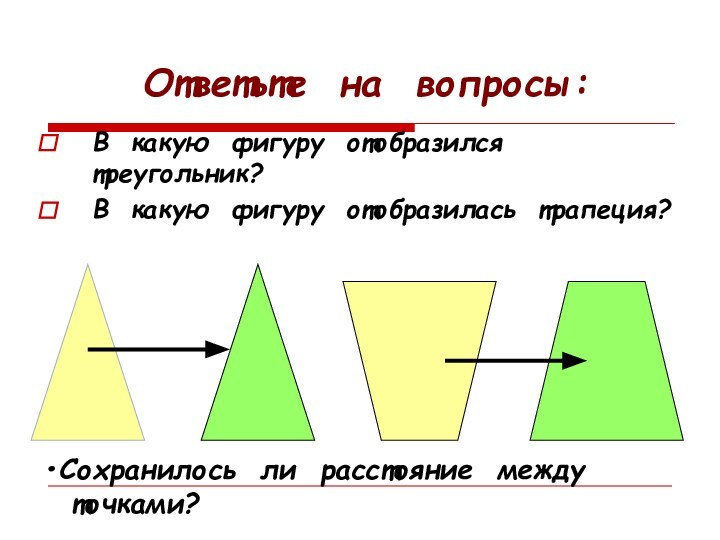
- 9. Ответьте на вопросы:В какую фигуру отобразился треугольник?В какую фигуру отобразилась трапеция?Сохранилось ли расстояние между точками?
- 10. Найдите соответствия:Каждой точке плоскости ставится в соответствие
- 11. Задача 1.Пусть М и N какие-либо точки,
- 12. Задача 1. Подсказки:Из точек N и N1
- 13. Задача 2. (№3)Докажите, что центральная симметрия есть
- 14. Скачать презентацию
- 15. Похожие презентации
Понятие движения.



Слайд 3
Цели урока:
Рассмотреть осевую и центральную симметрии.
Ввести понятие отображения
плоскости на себя и движения.
Слайд 4
Повторение.
Осевая симметрия.
Постройте точки симметричные А и В относительно
прямой l.
l
A
В
А1
В1
А
В
А2
Слайд 5
Повторение.
Осевая симметрия.
Постройте фигуры, симметричные данным относительно оси l.
l
F
K
L
l
C
D
N
M
Слайд 6
Ответьте на вопросы:
В какую фигуру отобразился треугольник?
В какую
фигуру отобразилась трапеция?
Сохранилось ли расстояние между
точками?
Слайд 7
Повторение.
Центральная симметрия.
Постройте точки, симметричные данным относительно точки О.
О
А
В
С
А1
В1
С1
Слайд 8
Повторение.
Центральная симметрия.
Постройте фигуры, симметричные данным относительно точки О.
F
K
L
C
D
N
M
О
О
Слайд 9
Ответьте на вопросы:
В какую фигуру отобразился треугольник?
В какую
фигуру отобразилась трапеция?
Сохранилось ли расстояние между
точками?
Слайд 10
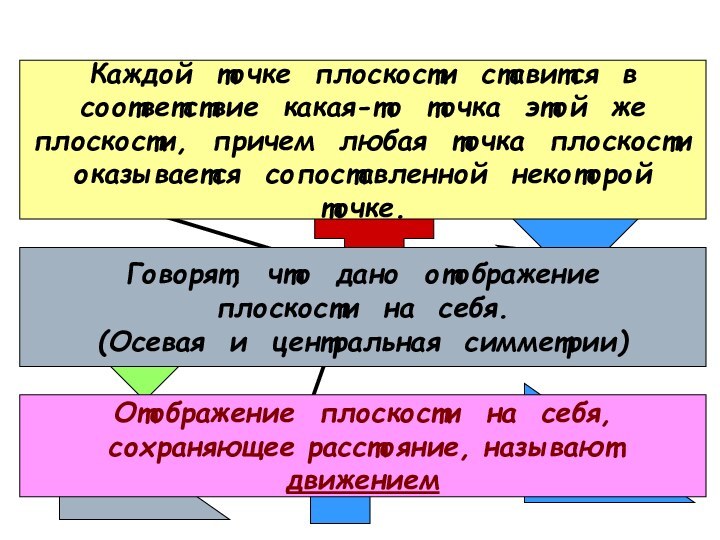
Найдите соответствия:
Каждой точке плоскости ставится в
соответствие какая-то
точка этой же
плоскости, причем любая точка плоскости
оказывается сопоставленной
некоторой точке.Говорят, что дано отображение
плоскости на себя.
(Осевая и центральная симметрии)
Отображение плоскости на себя,
сохраняющее расстояние, называют движением
Слайд 11
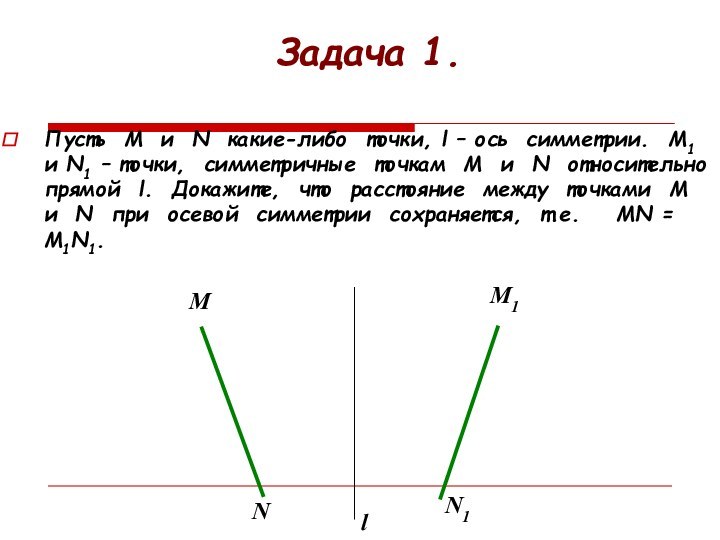
Задача 1.
Пусть М и N какие-либо точки, l
– ось симметрии. М1 и N1 – точки, симметричные
точкам М и N относительно прямой l. Докажите, что расстояние между точками М и N при осевой симметрии сохраняется, т.е. МN = M1N1.l
M
N
M1
N1
Слайд 12
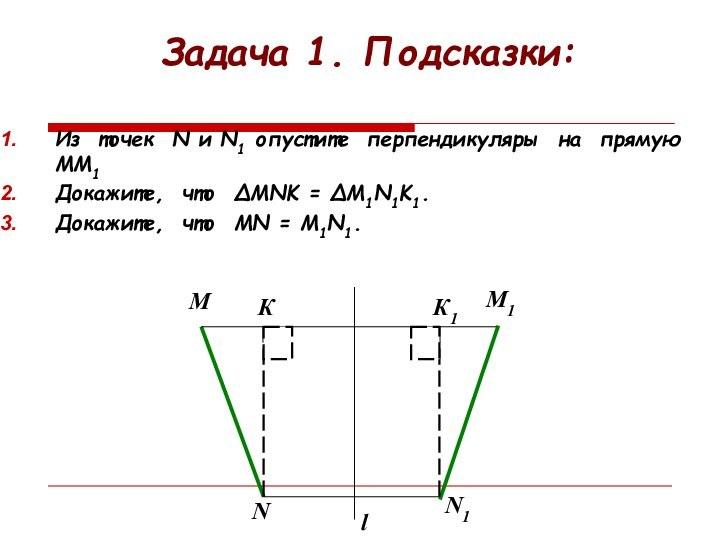
Задача 1. Подсказки:
Из точек N и N1 опустите
перпендикуляры на прямую ММ1
Докажите, что ∆MNK = ∆M1N1K1.
Докажите, что
МN = М1N1.l
M
N
M1
N1
К
К1
Слайд 13
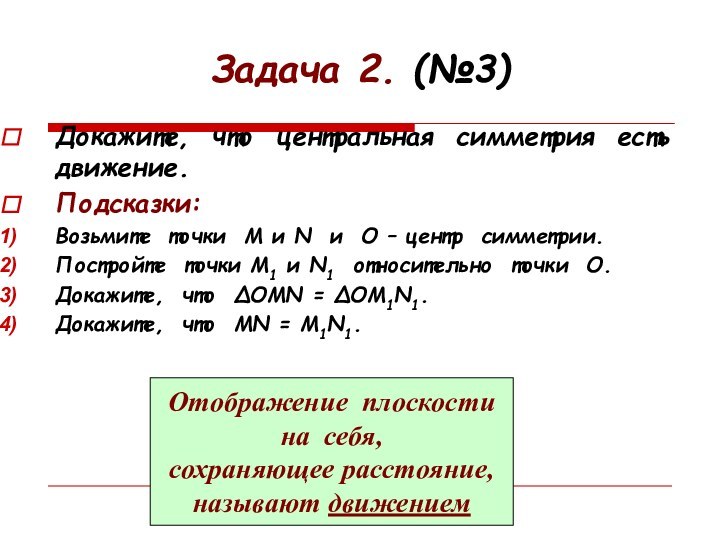
Задача 2. (№3)
Докажите, что центральная симметрия есть движение.
Подсказки:
Возьмите точки М и N и О – центр
симметрии. Постройте точки М1 и N1 относительно точки О.
Докажите, что ∆ОМN = ∆OM1N1.
Докажите, что МN = M1N1.
Отображение плоскости
на себя,
сохраняющее расстояние,
называют движением