Презентация на тему Замысловатые маршруты и правила Эйлера

отделённые друг от друга
а, b, с, d, e, f,

g – мосты

А, В, С, D – узлы(вершины)
а, b, с, d, e, f, g – ветви(ребра)

Чётный узел-узел, в котором сходится чётное число ветвей; нечётный узел-узел, в котором сходится нечётное число ветвей.

одним маршрутом, то она называется уникурсалъной сетью, а маршрут

— уникурсальным обходом.
Правила Эйлера:
1. Сеть, не имеющая нечетных узлов, допускает замкнутый уникурсальный обход с началом в любой точке сети.
2. Сеть, имеющая два и только два нечетных узла, обходится уникурсально, если начать движение с одного нечетного узла и закончить его в другом.
3. Сеть, имеющая больше двух нечетных узлов, нельзя полностью обойти одним маршрутом.

не проводя более одного раза по одной и той

же линии и почему?
Ответ: а, б.

науки в Санкт-Петербурге посетителям показывали схему мостов города
Требовалось

обойти все 17 мостов, соединяющих острова и берега Невы, на которых расположен Санкт-Петербург, Обойти надо так, чтобы каждый мост был пройден один раз.
Докажите, что требуемый уникурсальный обход всех мостов Санкт-Петербурга того времени возможен, но не может быть замкнутым, т.е. оканчиваться в пункте, от которого начинался.
Однако на своей копии рисунка вы сможете разработать и замкнутый обход, если позволите себе пройти дважды по каким-то двум мостам.

обхода семнадцати мостов. Но если разрешено пройти дважды по

каким-нибудь двум мостам, то возможен, например, маршрут, показанный на рис.

портретов Эйлера. Художник воспроизвел его одним росчерком пера (только

волосы нарисованы отдельно). Где на рисунке расположены начало и конец уникурсального контура? Повторите движение пера художника (волосы и пунктирные линии на рисунке не включаются в маршрут обхода).

очень хорошо знакомых состоялось много приветственных рукопожатий. Некоторые из

нас пожали четное число рук, другие — нечетное. Например, я обменялся тремя рукопожатиями, а мой друг, математик, — девятью. Когда я сказал своему другу, что обменявшихся нечетным числом рукопожатий, кроме меня и его, было еще 5 человек, он ответил:
— Ошибаешься. Число людей, пожавших нечетное число рук, непременно должно быть четным.
Прав ли он?

Решение.
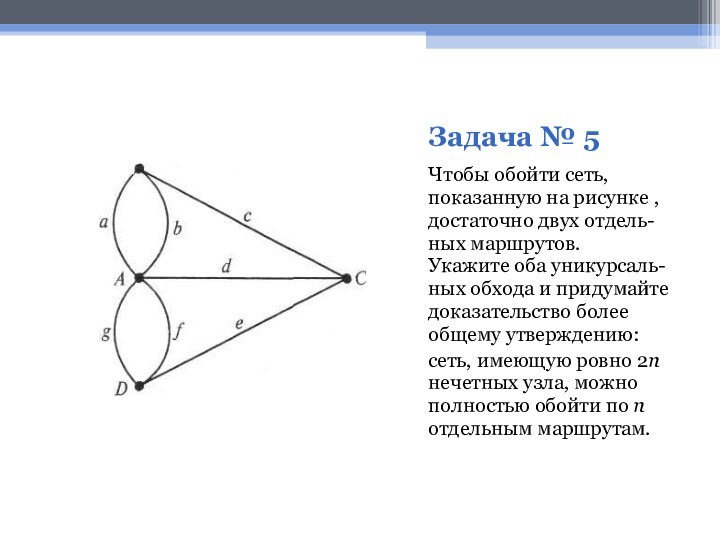
Да, прав. Задачу можно интерпретировать с сетью с числом узлов, равным числу людей, обменявшихся рукопожатием, а каждое рукопожатие рассматривать как ветвь, соединяющую 2 узла. Необходимо доказать, что в любой сети число узлов чётно.
Пусть сеть имеет r ветвей, у к-ых всего 2r концов. Пусть а1 –число узлов, от к-ых отходит 1 ветвь, a2 - число узлов, от к-ых отходит 2 ветви, аналогично получаем числа: a3,a4,…,an,…
Тогда,a1 узлов содержит a1 концов,a2 узлов - 2a2 концов, a3 узлов – 3a3 концов и т.д.Всего концов будет:
a1+2a2+3a3+…+nan+…=2r
Значит, a1+3a3+5a5+… чётно, а потому a1+a3+a5+…чётно, что и требовалось доказать.

, достаточно двух отдель-ных маршрутов.

Укажите оба уникурсаль-ных обхода и придумайте доказательство более общему утверждению:
сеть, имеющую ровно 2n нечетных узла, можно полностью обойти по п отдельным маршрутам.

АС. Если эту ветвь исключить из сети, то узлы

А и С становятся чётными и в сети остаются только два чётных угла: В и D. Значит, обход этой сети возможен с началом, например, в В и концом в D. Это второй маршрут.

тех пор, пока не достигнем узла,из которого уже нет

выхода. Тогда этот второй узел обязательно нечётный: из чётного узла всегда есть выход, а проходя нечётный узел, мы используем первый из сходящихся в нём концов для входа,а второй для выхода; когда же мы заканчиваем маршрут в нечётном узле, захватывается только один конец. сли изъять из сети пройденный маршрут, останется сеть с 2n — 2 нечетными узлами. Следовательно, если осуществить п аналогичных отдельных обходов, то останется одна или более сетей, все узлы которых четны. Но каждая из этих сетей имеет общий узел с одним из пройденных маршрутов и, следовательно, может быть включена в соответствующий маршрут. Таким образом, для полного обхода всей сети понадобится ровно п отдельных маршрутов. Отсюда следует, что если число нечетных узлов больше двух, то сеть нельзя обойти полностью одним маршрутом.Таким образом, мы попутно доказали справедливость правила 3 Эйлера.