Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре 10 кл по теме Логарифмическая функция

Содержание

Логарифмическая функцияа – заданное число, а>0, а≠1 РАВЕНСТВА ВЫРАЖАЮТ ОДНУ И ТУ ЖЕ ЗАВИСИМОСТЬ
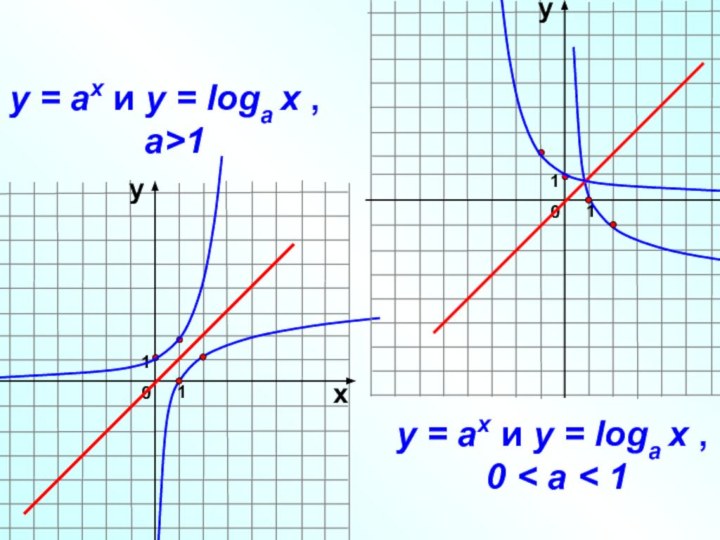
Логарифмическая функция, её свойства и график.Алгебра 10 класс Логарифмическая функцияа – заданное число, а>0, а≠1 РАВЕНСТВА ВЫРАЖАЮТ ОДНУ И ТУ ЖЕ ЗАВИСИМОСТЬ a > 1 Область определения: (0; +∞); Множество значений: (-∞, Свойства функции 0 < a < 1 Область определения: Основные свойства логарифмической функции 10ху110ху1у = аx и у = loga х , a>1у = аx y0 1 2 3 4 5 6 y0 1 2 3 4 5 6 1. Найдите область определения функции:1) у = log0,3 х 2) у 2. При каких значениях х имеет смысл функция: 1) у = log3 3. 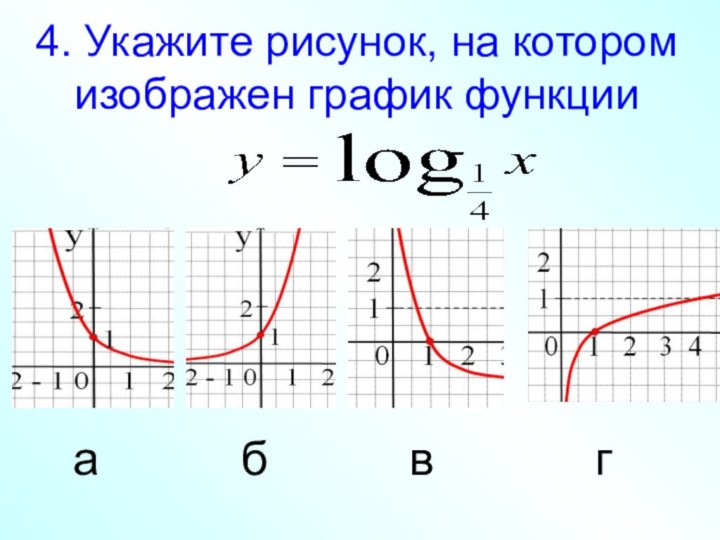Какие из функций являются возрастающими?а) у =log5 х в) у = logπ х б)г) 4. Укажите рисунок, на котором изображен график функции абвг 5. Какие точки принадлежат графику функции АВС(5;-1) 6. Сравните числа: 7. Установите знак выражения: (1;0); log2х0(1/16;4);(2;1); (2;-1); (4;2); (4;-2); (1/8;3); РефлексияО чем вы не имели представления до сегодняшнего урока, и что теперь
Слайды презентации

Слайд 2 Логарифмическая функция





а – заданное число, а>0, а≠1
 
РАВЕНСТВА ВЫРАЖАЮТ

Логарифмическая функцияа – заданное число, а>0, а≠1 РАВЕНСТВА ВЫРАЖАЮТ ОДНУ И ТУ ЖЕ ЗАВИСИМОСТЬ

ОДНУ И ТУ ЖЕ ЗАВИСИМОСТЬ

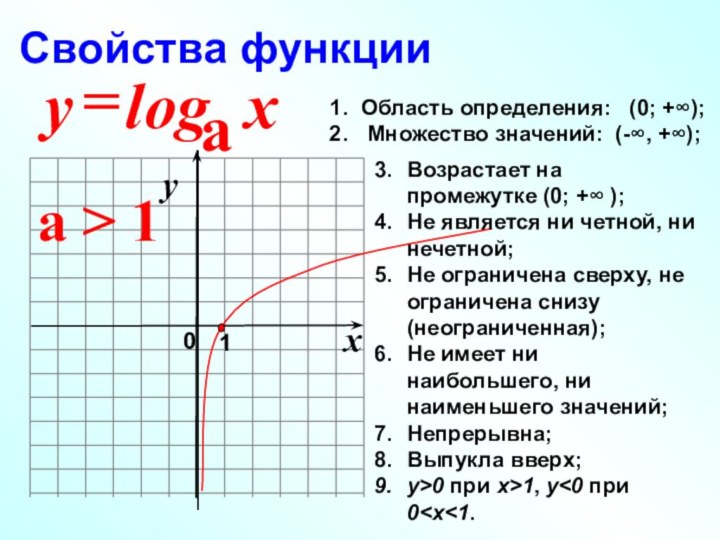
Слайд 3 a > 1
Область определения: (0; +∞);

a > 1 Область определения: (0; +∞); Множество значений: (-∞, +∞);Возрастает


Множество значений: (-∞, +∞);
Возрастает на промежутке (0; +∞

);
Не является ни четной, ни нечетной;
Не ограничена сверху, не ограничена снизу (неограниченная);
Не имеет ни наибольшего, ни наименьшего значений;
Непрерывна;
Выпукла вверх;
у>0 при х>1, у<0 при 0<х<1.

Свойства функции

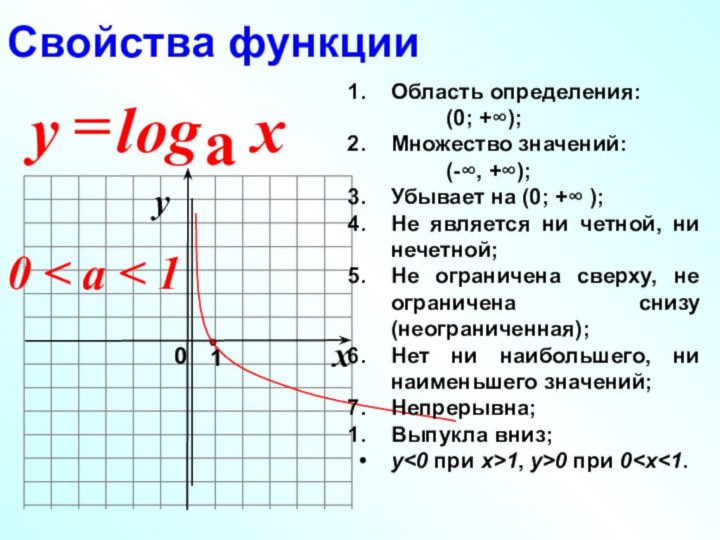
Слайд 4 Свойства функции
0 < a < 1

Область

Свойства функции 0 < a < 1 Область определения:

определения:
(0;

+∞);
Множество значений:
(-∞, +∞);
Убывает на (0; +∞ );
Не является ни четной, ни нечетной;
Не ограничена сверху, не ограничена снизу (неограниченная);
Нет ни наибольшего, ни наименьшего значений;
Непрерывна;
Выпукла вниз;
у<0 при х>1, у>0 при 0<х<1.

Слайд 5 Основные свойства логарифмической функции

Основные свойства логарифмической функции

Слайд 6


































1
0
х
у

1







































1
0
х
у

1






у = аx и у = loga х

10ху110ху1у = аx и у = loga х , a>1у =

,
a>1
у = аx и у = loga х

,
0 < a < 1

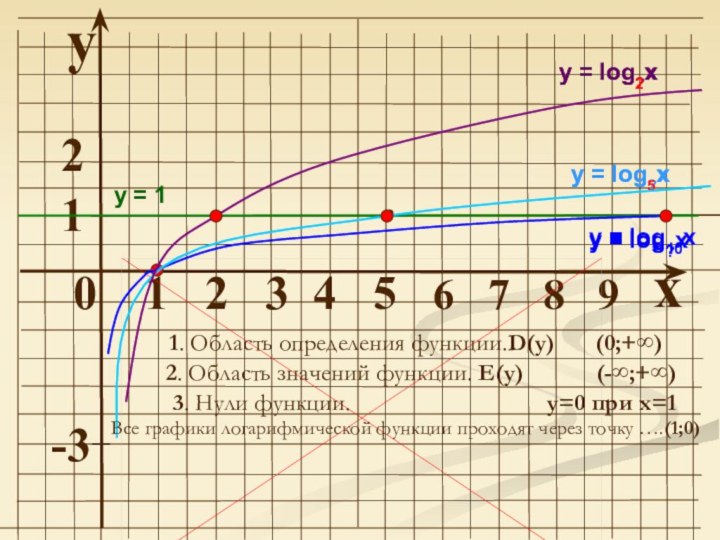
Слайд 7
y
0 1 2 3 4

y0 1 2 3 4 5 6 7 8 9 у

5 6 7 8

9

у = log?x

у = log?x

x



у = log?x

2


1

у = lоg10x

у = log5x

у = log2x

-3

у = 1

1. Область определения функции.D(y)

(0;+∞)

2. Область значений функции. Е(у)

(-∞;+∞)

3. Нули функции.

у=0 при х=1

Все графики логарифмической функции проходят через точку ….(1;0)


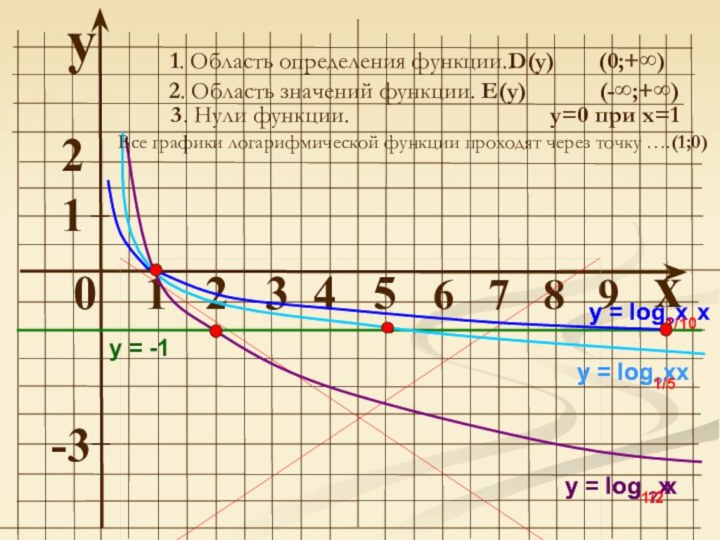
Слайд 8 y
0 1 2 3 4

y0 1 2 3 4 5 6 7 8 9 у

5 6 7 8

9

у = log?x

у = log ?x

x



у = log?x

2

1

у = lоg1/10x

у = log1/5x

у = log1/2x

-3

у = -1


1. Область определения функции.D(y)

(0;+∞)

2. Область значений функции. Е(у)

(-∞;+∞)

3. Нули функции.

у=0 при х=1







Все графики логарифмической функции проходят через точку ….(1;0)

Слайд 9 1. Найдите область определения функции:
1) у = log0,3

1. Найдите область определения функции:1) у = log0,3 х 2) у

х
2) у = log2 (х-1)
3)

у = log3 (3-х)

Ответы

(0; +∞)

(1;+∞)

(-∞; 3)

Слайд 10 2. При каких значениях х имеет смысл функция:

2. При каких значениях х имеет смысл функция: 1) у =

1) у = log3 х2 2) у =

log5 (-х) 3) у = lg │х│

х≠0

х≠0

x<0

Слайд 11 3. Какие из функций являются возрастающими?
а) у =log5

3. Какие из функций являются возрастающими?а) у =log5 х в) у = logπ х б)г)

х
в) у = logπ х
б)
г)

Слайд 12 4. Укажите рисунок, на котором изображен график функции

4. Укажите рисунок, на котором изображен график функции абвг


а
б
в
г

Слайд 13 5. Какие точки принадлежат графику функции
А
В


С(5;-1)

5. Какие точки принадлежат графику функции АВС(5;-1)

Слайд 14 6. Сравните числа:

6. Сравните числа:

Слайд 15 7. Установите знак выражения:

7. Установите знак выражения:

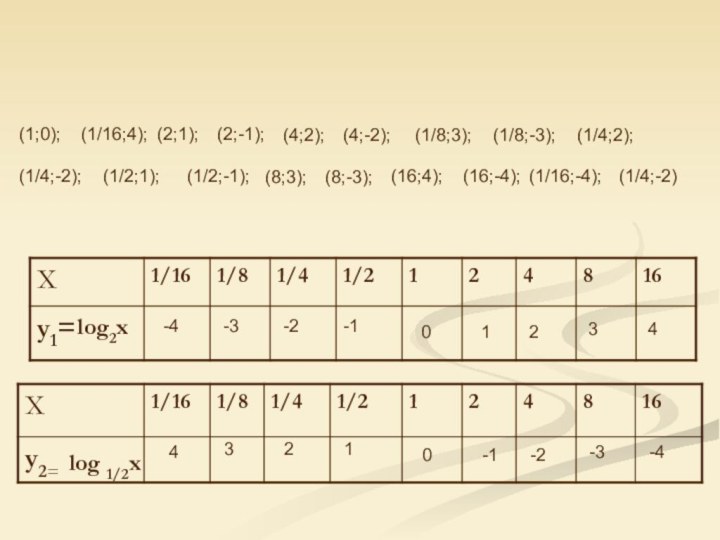
Слайд 16 (1;0);
log2х
0
(1/16;4);
(2;1);
(2;-1);
(4;2);

(1;0); log2х0(1/16;4);(2;1); (2;-1); (4;2); (4;-2); (1/8;3); (1/8;-3); (1/4;2); (1/4;-2); (1/2;1); (1/2;-1);


(4;-2);
(1/8;3);
(1/8;-3);
(1/4;2);
(1/4;-2);
(1/2;1);


(1/2;-1);

(8;3);

(8;-3);

(16;4);

(16;-4);

(1/16;-4);

(1/4;-2)

log 1/2х

4

-4

-3

-2

-1


1

2

3

4

0

3

2

1

-1

-2

-3

-4

Слайд 17 Рефлексия
О чем вы не имели представления до сегодняшнего

РефлексияО чем вы не имели представления до сегодняшнего урока, и что

урока, и что теперь вам стало ясно?
Что нового вы

узнали о логарифмической функции и ее приложениях?
С какими трудностями вы столкнулись при выполнении заданий?
Выделите тот вопрос, который для вас оказался менее понятным.
Какая информация вас заинтересовала?
Составьте синквейн «логарифмическая функция»
Оцените работу своей группы

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

  • Имя файла: prezentatsiya-po-algebre-10-kl-po-teme-logarifmicheskaya-funktsiya.pptx
  • Количество просмотров: 164
  • Количество скачиваний: 0
- Предыдущая Презентация по башкирскому языку Башҡортостандың юбилярҙары
Следующая - Презентация Великий шелковый путь

Похожие презентации

Презентация к занятиям по внеурочной деятельности по теме Принцип крайнего Презентация к занятиям по внеурочной деятельности по теме Принцип крайнего 265
Презентация по алгебре на тему Иррациональные уравнения Презентация по алгебре на тему Иррациональные уравнения 181
Презентация Брейн-ринг по алгебре Итоговое повторение Презентация Брейн-ринг по алгебре Итоговое повторение 165
Презентация по алгебре в 11 классе. Подготовка к ЕГЭ. Презентация по алгебре в 11 классе. Подготовка к ЕГЭ. 77
Прямоугольный треугольник Прямоугольный треугольник 156
Презентация к уроку по теме: Замена 5%, 10%, 20%, 25%, 50%, 75% обыкновенной дробью Презентация к уроку по теме: Замена 5%, 10%, 20%, 25%, 50%, 75% обыкновенной дробью 190
Презентация по математике: Тригонометрия. Фомулы двойного аргумента Презентация по математике: Тригонометрия. Фомулы двойного аргумента 167
Презентация по теме Теорема Пифагора Презентация по теме Теорема Пифагора 266
Презентация по алгебре Решение систем неравенств (9 класс) Презентация по алгебре Решение систем неравенств (9 класс) 166
Преобразование Фурье Преобразование Фурье 189
Площадь криволинейной трапеции( 11 класс ) Площадь криволинейной трапеции( 11 класс ) 157
Проект В мире вероятности Проект В мире вероятности 183
Презентация по алгебре и началам анализа на тему Тангенс и котангенс (10 класс) Презентация по алгебре и началам анализа на тему Тангенс и котангенс (10 класс) 172
Презентация по теме Иррациональные уравнения Презентация по теме Иррациональные уравнения 161
Великие математики Великие математики 184
Презентация к уроку Формула корней квадратного уравнения Презентация к уроку Формула корней квадратного уравнения 189
Презентация по математике на тему Прогрессии 9 класс Презентация по математике на тему Прогрессии 9 класс 167
Презентация по алгебре на тему Логарифмы Презентация по алгебре на тему Логарифмы 176
Презентация по алгебре и началам математического анализа 10 класс Показательная функция и её график Презентация по алгебре и началам математического анализа 10 класс Показательная функция и её график 140
Неполные квадратные уравнения Неполные квадратные уравнения 139
Презентация внеклассного мероприятия Считай, смекай, отгадывай! Презентация внеклассного мероприятия Считай, смекай, отгадывай! 162
Решение рациональных уравнений Решение рациональных уравнений 152
Презентация к уроку Простейшие логарифмические уравнения Презентация к уроку Простейшие логарифмические уравнения 182
Презентация к уроку на тему Неопределенный интеграл и его свойства Презентация к уроку на тему Неопределенный интеграл и его свойства 196
Презентация по алгебре на тему Умножение, деление и возведение дробей в степень 8 класс Презентация по алгебре на тему Умножение, деление и возведение дробей в степень 8 класс 207
Квадратный корень Квадратный корень 205
Презентация к уроку математике Задачи о Байкале Презентация к уроку математике Задачи о Байкале 189
Сокращение алгебраических дробей Сокращение алгебраических дробей 149
Презентация по математике на тему Числовые последовательности (9 класс) Презентация по математике на тему Числовые последовательности (9 класс) 199
Свойства функций Свойства функций 151