Презентация на тему по математике для 10 класса Преобразование тригонометрических выражений

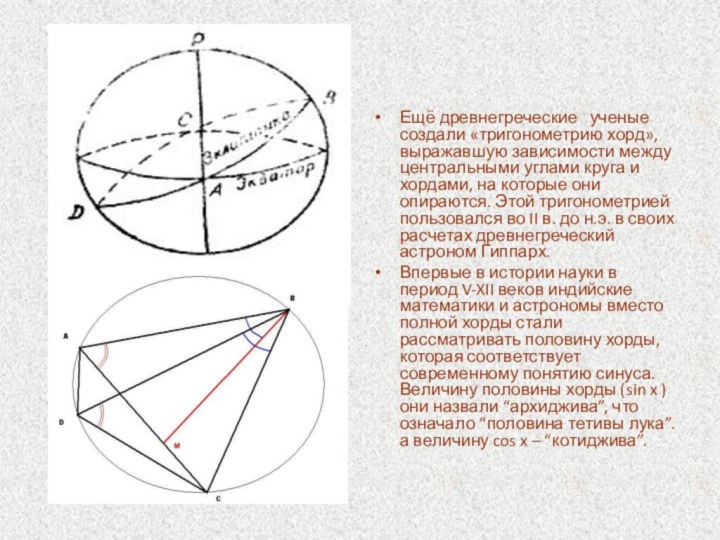
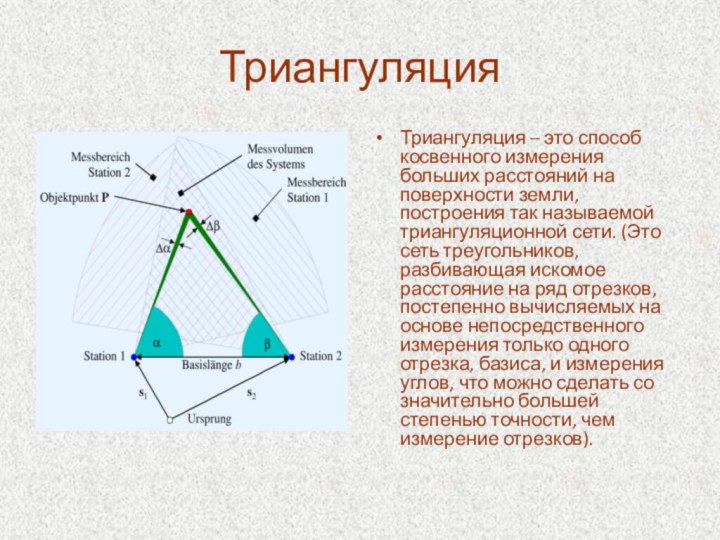
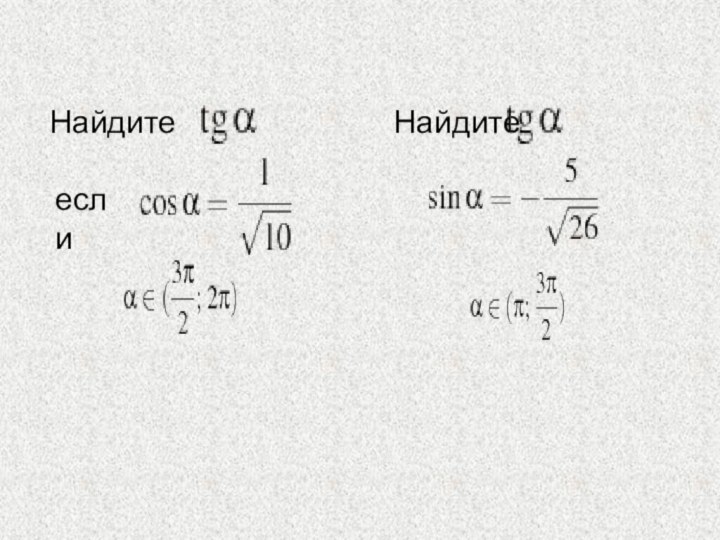необходимость тригонометрии в профессиях;
обобщить и систематизировать знания о тригонометрических

функциях и их преобразованиях;
развивать творческую активность;
расширять кругозор учащихся;
воспитывать товарищество и доброжелательность в общении.
Тип урока
комбинированный

итогов.
VI. Домашнее задание

математики, тригонометрия возникла в древние времена из потребностей людей

при ведении расчетов, связанных с земельными работами (для определения расстояния до недоступных предметов, составления географических карт и пр.).

зависимости между центральными углами круга и хордами, на которые

они опираются. Этой тригонометрией пользовался во II в. до н.э. в своих расчетах древнегреческий астроном Гиппарх.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды (sin x ) они назвали “архиджива”, что означало “половина тетивы лука”. а величину cos x – “котиджива”.

своей работе «Алмагест» («Великая книга») также вывел соотношения в

круге, которые по своей сути аналогичны современным формулам синуса половинного и двойного углов, синуса суммы и разности двух углов.

новое направление – аналитическое. Если до этого учения о

тригонометрических функциях строились на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно вошла в состав математического анализа и стала широко использоваться в механике и технике, особенно при рассмотрении колебательных процессов и иных периодических явлений.

знал ещё Ф. Виет. Швейцарский математик

И. Бернулли (1642-1727) в своих работах начал применять символику тригонометрических функций. Однако близкую к принятой теперь, ввел
Л. Эйлер в 1748 г. в своей работе «Введение в анализ бесконечных». В ней он рассмотрел вопрос о знаках всех тригонометрических функций любого аргумента.

на поверхности земли, построения так называемой триангуляционной сети. (Это

сеть треугольников, разбивающая искомое расстояние на ряд отрезков, постепенно вычисляемых на основе непосредственного измерения только одного отрезка, базиса, и измерения углов, что можно сделать со значительно большей степенью точности, чем измерение отрезков).

Снеллиус.

служит для: определения фигуры и размеров Земли методом градусных

измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.

деревянными или металлическими вышками высотой от 6 до 55

м в зависимости от условий местности

на местности закрепляются закладкой в грунт особых устройств в

виде металлических труб или бетонных монолитов с вделанными в них металлическими марками, фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.

право на три подсказки 1. пять игроков каждой команды поочередно

в устной форме выполняют задания (пять заданий по 5 баллов) 2.на доске выполняют задания из ЕГЭ следующие три игрока команды (три задания по 5 баллов) 3. на доске решают уравнения следующие два игрока.(два задания по 5 баллов) Максимальное количество баллов - 50

III.Практикум.

sin 300 cos π/3 tg π/4 ctg 900


arctg 1 arcsin ½ arcctg √3 arccos √3/2


arccos(- √2/2) arctg (-1)

ЕГЭ)

Найдите

если

4) Решите уравнение

а) √3cosx –

sinx=1

а) √3/2 cosx – ½ sinx = 1

б) sinx + sin3x + cosx + cos3x = 0

б) sin5x + sinx = 1-2sin2x

функции y = sin x и почему?
1. Чем дальше

в лес, тем больше дров.
2. Дальше кумы, меньше греха.
3. Кашу маслом не испортишь.
4. Выше меры конь не скачет.
5. Пересев хуже недосева.

Ответ: Выше меры конь не скачет.
Пояснение: если изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой “мерой”.

Л. Эйлер в 1748 г

– это способ косвенного измерения больших расстояний на поверхности

земли.
Триангуляцию впервые применил голландский ученый XVI в. В. Снеллиус