и определенного интеграла, свойства неопределенного и определенного интеграла, формулу
Ньютона-Лейбница. Ознакомиться с таблицей интегралов, понятием криволинейной трапеции и нахождением ее площади. Освоить навыки вычисления интеграла.Развивать познавательный интерес, логическое мышление, внимание. Формировать потребности в приобретении знаний.
Воспитывать ответственность, самостоятельность, культуру общения и учебного труда.
В результате проведения занятия студент должен:
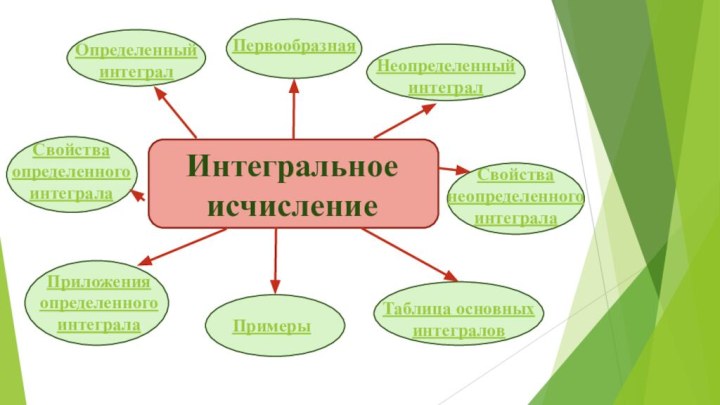
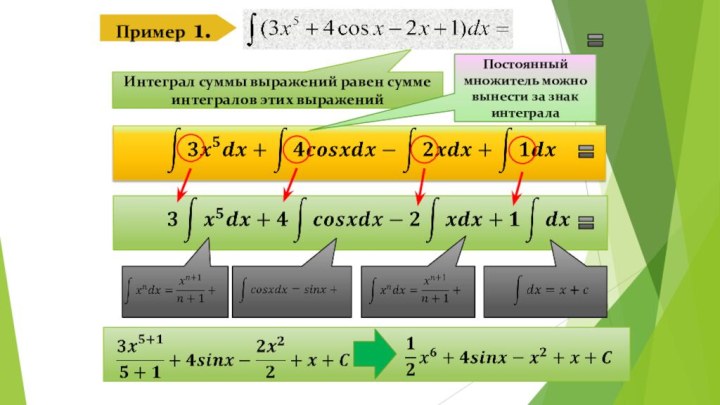
Знать основные понятия: неопределенный интеграл, свойства неопределенного интеграла (таблица интегралов), определенный интеграл, свойства определенного интеграла.
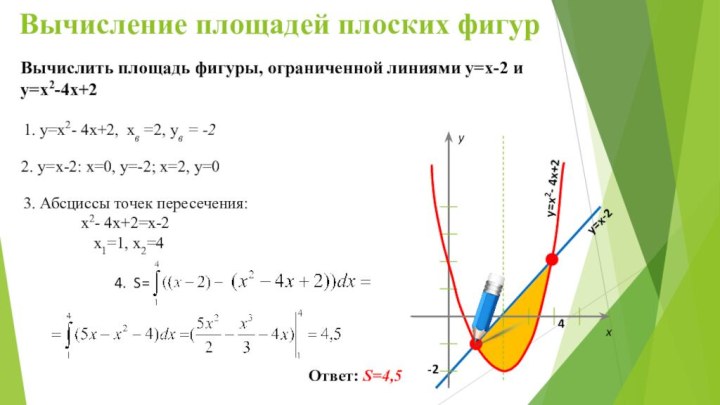
Уметь находить неопределенный и определенный интеграл.




















![Электронное пособие по математике Интегральное исчисление Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x),](/img/tmb/7/601417/42801fda3041f1f759acf632821b1394-720x.jpg)
![Электронное пособие по математике Интегральное исчисление Замечание: Если функция изменяет знак на промежутке [a;b] , тоГеометрический смысл определенного интеграла](/img/tmb/7/601417/3160edeebd04df92e1cff7cccbc9001b-720x.jpg)

![Электронное пособие по математике Интегральное исчисление Дан прямолинейный неоднородный стержень [0;6], его плотность в точке х определяется по](/img/tmb/7/601417/cfabd3ff8b3aaf0d8708b5ba017159b7-720x.jpg)