Слайд 2
Корень n-ой степени.
Ребята, тема сегодняшнего занятия корень n-ой
степени из действительного числа.
Корень квадратный из действительного числа,
мы с вами, изучали в 8 классе. Корень квадратный связан с функцией вида .Ребята вы помните, как мы вычисляли корни квадратные и какие у него были свойства? Повторите самостоятельно эту тему.
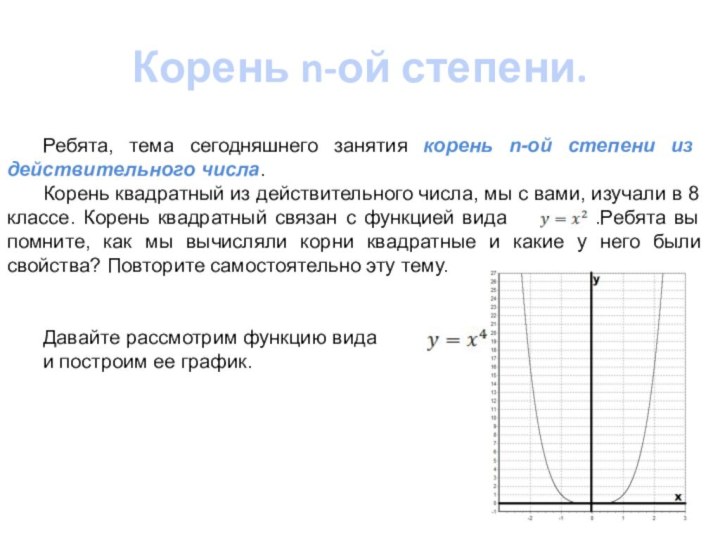
Давайте рассмотрим функцию вида
и построим ее график.
Слайд 3
Корень n-ой степени.
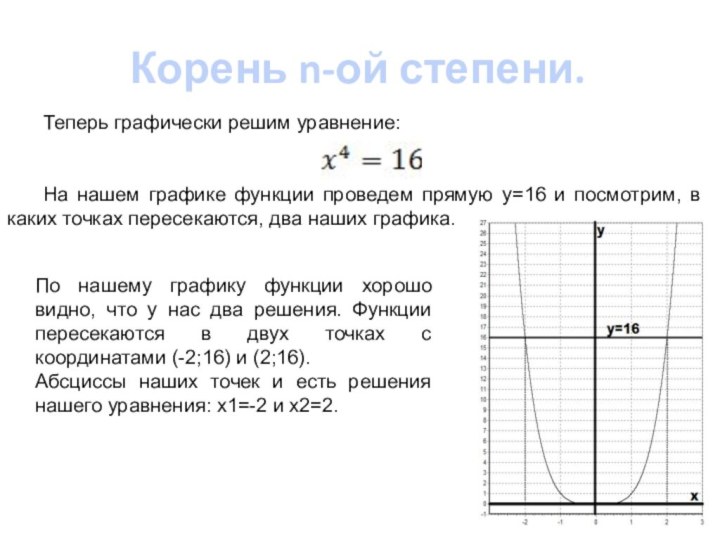
Теперь графически решим уравнение:
На нашем
графике функции проведем прямую y=16 и посмотрим, в каких
точках пересекаются, два наших графика.
По нашему графику функции хорошо видно, что у нас два решения. Функции пересекаются в двух точках с координатами (-2;16) и (2;16).
Абсциссы наших точек и есть решения нашего уравнения: x1=-2 и x2=2.
Слайд 4
Корень n-ой степени.
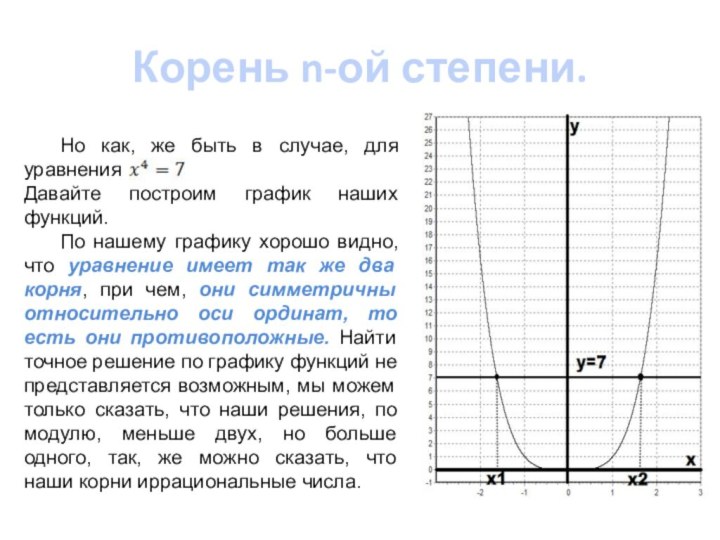
Но как, же быть в
случае, для уравнения
Давайте построим график наших функций.
По нашему
графику хорошо видно, что уравнение имеет так же два корня, при чем, они симметричны относительно оси ординат, то есть они противоположные. Найти точное решение по графику функций не представляется возможным, мы можем только сказать, что наши решения, по модулю, меньше двух, но больше одного, так, же можно сказать, что наши корни иррациональные числа.
Слайд 5
Корень n-ой степени.
Столкнувшись с такой проблемой, нужно было,
как то ее описать, математики ввели новое обозначение: ,
который, назвали корнем четвертой степени.
Так корни нашего уравнения запишутся вот в таком виде:
Читается как корень четвертой степени из семи.
В общем виде мы говорили об уравнении
где а>0 (а=1,7,16).
Вообще мы можем рассматривать уравнения вида:
где, а>0, n- любое натуральное число.
Слайд 6
Корень n-ой степени.
Нам, следует обратить внимание на степень
при х, от четности или нечетности степени - меняется
количество решений.
Давайте рассмотрим конкретный пример.
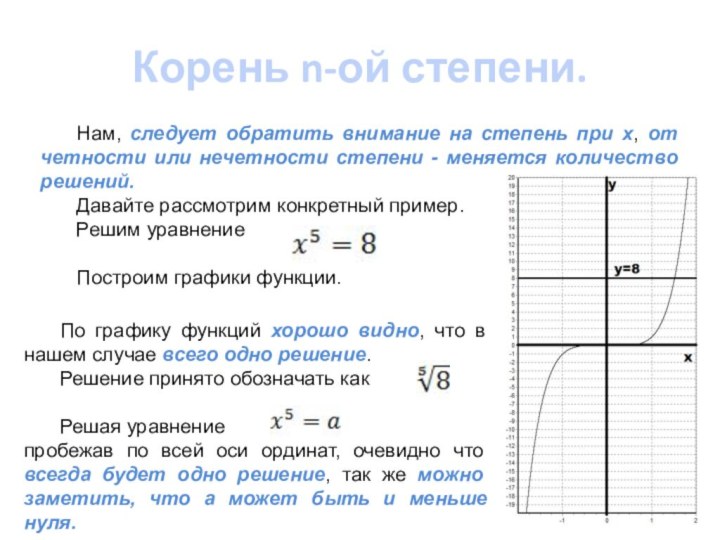
Решим уравнение
Построим графики функции.
По графику функций хорошо видно, что в нашем случае всего одно решение.
Решение принято обозначать как
Решая уравнение
пробежав по всей оси ординат, очевидно что всегда будет одно решение, так же можно заметить, что а может быть и меньше нуля.
Слайд 7
Корень n-ой степени.
Определение. Корнем n-ой степени из
неотрицательного числа а (n=2,3,4…), называют такое неотрицательное число, при
возведении которого в степень n получается число а.
Это число обозначают как
число а называется подкоренным число, n – показатель корня.
Корни второй и третьей степени принято называть корнями квадратными и кубическими соответственно. Мы их изучали в восьмом и девятом классе.
Если а≥0, n=2,3,4,5… то 1) 2)
Операцию нахождения корня из неотрицательного числа называют – извлечением корня.
Слайд 8
Корень n-ой степени.
Возведение в степень и извлечения корня
одна и та же зависимость:
Ребята, обратите внимание в таблице
только положительные числа, в определении мы оговорили, что корень извлекается только из неотрицательного числа а, дальше мы внесем уточнения, когда можно и из отрицательного.
Слайд 9
Корень n-ой степени.
Пример.
Вычислить:
а) б)
в)
г)
Решение:
а)
б)
в)
г) В данном примере мы точное значение узнать не можем, наше число иррациональное, но мы можем сказать, что оно больше двух и меньше трех, так как два в пятой степени равно 32, а три в пятой степени равно 243, 34 лежит между этим числами.
Приближенное значение мы можем найти с помощью калькулятора, который может вычислять корни
с точностью до тысячных.
Слайд 10
Корень n-ой степени.
В нашем определении мы договорились вычислять
корни n-ой степени только из положительных чисел, но мы
с вами уже видели пример, в начале урока, что их можно извлекать и из отрицательных чисел, мы с вами рассмотрели нечетный показатель функции, давайте внесем уточнения.
Определение. Корнем нечетной степени n из отрицательного числа а (n=3,5,7,9…) называют такое отрицательное число, при возведение которого в степень n получается а.
Обозначение принято использовать такие же.
Если а<0, n=3,5,7… то 1) 2)
Корень четной степени имеет смысл только для положительного подкоренного числа, корень нечетной степени имеет смысл для любого подкоренного числа.
Слайд 11
Корень n-ой степени.
Пример.
Решить уравнения:
а) б) в) г)
Решение:
а) Если
, то y=-27.
То есть, обе части нашего уравнения, нам надо возвести в куб. 3х+3=-27; 3х=-30; х=-10
б) Возведем обе части в четвертую степень:
2х-1=1; 2х=2; х=1
в) Согласно нашему определению, корень четной степени можно извлекать только из положительного числа, а нам дано отрицательное, тогда корней нет.
г) Возведем обе части уравнения в пятую степень: