- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математический язык. Математическая модель
Содержание
- 2. Цели:19.04.2012Дать понятие об уравнении и его корнях.Дать
- 3. 19.04.2012Одной из самых простых и важных математических
- 4. х + 2 = 5х = 3Уравнение.Корень
- 5. Найдём корень уравнения:х + 37 = 85х3785=_х
- 6. Не решая уравнений, проверь, какое из чисел является корнем уравнения.42;0;14;1287 + (32 – х) = 10519.04.2012
- 7. 42;0;14;1287 + (32 – 14) = 10587
- 8. Решим уравнение:(35 + у) – 15 =
- 9. 19.04.2012Каждое уравнение имеет одни и те же
- 10. 19.04.2012При решении уравнений используют свойства:Если в уравнении
- 11. Решите уравнение и выполните проверку: у -
- 12. Решите уравнение и выполните проверку:24 -
- 13. 19.04.2012 Решите уравнение и выполните проверку:45 +
- 14. 19.04.2012Уравнение вида: aх + b = 0
- 15. 19.04.2012 Решите уравнение : 2(3х - 1)
- 16. 19.04.2012уравнение имеет бесконечно много корней Решите уравнение
- 17. 19.04.2012Уравнение корней не имеет Решите уравнение :
- 18. 19.04.2012Вспомним!При решении задачи четко выполнены три этапа:Получение
- 19. 19.04.2012Задача:Три бригады рабочих изготавливают игрушки к Новому
- 20. 19.04.20122) Работа с математической моделью. х +
- 21. Скачать презентацию
- 22. Похожие презентации




















Слайд 2
Цели:
19.04.2012
Дать понятие об уравнении и его корнях.
Дать понятие
о линейном уравнении и его решении.
решение с помощью уравнений.
Слайд 3
19.04.2012
Одной из самых простых и важных математических моделей
реальных ситуаций есть линейные уравнения с одной переменной.
3х =
125у - 10 = 0
2а +7 = 0
Решить линейное уравнение с одной
переменной – это значит найти те значения
переменной, при каждом из которых
уравнение обращается в верное числовое
равенство.
Слайд 4
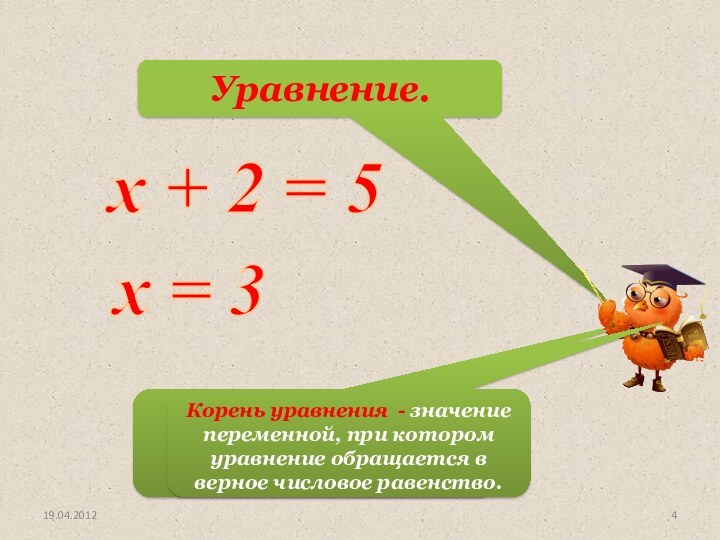
х + 2 = 5
х = 3
Уравнение.
Корень уравнения.
19.04.2012
Корень
уравнения - значение переменной, при котором уравнение обращается в
верное числовое равенство.
Слайд 5
Найдём корень уравнения:
х + 37 = 85
х
37
85
=
_
х =
48
Мы решили уравнение!
19.04.2012
Решили уравнение – нашли те значения переменной,
при котором уравнение обращается в верное числовое равенство.Слайд 6 Не решая уравнений, проверь, какое из чисел является
корнем уравнения.
42;
0;
14;
12
87 + (32 – х) = 105
19.04.2012
Слайд 7
42;
0;
14;
12
87 + (32 – 14) = 105
87 +
(32 – 42) = 77
87 + (32 – х)
= 10587 + (32 – 0) = 119
87 + (32 – 12) = 107
х = 14
19.04.2012
Слайд 8
Решим уравнение:
(35 + у) – 15 = 31
y
= 11
19.04.2012
35 + у
=
31
+
15
35 + у
=
46
y = 46 -35
Решить
уравнение – это значит найти все его корни или доказать, что их нет
Слайд 9
19.04.2012
Каждое уравнение имеет одни и
те же корни
х₁ = 2 х₂ = 3
Уравнения,
которые имеют одни ите же корни, называют
равносильными.
Слайд 10
19.04.2012
При решении уравнений используют
свойства:
Если в уравнении перенести
слагаемое из одной
части в другую, изменив его
знак, то получитсяравносильное уравнение.
2. Если обе части уравнения умножить или
разделить на число (не равное нулю), то
получится равносильное
уравнение.
Слайд 11
Решите уравнение и выполните проверку:
у - 35
+ 12 = 32;
у – 23 = 32;
у =
32 + 23;у = 55;
(55 - 35) + 12 = 32;
30 + 12 = 32;
32 = 32.
(у - 35) + 12 = 32;
Решение.
Ответ: 55.
19.04.2012
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями
Слайд 12
Решите уравнение и выполните проверку:
24 - 21
+ х = 10;
х + 3 = 10;
х = 10 - 3;
х = 7
(24 + 7) - 21 = 31 - 21 = 10;
Ответ: 7.
б) (24 + х) - 21 = 10;
Решение.
19.04.2012
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями
Слайд 13
19.04.2012
Решите уравнение и выполните проверку:
45 + 18
- у = 58;
63 - у = 58;
у =
63 - 58;у = 5
(45 - 5) + 18 = 40 + 18 = 58.
Ответ: 5.
Решение.
в) (45 - у) + 18 = 58;
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями
Слайд 14
19.04.2012
Уравнение вида:
aх + b = 0
называется линейным уравнением
с одной переменной (где х
– переменная,а и b некоторые числа).
Внимание!
х – переменная входит в уравнение
обязательно в первой степени.
Слайд 15
19.04.2012
Решите уравнение :
2(3х - 1) =
4(х + 3)
Решение уравнений состоит в постепенной замене более
простыми равносильными уравнениями. aх + b = 0
Приведем к стандартному виду:
2(3х - 1) = 4(х + 3)
6х – 2 = 4х + 12
6х – 4х = 2 + 12
2х = 14
х = 14 : 2
х = 7
- уравнение имеет 1 корень
Слайд 16
19.04.2012
уравнение имеет бесконечно много корней
Решите уравнение :
2(3х - 1) = 4(х + 3) – 14
+ 2хПриведем к стандартному виду:
aх + b = 0
2(3х - 1) = 4(х + 3) – 14 + 2х
6х – 2 = 4х + 12 – 14 + 2х
6х – 4x - 2х = 2 + 12 – 14
0 · x = 0
При подстановке любого значения х получаем
верное числовое равенство:
0 = 0
x – любое число
(а = 0, b = 0)
Слайд 17
19.04.2012
Уравнение корней не имеет
Решите уравнение :
2(3х
- 1) = 4(х + 3) + 2х
Приведем к
стандартному виду: aх + b = 0
2(3х - 1) = 4(х + 3) + 2х
6х – 2 = 4х + 12 + 2х
6х – 4x - 2х -2 - 12 = 0
0 · x - 14 = 0
При подстановке любого значения х получаем
неверное числовое равенство:
-14 = 0
(а = 0, b = -14)
Слайд 18
19.04.2012
Вспомним!
При решении задачи четко выполнены три этапа:
Получение математической
модели.
Обозначают неизвестную в задаче величину буквой,
используя эту букву,
записывают другие величины,составляют уравнение по условию задачи.
2) Работа с математической моделью.
Решают полученное уравнение,
находят требуемые по условию задачи величины.
3) Ответ на вопрос задачи.
Найденное решение используют для ответа на вопрос задачи
применительно к реальной ситуации.
Математическая модель позволяет анализировать
и решать задачи.
Слайд 19
19.04.2012
Задача:
Три бригады рабочих изготавливают игрушки к Новому году.
Первая бригада
сделала шары. Вторая бригада изготавливает сосульки и
сделала их на 12 штук больше, чем шаров. Третья бригада изготавливает снежинки и сделала их на 5 штук меньше, чем изготовлено шаров и сосулек вместе. Всего было сделано 379 игрушек. Сколько в отдельности изготовлено шаров, сосулек и снежинок?Шары –
Сосульки –
Снежинки -
?
?
на 12 шт. больше, чем
?
?
- на 5 шт. меньше, чем
Получение математической модели.
Обозначим шары –
сосульки –
снежинки -
х (шт.)
х + 12 (шт.)
х + х + 12 = 2х + 12 (шт.)
2х + 12 – 5 = 2х + 7 (шт.)
Так как по условию всего было сделано 379 игрушек, то составим уравнение:
х + (х + 12) + (2х + 7) = 379
линейное уравнением с одной переменной
Слайд 20
19.04.2012
2) Работа с математической моделью.
х + (
х + 12) + (2х + 7) = 379
х + х + 12 + 2х + 7 = 379Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями.
Приведем к стандартному виду:
aх + b = 0
4х + 19 = 379
4х = 379 - 19
4х = 360
х = 360 : 4
х = 90
90 шт. - шаров
х + 12 = 90 + 12 = 102 (шт.) - сосульки
2х + 7 = 2 · 90 + 7 = 187 (шт.) - снежинок
3) Ответ на вопрос задачи:
90 шт. – шаров,
102 (шт.) – сосульки,
187 (шт.) - снежинок