- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему: Теорема Виета
Содержание
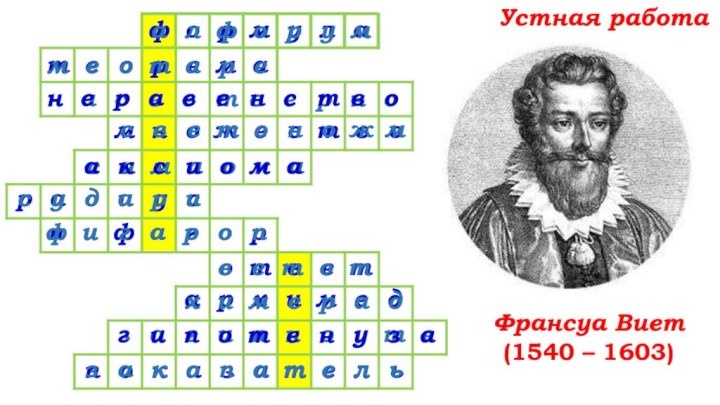
- 2. Устная работаФрансуа Виет(1540 – 1603)
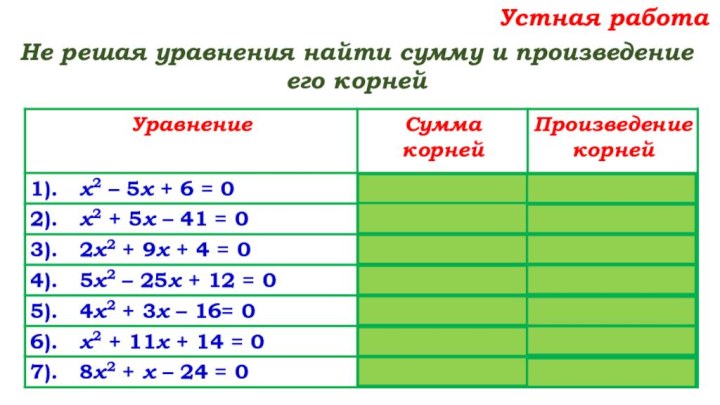
- 3. Устная работаНе решая уравнения найти сумму и произведение его корней
- 4. 27.01.16Теорема ВиетаАлгебра – 8 Урок № 57.2
- 5. Устная работа1). x1 + x2 = –
- 6. Устная работа1). х1 + х2 = –
- 7. Устная работа4). х1 + х2 =
- 8. 3х2 – 8х – 15 = 01).
- 9. 3х2 – 8х – 15 = 02).
- 10. 3х2 – 8х – 15 = 03).
- 11. 3х2 – 8х – 15 = 02).
- 12. 1). х2 – 7х + 12 =
- 13. 3). 5х2 + 3х – 2 =
- 14. Решение:x2 + 6x + q = 01).
- 15. Метод переброскиaх2 + bх + c =
- 16. 5х2 – 8х – 4 = 0–
- 17. 2х2 + 5х – 7 = 0–
- 18. 8х2 – 6х + 1 = 08у1
- 19. Скачать презентацию
- 20. Похожие презентации














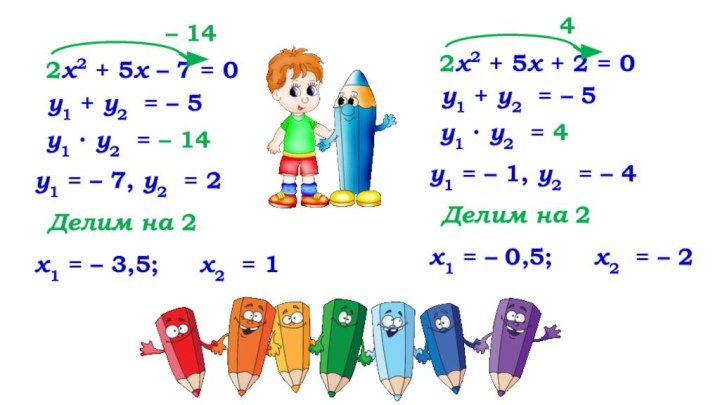


Слайд 5
Устная работа
1). x1 + x2 = – 23 x1
∙ x2 = 132
3). x1 + x2 = –
5 x1 ∙ x2 = – 842). x1 + x2 = 16 x1 ∙ x2 = 63
4). x1 + x2 = – 3 x1 ∙ x2 = – 88
Уравнение имеет отрицательные корни
Уравнение имеет положительные корни
Уравнение имеет корни разных знаков
Уравнение имеет корни разных знаков
Слайд 6
Устная работа
1). х1 + х2 = – 10
х1
∙ х2 = 21
⇒ х1 = – 7,
х2 = – 32). х1 + х2 = – 14
х1 ∙ х2 = 45
⇒ х1 = – 9, х2 = – 5
3). х1 + х2 = 22
х1 ∙ х2 = 120
⇒ х1 = 10, х2 = 12
Слайд 7
Устная работа
4). х1 + х2 = 11
х1
∙ х2 = 10
⇒ х1 = 1, х2
= 105). х1 + х2 = 4
х1 ∙ х2 = – 60
⇒ х1 = – 6, х2 = 10
6). х1 + х2 = – 2
х1 ∙ х2 = –15
⇒ х1 = – 5, х2 = 3
Слайд 8
3х2 – 8х – 15 = 0
1).
1
х1
+
1
х2
=
х1х2
х1
+
х2
aх2 + bх + c = 0
х1
+ х2 =х1х2 =
b
a
c
a
–
х1
х2
=
b
a
–
:
c
a
=
b
a
–
∙
a
c
=
=
b
c
–
=
–8
–15
–
=
8
15
–
Слайд 9
3х2 – 8х – 15 = 0
2).
х12
+
х22
aх2 + bх + c = 0
х1 + х2
=х1х2 =
b
a
c
a
–
=
х12
+
х22
=
+ 2x1x2 – 2x1x2
= (x1 + x2)2 – 2x1x2 =
b
a
–
2
– 2 =
c
a
–8
–15
3
–
– 2 =
3
2
64
9
+
10 =
1
9
17
Слайд 10
3х2 – 8х – 15 = 0
3).
x1
х2
+
x2
х1
=
х1х2
х22
+
х12
aх2 + bх + c = 0
х1
+ х2 =х1х2 =
b
a
c
a
–
х2
х1
=
1
9
17
– 5
=
19
45
–3
Слайд 11
3х2 – 8х – 15 = 0
2).
х13
+
х23
aх2 + bх + c = 0
х1 + х2
=х1х2 =
b
a
c
a
–
=
–
=
(x1 + x2)(x12 – x1x2 + x22) =
8
3
∙
1
9
17
(– 5)
=
26
27
58
Слайд 12
1). х2 – 7х + 12 = 0
х1
+ х2 = 7
х1 ∙ х2 = 12
⇒ х1
= 3, х2 = 4=
(x – 3)(x – 4)
1
(x – 3)
1
+
=
=
(x – 3)(x – 4)
1
x – 4
1 + x – 4
=
(x – 3)(x – 4)
(x – 3)
=
=
x – 4
1
Слайд 13
3). 5х2 + 3х – 2 = 0
a
= 5, b = 3, c = – 2
D = b2 – 4ac
D = 9 + 40 = 49
=
5(x + 1)(x – 0,4)
7
(5x – 2)
5
–
=
=
(x + 1)(5x – 2)
1
x + 1
7
–
(5x – 2)
5
=
=
(x – 4)(5x – 2)
7 – 5x – 5
x1,2 =
– b ± √D
2a
⇒ х1 = –1, х2 = 0,4
=
(x – 4)(5x – 2)
2 – 5x
=
– (5x – 2)
(x – 4)(5x – 2)
=
– 1
x – 4
=
=
1
4 – x
Слайд 14
Решение:
x2 + 6x + q = 0
1). По
тереме Виета
х1 + х2 = – 6
х2 = 2х1
х1
+ 2х1 = – 63х1 = – 6
х1 = – 2
х2 = 2 ∙ (– 2) = – 4
2). По тереме Виета
q = x1 ∙ x2
q = – 2 ∙ (– 4) = 8
Ответ:
х1 = – 2, х2 = – 4, q = 8
Слайд 15
Метод переброски
aх2 + bх + c = 0
∙
а ≠ 0
a2х2 + аbх + аc = 0
(aх)2
+ b(ах) + аc = 0Пусть ах = у
у2 + bу + аc = 0
у1 + у2 = – b
у1 ∙ у2 = ac
x1 = x2 =
у1
у2
a
a
5х2 + 3х – 2 = 0
– 10
у1 + у2 = – 3
у1 ∙ у2 = – 10
у1 = – 5, у2 = 2
Делим на 5
x1 = – 1; x2 = 0,4
Слайд 16
5х2 – 8х – 4 = 0
– 20
у1
+ у2 = 8
у1 ∙ у2 = – 20
у1
= – 2, у2 = 10Делим на 5
x1 = – 0,4; x2 = 2
6х2 – 5х – 1 = 0
– 6
у1 + у2 = 5
у1 ∙ у2 = – 6
у1 = – 1, у2 = 6
Делим на 6
x1 = – 1/6; x2 = 1
Слайд 17
2х2 + 5х – 7 = 0
– 14
у1
+ у2 = – 5
у1 ∙ у2 = –
14у1 = – 7, у2 = 2
Делим на 2
x1 = – 3,5; x2 = 1
2х2 + 5х + 2 = 0
4
у1 + у2 = – 5
у1 ∙ у2 = 4
у1 = – 1, у2 = – 4
Делим на 2
x1 = – 0,5; x2 = – 2
Слайд 18
8х2 – 6х + 1 = 0
8
у1 +
у2 = 6
у1 ∙ у2 = 8
у1 = 2,
у2 = 4Делим на 8
x1 = 0,25; x2 = 0,5
6х2 + 13х + 6 = 0
36
у1 + у2 = – 13
у1 ∙ у2 = 36
у1 = – 9, у2 = – 4
Делим на 6
x1 = – 1,5; x2 = – 2/3