Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

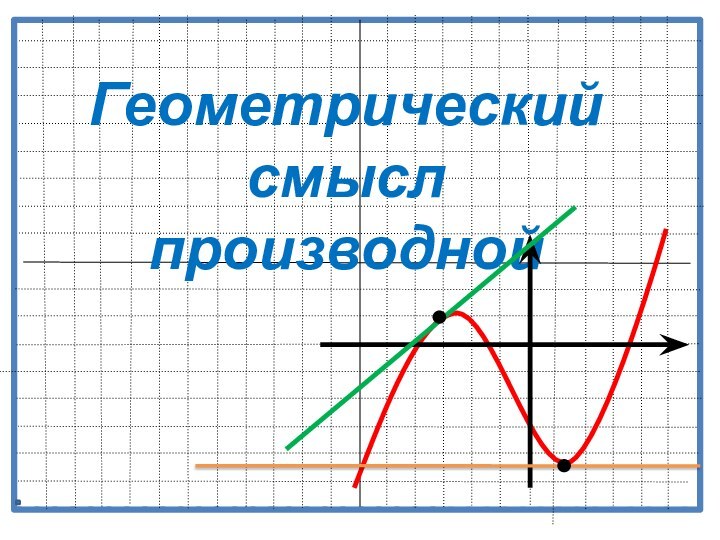
Презентация на тему Геометрический смысл производной функции

Содержание

2. Рано или поздно всякая правильная
3. Цель урока1) выяснить, в чем состоит геометрический
4. Словарь урока производная, линейная функция, угловой коэффициент, непрерывность, тангенсы углов (острый, тупой).
5. Составь пару 3 мин каждый ученик работает
6. Составь пару Ответ.
7. Определение Функция заданная с помощью формулы у=кх+b называется линейной. Число k=tg называется угловым коэффициентом прямой.
8. yx -1 0 1 2y=кх+b
9. yx -1 0 1 2y=кх+b
10. yx 0y=yₒ+к(х-xₒ)x-xₒy-yₒxₒxMₒ(xₒ;yₒ)M(x;y)A(x;yₒ)
11. Уравнение прямой с угловым коэффициентом k, проходящей
12. yx -1 0 1 2Найдите угловой коэффициент прямойy=кх+b
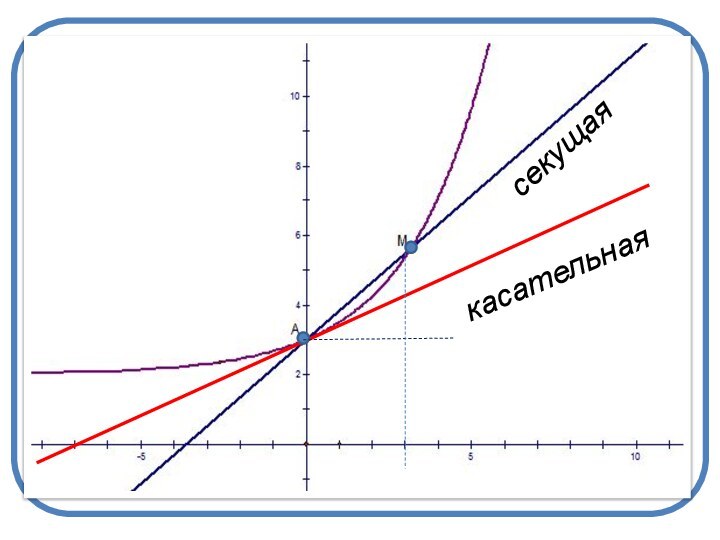
13. ОпределениеКасательной к графику функции у=f(x) называется предельное положение секущей.рисунок
14. касательнаясекущая
15. Практическая исследовательская работа Геометрический смысл
16. Задание1. Постройте касательную к графику функции …
17. Геометрический смысл производной Значение производной функции y=f(х) в
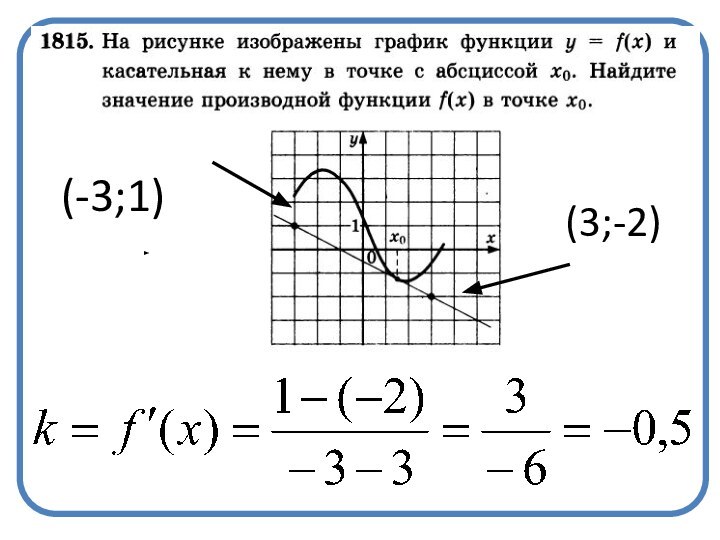
18. (-3;1)(3;-2)
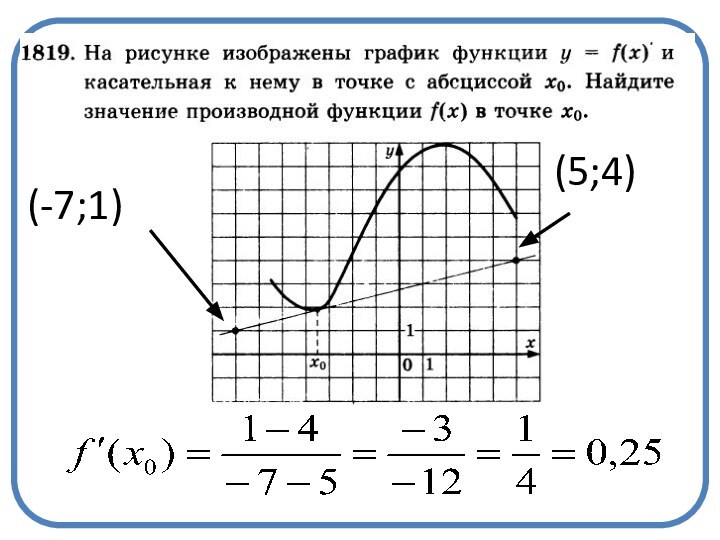
19. (-7;1)(5;4)
20. (-6;3)(0;6)
21. Уравнение касательной к графику функции 1. Запишите
22. Алгоритм составления уравнения касательнойЗапишите уравнение касательной к
23. Задача 1 Напишите уравнение касательной к графику функции
24. Ну кто придумал эту математику !У меня всё получилось!!!Надо решить ещё пару примеров.
25. Спасибо за работу!
26. Скачать презентацию
27. Похожие презентации

Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов

Главная
Алгебра
Геометрический смысл производной функции

Рано или поздно всякая правильная математическая идея находит применение в

Цель урока1) выяснить, в чем состоит геометрический смысл производной, вывести уравнения касательной

Словарь урока производная, линейная функция, угловой коэффициент, непрерывность, тангенсы углов (острый, тупой).

Составь пару 3 мин каждый ученик работает самостоятельно, 2 минуты - работа

Определение Функция заданная с помощью формулы у=кх+b называется линейной. Число k=tg называется угловым коэффициентом прямой.

yx 0y=yₒ+к(х-xₒ)x-xₒy-yₒxₒxMₒ(xₒ;yₒ)M(x;y)A(x;yₒ)

Уравнение прямой с угловым коэффициентом k, проходящей через точку (х0;у0)у=у0+k(x-x0)Уравнение прямой с

yx -1 0 1 2Найдите угловой коэффициент прямойy=кх+b

ОпределениеКасательной к графику функции у=f(x) называется предельное положение секущей.рисунок

Практическая исследовательская работа Геометрический смысл производнойЦель: Используя данные

Задание1. Постройте касательную к графику функции … в точке с абсциссой хₒ=22.

Геометрический смысл производной Значение производной функции y=f(х) в точке х0 равно угловому коэффициенту

Уравнение касательной к графику функции 1. Запишите уравнение прямой с угловым коэффициентом

Алгоритм составления уравнения касательнойЗапишите уравнение касательной к графику функции

Задача 1 Напишите уравнение касательной к графику функции у=f(x) в точке с абсциссой

Ну кто придумал эту математику !У меня всё получилось!!!Надо решить ещё пару примеров.

Литература.1. Алгебра и начала математического анализа 11 класс Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова,

Слайды презентации

Слайд 2

Рано или поздно всякая правильная математическая

идея находит применение в том или ином деле.

А.Н.Крылов

Слайд 3 Цель урока
1) выяснить, в чем состоит геометрический смысл

Цель урока1) выяснить, в чем состоит геометрический смысл производной, вывести уравнения

производной, вывести уравнения касательной к графику функции
2) Развивать ОУУН

мыслительной деятельности: анализ, обобщение и систематизация, логическое мышление, сознательное восприятие учебного материала
3) формировать умение оценивать свой уровень знаний и стремление его повышать, способствовать развитию потребности к самообразованию. Воспитание ответственности, коллективизма.

Слайд 4 Словарь урока
производная, линейная функция, угловой коэффициент, непрерывность,

тангенсы углов (острый, тупой).

Слайд 5 Составь пару
3 мин каждый ученик работает самостоятельно,

Составь пару 3 мин каждый ученик работает самостоятельно, 2 минуты -

2 минуты - работа в парах. Обсуждение результатов и

запись в карточку ответов. (Карточка №1 остается у ученика для самоконтроля, карточка №2 должна быть сдана учителю)

Слайд 6 Составь пару
Ответ.

Слайд 7 Определение
Функция заданная с помощью формулы у=кх+b называется линейной.
Число

k=tg называется угловым коэффициентом прямой.

Слайд 8 y
x
-1 0 1

2
y=кх+b

Слайд 9 y
x
-1 0 1

2
y=кх+b

Слайд 10 y
x
0
y=yₒ+к(х-xₒ)


x-xₒ
y-yₒ
xₒ

x

Mₒ(xₒ;yₒ)
M(x;y)
A(x;yₒ)

Слайд 11 Уравнение прямой с угловым коэффициентом k, проходящей через

Уравнение прямой с угловым коэффициентом k, проходящей через точку (х0;у0)у=у0+k(x-x0)Уравнение прямой

точку (х0;у0)
у=у0+k(x-x0)
Уравнение прямой с угловым коэффициентом k, проходящей через

точку (х0;у0)
у=у0+k(x-x0) (1)

Угловой коэффициент прямой проходящий через точки (х1;у1) и (х0;у0)

(2)

Слайд 12 y
x
-1 0 1

2
Найдите угловой коэффициент прямой
y=кх+b

Слайд 13 Определение
Касательной к графику функции у=f(x) называется предельное положение

секущей.
рисунок

Слайд 14 касательная
секущая

Слайд 15 Практическая исследовательская работа Геометрический смысл производной
Цель:

Практическая исследовательская работа Геометрический смысл производнойЦель: Используя данные практической

Используя данные практической работы определить, в чем состоит геометрический

смысл производной
Оборудование:
Линейки, транспортиры, микрокалькуляторы, миллиметровая бумага с построенным графиком

Слайд 16 Задание
1. Постройте касательную к графику функции … в

Задание1. Постройте касательную к графику функции … в точке с абсциссой

точке с абсциссой хₒ=2
2. Измерьте угол, образованный касательной и

положительным направлением оси оХ.
3. Записать =… .
4. Вычислите с помощью микрокалькулятора
tg =… .
5. Вычислите f´(xₒ ), для этого найдите f´(x)
6. Запишите: f´(x )=…. ; f´(xₒ )=….
7. Выберите две точки на графике касательной, запишите их координаты.
8. Вычислите угловой коэффициент прямой k по формуле

9. Результаты вычисления внесите в таблицу

Слайд 17 Геометрический смысл производной
Значение производной функции y=f(х) в точке

Геометрический смысл производной Значение производной функции y=f(х) в точке х0 равно угловому

х0 равно угловому коэффициенту касательной к графику функции y=f(х)

в точке (х0;f(x0))

Слайд 18 (-3;1)
(3;-2)

Слайд 19 (-7;1)
(5;4)

Слайд 20 (-6;3)
(0;6)

Слайд 21 Уравнение касательной к графику функции
1. Запишите уравнение прямой

Уравнение касательной к графику функции 1. Запишите уравнение прямой с угловым

с угловым коэффициентом k, проходящую через точку

2. Замените k

на , а

у=у0+k(x-x0)

Слайд 22 Алгоритм составления уравнения касательной
Запишите уравнение касательной к графику

функции

в точке с абсциссой в общем виде.
Найдите производную функции .
Вычислите значение производной

4. Вычислите значение функции в точке

5. Подставьте найденные значения в уравнение касательной