не лежащих на одной прямой, и четырёх отрезков, попарно
соединяющих эти точки.Зал №1 Четырёхугольники
Гостинная
Выпуклые
Невыпуклые
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Музей истории четырёхугольников
Содержание
- 2. Четырёхугольник — это геометрическая фигура, состоящая из четырёх
- 3. Зал №1 ЧетырёхугольникиГостинная Приглашаем в путешествие!
- 4. Если никакие стороны четырёхугольника не параллельны, то середина
- 5. Иоганн Карл Фри́дрих Га́усс (нем.
- 6. Вокруг четырехугольника можно описать окружность тогда
- 7. Зал №1 ЧетырёхугольникиКлавдий Птолемей, живший в
- 8. Зал №1 ЧетырёхугольникиЕсли вписанный четырёхугольник имеет
- 9. Зал №1 Четырёхугольники 00 0598 -
- 10. Зал №2 Параллелограмм (др.греч. παραλληλόγραμμον от παράλληλος — параллельный иγραμμή — линия) —
- 11. Зал №2 Параллелограмм В «Началах» Евклида
- 12. Зал №2 ПараллелограммЕвкли́д или Эвкли́д (др.-греч. Εὐκλείδης, ок. 300 г. до н. э.) Древнегреческий
- 13. Четырёхугольник, вершины которого совпадают с серединами
- 14. Зал №2 ПараллелограммУчёныйПьер Вариньон (фр. Pierre
- 15. Зал №3 Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα —
- 16. Зал №2 ТрапецияПосидоний —родился в
- 17. Средняя линия трапеции равна полусумме ее оснований
- 18. Зал №3 ТрапецияГерон Александрийский (Heron,
- 19. Зал №4 РомбТермин «ромб»
- 20. Зал №4 Ромб «Собрание» (συναγωγή).
- 21. Мозаика Пенроуза, плитки Пенроуза -непериодическое
- 22. Зал №5 Прямоугольник Прямоугольник
- 23. Зал №6 Квадрат От латинского quadratum
- 24. Центры квадратов, построенных на сторонах параллелограмма, лежат в
- 25. Теоремы ТебоЗал №6 КвадратЕсли на каждой
- 26. Зал №7 А знаете ли вы?
- 27. Зал №7 А знаете ли вы?2
- 28. Скачать презентацию
- 29. Похожие презентации
Четырёхугольник — это геометрическая фигура, состоящая из четырёх точек, не лежащих на одной прямой, и четырёх отрезков, попарно соединяющих эти точки. Зал №1 ЧетырёхугольникиГостинная Выпуклые
Слайд 2 Четырёхугольник — это геометрическая фигура, состоящая из четырёх точек,
Слайд 4
Если никакие стороны четырёхугольника не параллельны, то середина
отрезка, соединяющего точки пересечения противоположных сторон, лежит на прямой,
соединяющей середины диагоналей.Эта прямая называется прямой Гаусса.
Прямая Гаусса
Зал №1 Четырёхугольники
Слайд 5
Иоганн Карл Фри́дрих Га́усс
(нем.
Johann Carl Friedrich Gauß)
1777,Брауншвейг — 1855, Гёттинген.
Немецкий математик, астроном и физик, величайший математик всех времён,
«король математики».
Учёный
Зал №1 Четырёхугольники
Слайд 6 Вокруг четырехугольника можно описать окружность тогда и
только тогда, когда произведение его диагоналей равно сумме произведений
его противоположных сторон.Зал №1 Четырёхугольники
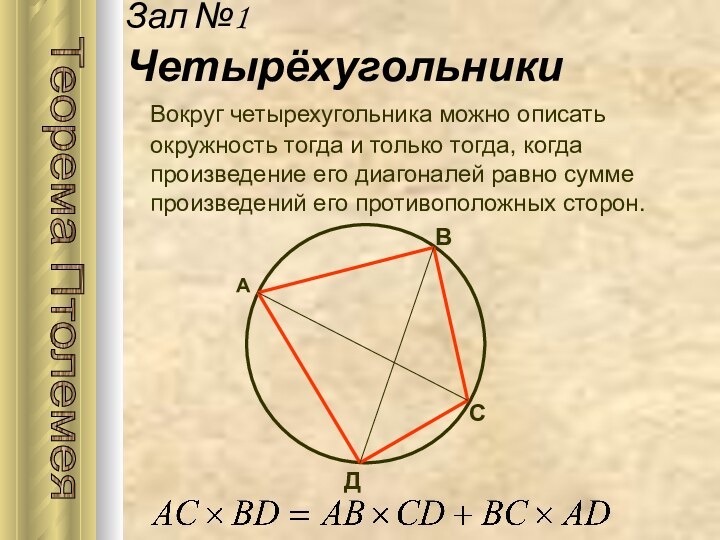
Теорема Птолемея
А
В
С
Д
Слайд 7
Зал №1 Четырёхугольники
Клавдий Птолемей,
живший в конце
первого — начале второго века н.э.
Древнегреческий ученый -
астроном, математик, астролог, географ, оптик и теоретик музыки. . Основной труд Птолемея — “Альмагест”, в котором он изложил сведения по астрономии. Учёный
Слайд 8
Зал №1 Четырёхугольники
Если вписанный четырёхугольник имеет перпендикулярные
диагонали, пересекающиеся в точке M, то прямая, проходящая через точку M и
перпендикулярная одной из его сторон, делит противоположную ей сторону пополам.Теоре́ма Брахмагу́пты
Формула Брахмагупты
Слайд 9
Зал №1 Четырёхугольники
00 0598 - 00
0660
индийский математик
и астроном Брахмагупта
Основные труды:
«Брахма-спхута-сиддханта»
«Кхандакхадьяка»
Учёный
Слайд 10
Зал №2 Параллелограмм
(др.греч. παραλληλόγραμμον от παράλληλος — параллельный иγραμμή — линия) — это четырёхугольник,
у которого противоположные стороны попарно параллельны, то есть лежат
на параллельных прямых. Этимология
Слайд 11
Зал №2 Параллелограмм
В «Началах» Евклида доказывается
следующая теорема:
в параллелограмме противоположные стороны
равны и противоположные углы
равны, а диагональ разделяет его пополам.
из истории
Ватиканский манускрипт
т.1, 38v — 39r. Euclid I prop. 47
Слайд 12
Зал №2 Параллелограмм
Евкли́д или Эвкли́д
(др.-греч. Εὐκλείδης, ок. 300 г. до н. э.)
Древнегреческий математик.
Мировую известность приобрёл благодаря сочинению по основам математики «Начала»
(Στοιχεῖα букв. элементы). Учёный
Слайд 13 Четырёхугольник, вершины которого совпадают с серединами сторон
произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного
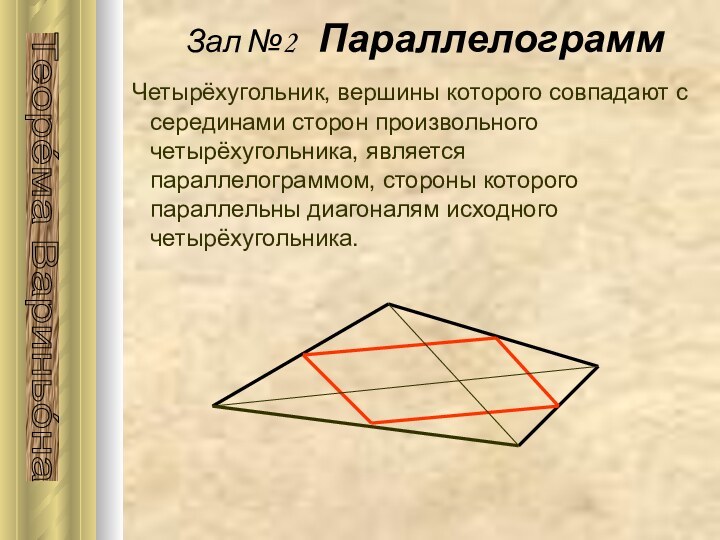
четырёхугольника.Зал №2 Параллелограмм
Теоре́ма Вариньо́на
Слайд 14
Зал №2 Параллелограмм
Учёный
Пьер Вариньон
(фр. Pierre Varignon,
Кан, 1654 —1722, Париж) Французский математик ,
член Парижской
Академии наук, профессор математики коллежа Мазарини профессор Коллеж де Франс.
Основной вклад Вариньон совершил в статику и механику.
Слайд 15
Зал №3 Трапеция
(от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол,
еда») —
четырёхугольник, у которого только одна пара противолежащих сторон параллельна.
«Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония (1в.)
Этимология
Слайд 16
Зал №2 Трапеция
Посидоний —
родился в Апамее
в Сирии в 135 г.,
умер в Риме в
50 г. до Р. Хр. Математик и астроном.
Жил долго в Родосе.
Был учителем Цицерона.
Известен второй попыткой определить размеры земного шара.
Учёный
Слайд 17
Средняя линия трапеции равна полусумме ее оснований
(в трудах Герона Александрийского)
Зал №2
Трапецияиз истории
a
b
m
Слайд 18
Зал №3 Трапеция
Герон Александрийский
(Heron, I
в. н. э.)
Греческий механик и математик.
Занимался геометрией, механикой, гидростатикой, оптикой; изобрел прототип паровой машины и точные нивелировочные инструменты.
Учёный
Слайд 19
Зал №4 Ромб
Термин «ромб» происходит
от др.-греч. ῥόμβος — «бубен».
Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.
Этимология
Слайд 20
Зал №4 Ромб
«Собрание» (συναγωγή).
Автор
Папп Александри́йский
(др.-греч. Πάππος ὁ Ἀλεξανδρεύς) — древнегреческий математик второй половины III века.
Изложено содержание ряда
трудов более древних авторов,добавлены собственные теоремы Паппа. Учёный
Портрет учёного не найден
Слайд 21 Мозаика Пенроуза, плитки Пенроуза -непериодическое разбиение
плоскости, апериодические регулярные структуры, замощение плоскости ромбами двух типов
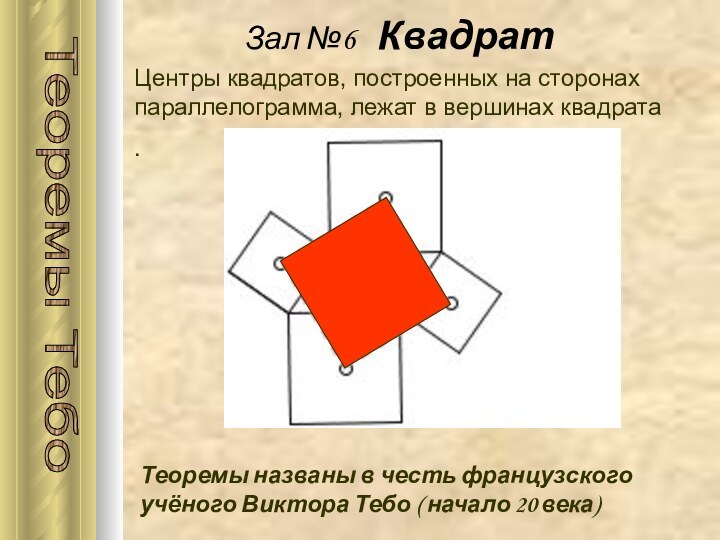
— с углами 72° и 108° и 36° и 144Зал №4 Ромб
интересные факты
Слайд 22
Зал №5 Прямоугольник
Прямоугольник (перевод
с греч. ορθογώνιο.)
Этимология
Первые геометры мыслили прямоугольник вписанным в круг
Слайд 23
Зал №6 Квадрат
От латинского quadratum
(quadrare
- сделать четырехугольным),
перевод с греческого “тетрагонон” - четырехугольник.
Этимология
Слайд 24 Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах
квадрата
.
Зал №6 Квадрат
Теоремы Тебо
Теоремы названы в
честь французского учёного Виктора Тебо ( начало 20 века)
Слайд 25
Теоремы Тебо
Зал №6 Квадрат
Если на каждой из
двух соседних сторон квадрата построить по равностороннему треугольнику (либо
оба внутрь, либо оба вовне квадрата), то вершины этих двух треугольников, не являющиеся вершинами квадрата, и вершина квадрата, не являющаяся вершиной треугольников, образуют равносторонний треугольник.
Слайд 26
Зал №7 А знаете ли вы?
S
- площадь многоугольника с целочисленными вершинами
В -
количество целочисленных точек внутри Г — количество целочисленных точек на границе многоугольника.
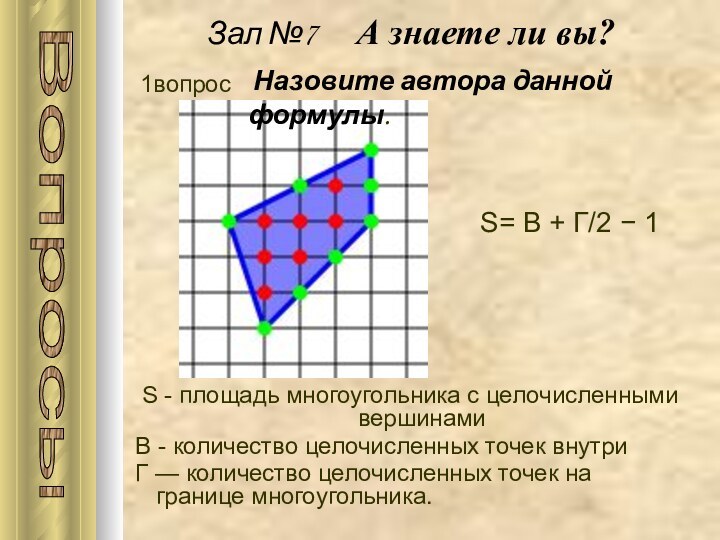
Вопросы
Назовите автора данной формулы.
1вопрос
S= В + Г/2 − 1
Слайд 27
Зал №7 А знаете ли вы?
2 вопрос
Какая фигура называется дельтоидом?
3 вопрос
Какая мышца человека носит
название четырёхугольника?Вопросы
