Презентация на тему Арифметическая и геометрическая прогрессия

б о л а

Т е

о р е м а

К о о р д и н а т а

А л г е б р а

П р я м а я

И н т е р в а л

А к с и о м а

с у м м а

О р д и н а т а

В и е т

материала по данной теме;
отработка умений и навыков применения формул

n –го члена прогрессии, суммы n первых членов прогрессии;
развитие навыков работы с дополнительной литературой, с историческим материалом;
развитие познавательной активности учащихся;
воспитание эстетических качеств и умения общаться; формирование интереса к математике.

Цели урока:

до н.в.) встречаются примеры арифметический прогрессий.
Задачи на прогрессии, дошедшие

до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.
Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым. Ариабхатта (5 в.)применял формулы общего числа, суммы арифметической прогрессии.
Но правило для нахождения суммы членов арифметической прогрессии впервые встречается в сочинении «Книги Абака» в 1202 г.(Леонардо Пизанский).

ИСТОРИЧЕСКАЯ СПРАВКА

со второго равен предыдущему сложенному с одним и тем

же числом.

Последовательность отличных от нуля чисел в которой каждый член начиная со второго равен предыдущему умноженному на одно и тоже число.

Число d - разность прогрессии

Число q - знаменатель прогрессии.

d = a2-a1 = a3-a2 = a4-a3 =….

q = b2:b1 = b3:b2 = b4:b3 =…

d = 5
Найти: a4,.
a4=22
bn=b1qn-1
Дано: b1 = 3, q

= 2

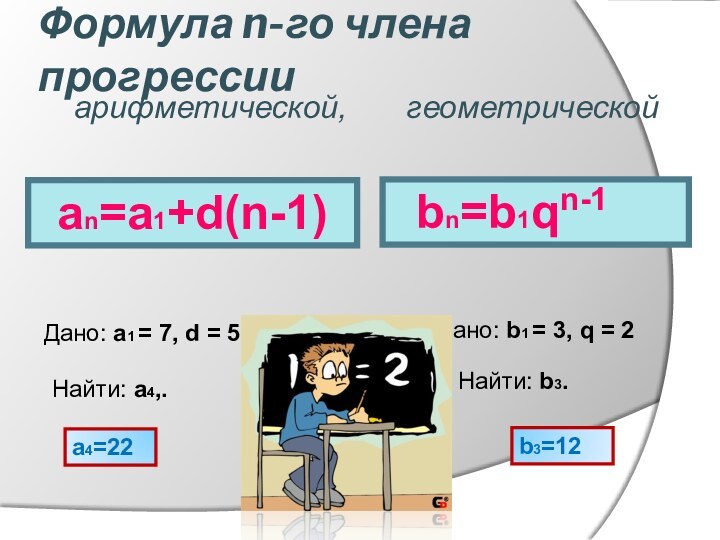
Найти: b3.

b3=12

арифметической,

геометрической

второго есть среднее арифметическое между предыдущим и последующим членами

прогрессии

Каждый член последовательности начиная со второго есть среднее геометрическое между предыдущим и последующим членами последовательности (bn >0)

Характеристическое свойство прогрессий

х1, х2, 4, х4,14, … найти: х4

b1, b2, 1, b4, 16, …- все члены положительные числа найти: b4

Х4=9

b4=4

5, d = 4
Найти: S5
S5 = 65
Дано: b 1

= 2, q = - 3

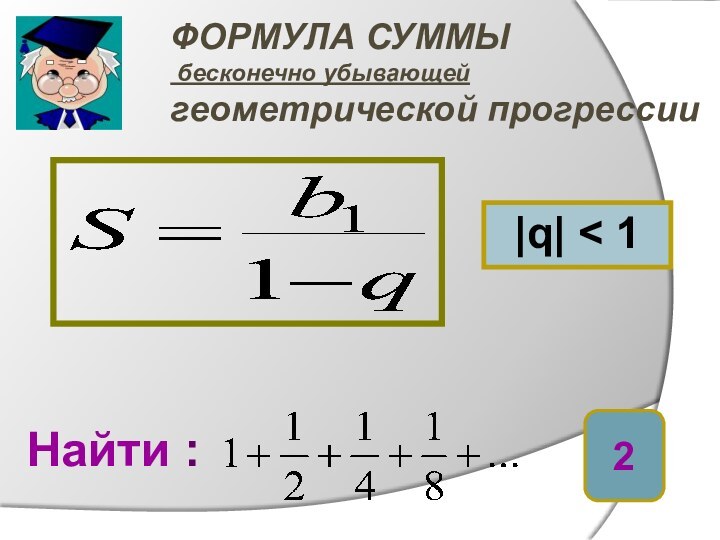
Найти: S4

S4 = - 40

арифметическая

геометрическая

1
Найти :
2

известно, что а7 = 8, а8 = 12. найдите

разность арифметической прогрессии.

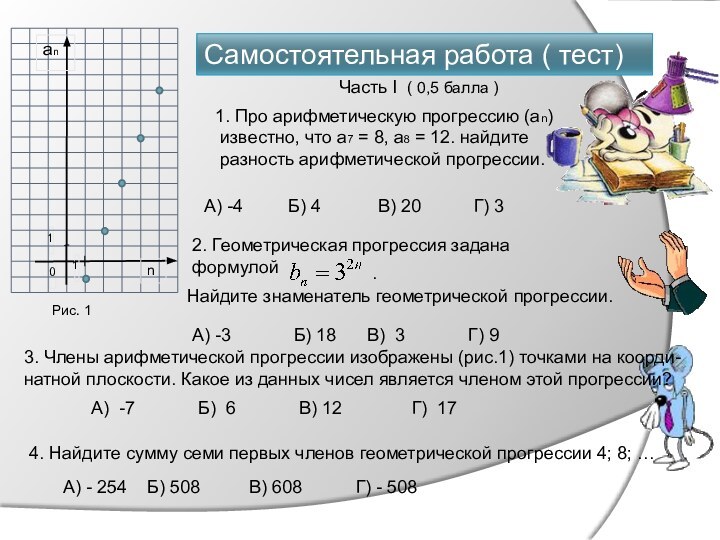
А) -4

Б) 4

В) 20

Г) 3

Б) 18

В) 3

Г) 9

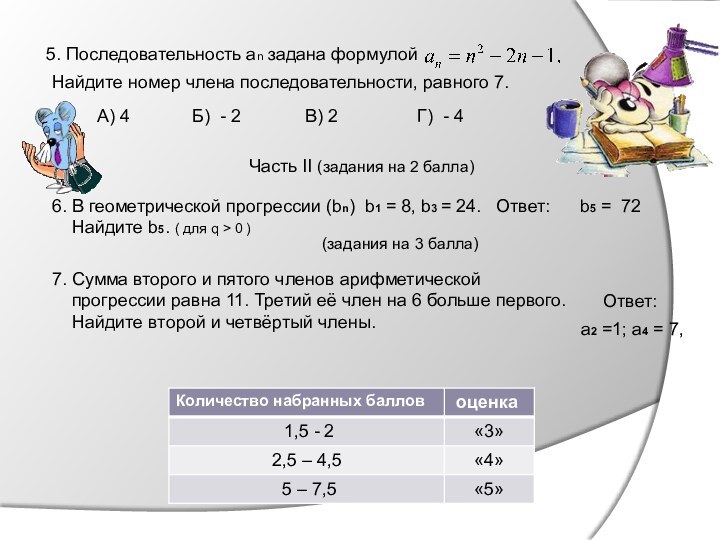
3. Члены арифметической прогрессии изображены (рис.1) точками на коорди- натной плоскости. Какое из данных чисел является членом этой прогрессии?

А) -7

В) 12

Г) 17

4. Найдите сумму семи первых членов геометрической прогрессии 4; 8; …

А) - 254

Б) 508

В) 608

Г) - 508

Часть I ( 0,5 балла )

А) -3

Б) 6

(задания на 2 балла)
6. В геометрической прогрессии (bn) b1

= 8, b3 = 24. Найдите b5. ( для q > 0 )

(задания на 3 балла)

7. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий её член на 6 больше первого. Найдите второй и четвёртый члены.

Критерии оценок:

b5 = 72

Ответ:

Ответ:

а2 =1; а4 = 7,

следующем ряду на 20 мест больше чем в предыдущем,

а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?

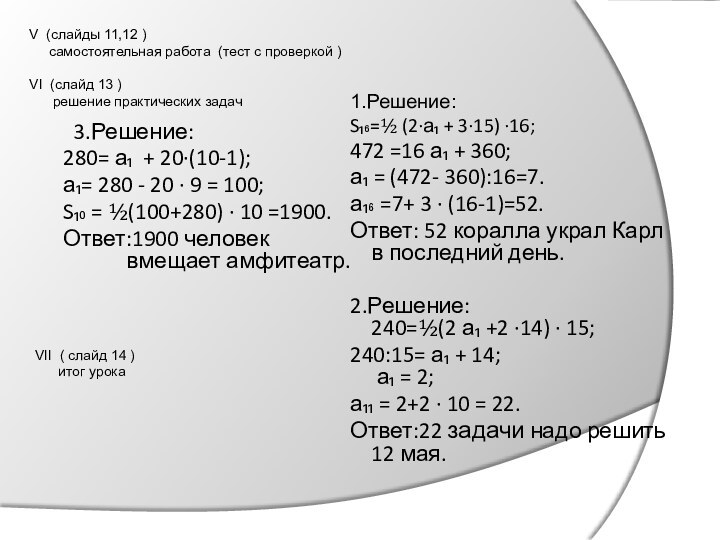
За 16 дней Карл украл у Клары 472 коралла. Каждый день он крал на 3 коралла больше, чем в предыдущий день. Сколько кораллов украл Карл в последний день.
В сборнике по подготовке к экзамену-240 задач. Ученик планирует начать их решение 2 мая, а закончить 16 мая, решая каждый день на две задачи больше, чем в предыдущий день. Сколько задач ученик запланировал решить 12 мая?

Прогрессии в жизни, в быту и не только

который ты
не усвоил ничего нового, ничего не прибавил

к своему образованию.

Ян Амос Коменский

Оцените свои знания и умения на
конец урока. Был ли полезен урок
для каждого из вас? Чем?

сегодняшнего урока мы узнаем, разгадав кроссворд:

1. Как называется

график квадратичной функции?
2. Математическое предложение, справедливость которого доказывается.
3. Упорядоченная пара чисел, задающая положение точки на плоскости.
4. Наука, возникшая в глубокой древности в Вавилоне и Египте, а учащиеся России начинают её изучать с 7 класса.
5. Линия на плоскости, задаваемая уравнением у=кх+b.
6. Числовой промежуток.
7. Предложение, принимаемое без доказательства.
8. Результат сложения
9. Название второй координаты на плоскости.
10. Французский математик 19 века, «отец» алгебры, юрист, разгадал шифр, применяемый испанцами в войне с французами, а нам помог в быстром решении квадратных уравнений.

II (слайд 3) Итак, тема урока «Прогрессии». Прогрессия – латинское слово, означающее "движение вперед", было введено римским автором Боэцием.

- А почему во множественном числе? Какие знаете прогрессии? Давайте сформулируем цели нашего урока.

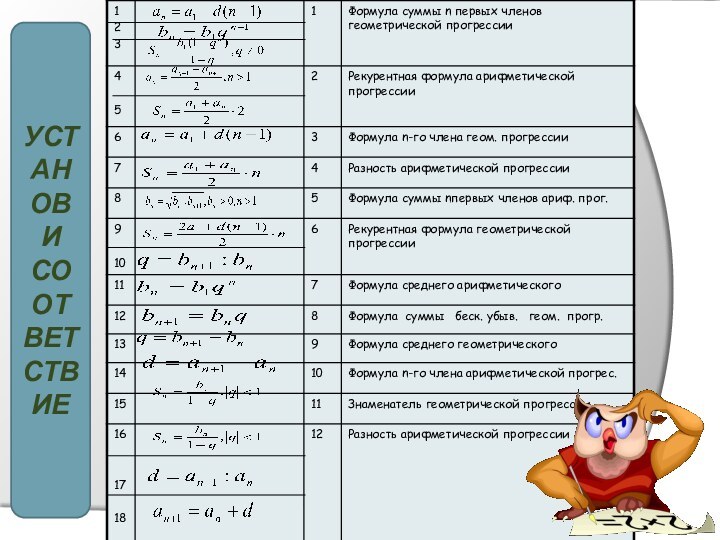
Установи соответствие ответы:
1.- 3 7.- 4
2.- 18 8.- 15
3. - 2 9.- 8
4.- 14 10.- 1
5.- 7 11.- 10
6.- 12 12.-14

III (слайд 4 ) историческая справка ( д/з )
IV ( слайды 5-10 ) обобщение теоретического материала