- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре и началам анализа на тему Площадь криволинейной трапеции и интеграл. Урок-практикум. (11 класс)
Содержание
- 2. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЁ ПЛОЩАДЬ
- 3. Криволинейная трапецияОтрезок [a;b] -основание этой криволинейной трапеции
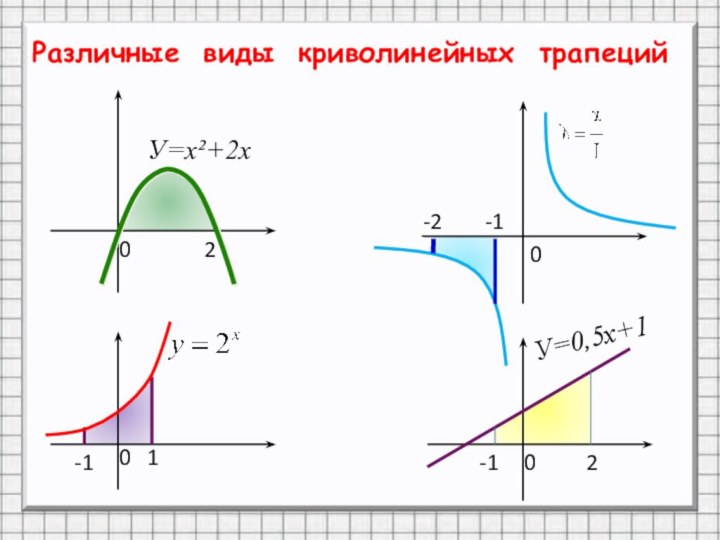
- 4. Различные виды криволинейных трапеций020001-1-12-1-2У=х²+2хУ=0,5х+1
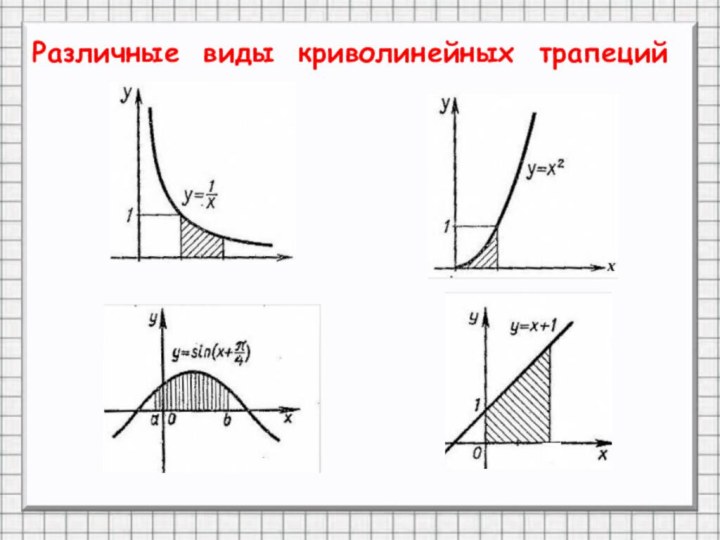
- 5. Различные виды криволинейных трапеций
- 6. ууууууУ=13y = f(x)y = f(x)y = f(x)y
- 7. Самостоятельно решить:Лист 1ЗАДАНИЕ 1.Указать фигуры, которые являются криволинейными трапециями
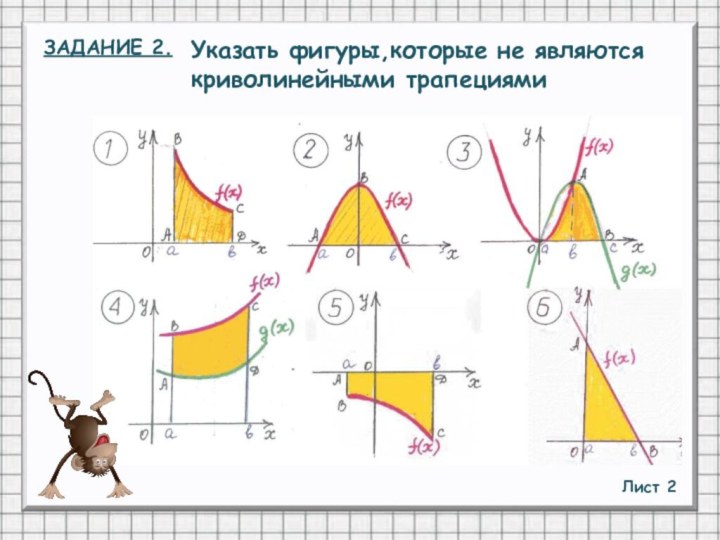
- 8. Лист 2ЗАДАНИЕ 2.Указать фигуры,которые не являются криволинейными трапециями
- 9. F(x) – любая первообразная функции f(x).Не
- 10. Вычислить площадь фигуры, ограниченной линиями у =
- 11. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
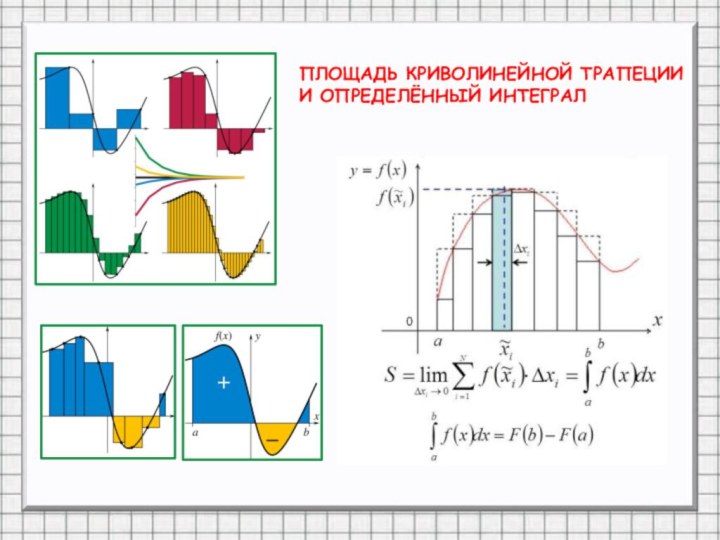
- 12. ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИИ ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
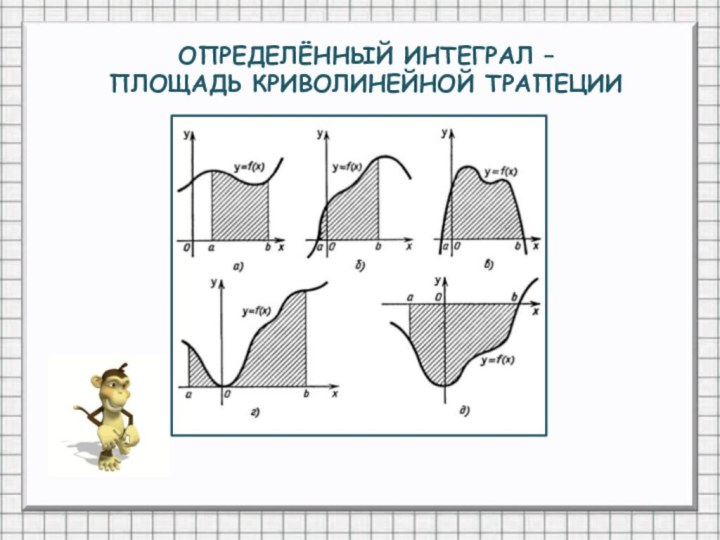
- 13. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ – ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
- 14. Формула Ньютона-Лейбница И.Ньютон1643—1727Г.Лейбниц1646—1716
- 15. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 16. Применение свойств определенного интеграла в вычислениях (образцы)а)б)в)г)д)
- 17. Вычислить интегралы:Вариант 1Вариант 21)1)2)2)3)3)4)4)5)5)6)6)
- 18. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
- 19. С помощью определённого интеграла найти площадькриволинейных трапеций,
- 20. Пример 2. Фигура ограничена линиями
- 21. ТРЕНИНГ «От простого к сложному». По готовым
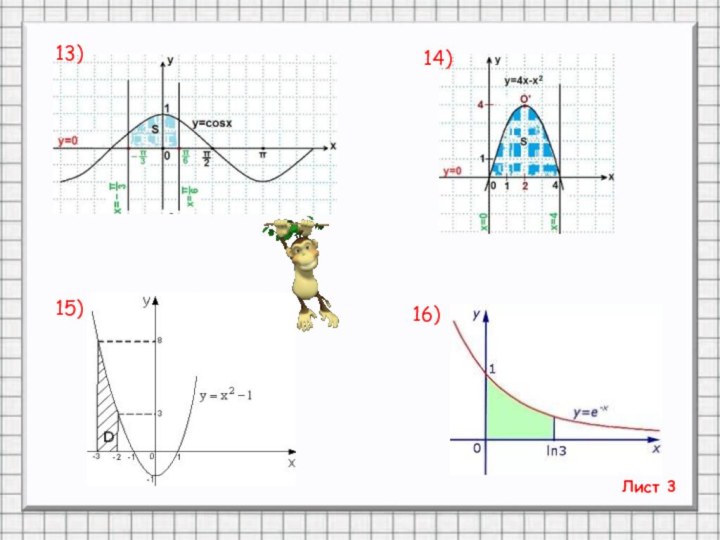
- 22. 7)8)9)10)11)12)Лист 2
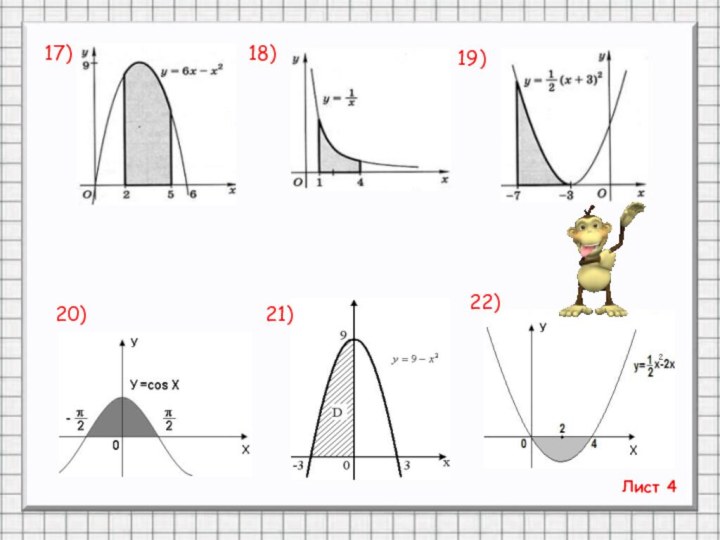
- 23. Лист 313)14)15)16)
- 24. Лист 417)18)19)20)21)22)
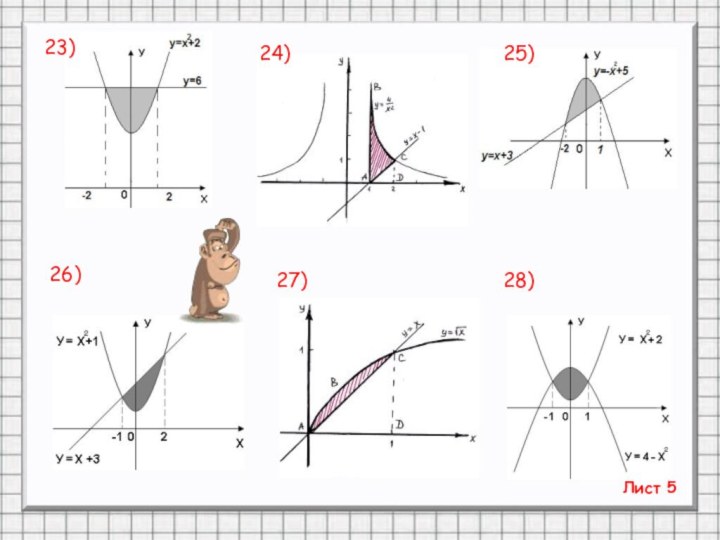
- 25. Лист 523)24)25)26)27)28)
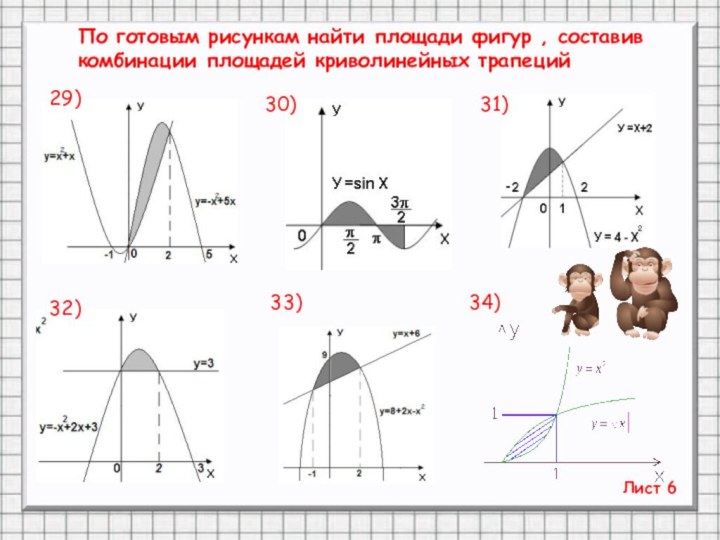
- 26. Лист 630)31)32)33)34)29)По готовым рисункам найти площади фигур , составив комбинации площадей криволинейных трапеций
- 27. Скачать презентацию
- 28. Похожие презентации
КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЁ ПЛОЩАДЬ


![Презентация по алгебре и началам анализа на тему Площадь криволинейной трапеции и интеграл. Урок-практикум. (11 класс) Криволинейная трапецияОтрезок [a;b] -основание этой криволинейной трапеции Опр. Криволинейной трапецией называется фигура,](/img/tmb/6/546081/592b11e2f7297dfe9ce68d0e1c77dc4b-720x.jpg)








Слайд 3
Криволинейная трапеция
Отрезок [a;b] -основание
этой криволинейной трапеции
Опр. Криволинейной трапецией называется фигура,
не меняющей на отрезке [а;b] знак функции f(х), прямыми х=а, x=b и отрезком [а;b].
Слайд 6
у
у
у
у
у
у
У=1
3
y = f(x)
y = f(x)
y = f(x)
y =
f(x)
y = f(x)
y = f(x)
У=3
да
да
да
нет
нет
нет
Являются ли криволинейными трапециями фигуры?
Слайд 7
Самостоятельно решить:
Лист 1
ЗАДАНИЕ 1.
Указать фигуры, которые являются криволинейными
трапециями
Слайд 9
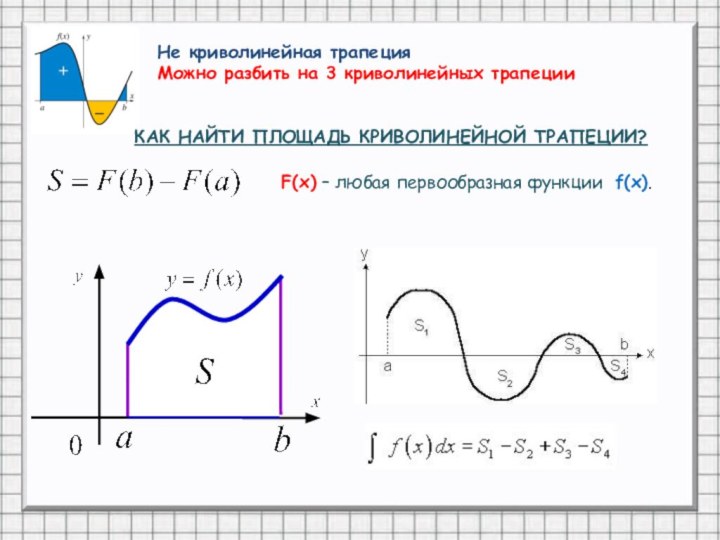
F(x) – любая первообразная функции f(x).
Не криволинейная
трапеция
Можно разбить на 3 криволинейных трапеции
КАК НАЙТИ ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ
ТРАПЕЦИИ?
Слайд 10
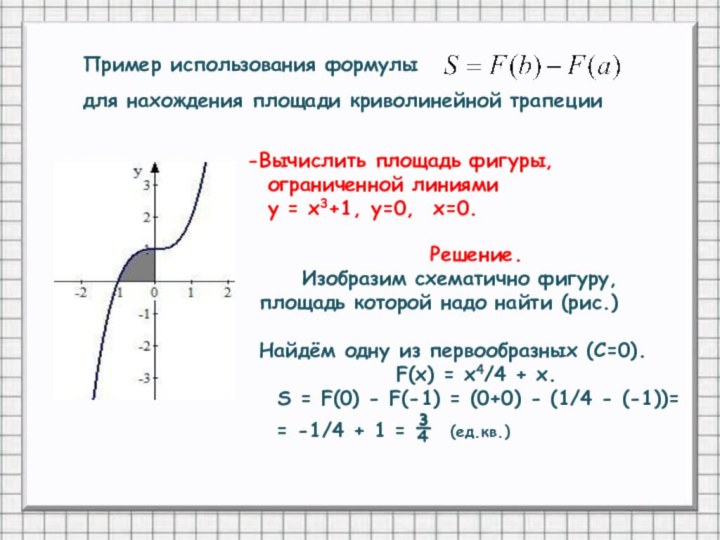
Вычислить площадь фигуры,
ограниченной линиями
у =
x3+1, у=0, x=0.
Решение.
Изобразим схематично фигуру, площадь которой
надо найти (рис.)Найдём одну из первообразных (С=0).
F(x) = x4/4 + x.
S = F(0) - F(-1) = (0+0) - (1/4 - (-1))=
= -1/4 + 1 = ¾ (ед.кв.)
Пример использования формулы
для нахождения площади криволинейной трапеции
Слайд 19
С помощью определённого интеграла найти площадь
криволинейных трапеций, изображенных
на рисунках
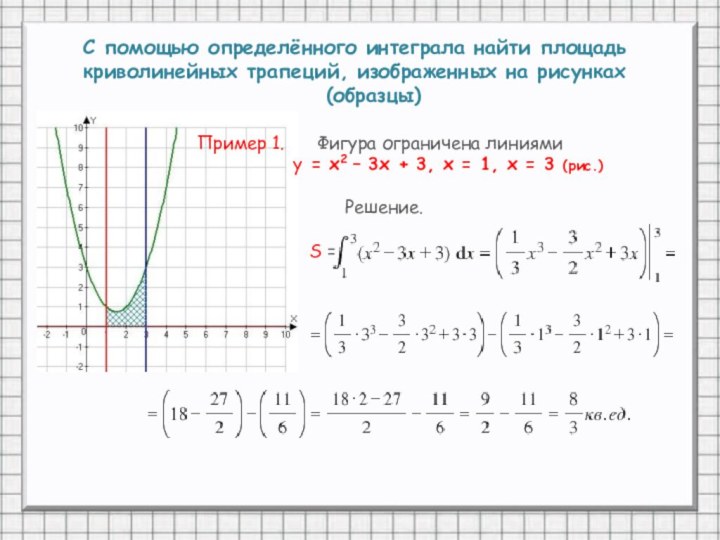
(образцы)Пример 1. Фигура ограничена линиями
у = х2 – 3х + 3, х = 1, х = 3 (рис.)
Решение.
S =
Слайд 20
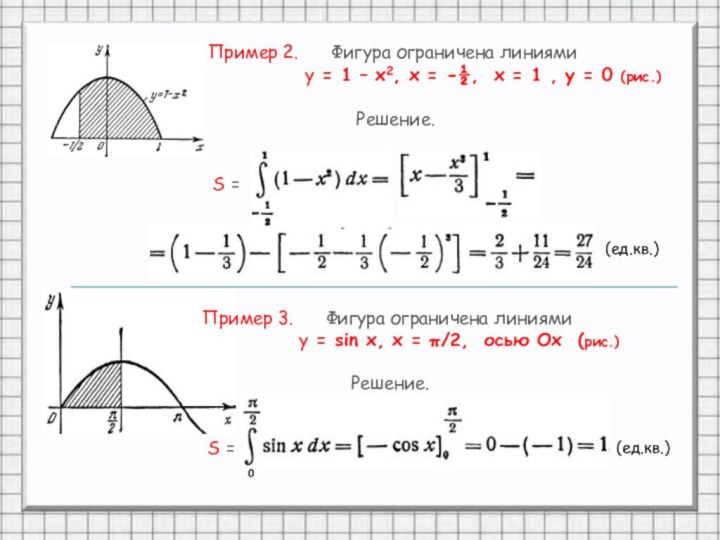
Пример 2. Фигура ограничена линиями
у =
1 – х2, х = -½, х = 1 , у = 0 (рис.)Решение.
S =
(ед.кв.)
Пример 3. Фигура ограничена линиями
у = sin x, x = π/2, осью Ох (рис.)
Решение.
S =
(ед.кв.)
0
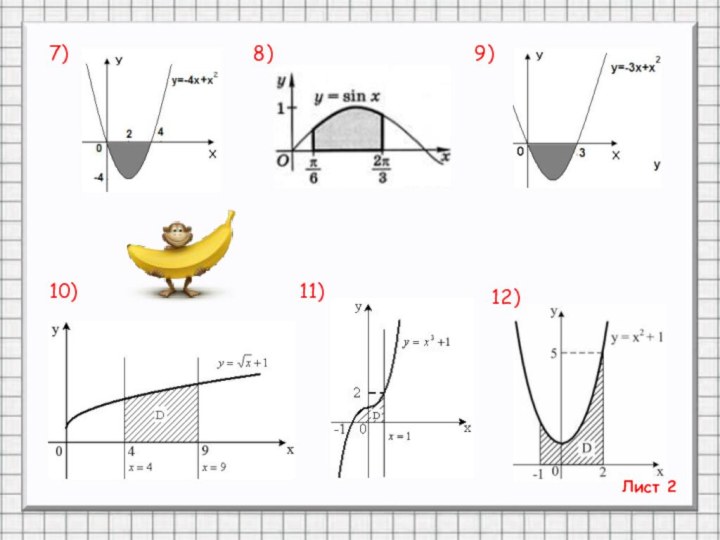
Слайд 21 ТРЕНИНГ «От простого к сложному». По готовым рисункам найти
площади фигур. (Вариант 1 – задания с нечётными номерами, Вариант
2 – с чётными)1)
2)
3)
Лист 1
6)
5)
4)