- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре: Парабола (11 класс)
Содержание
- 2. Парабола — геометрическое место точек, равноудалённых от данной прямой(называемой директрисой параболы) и данной точки (называемой фокусом параболы).Наряду с эллипсом и гиперболой, парабола является коническим сечением.
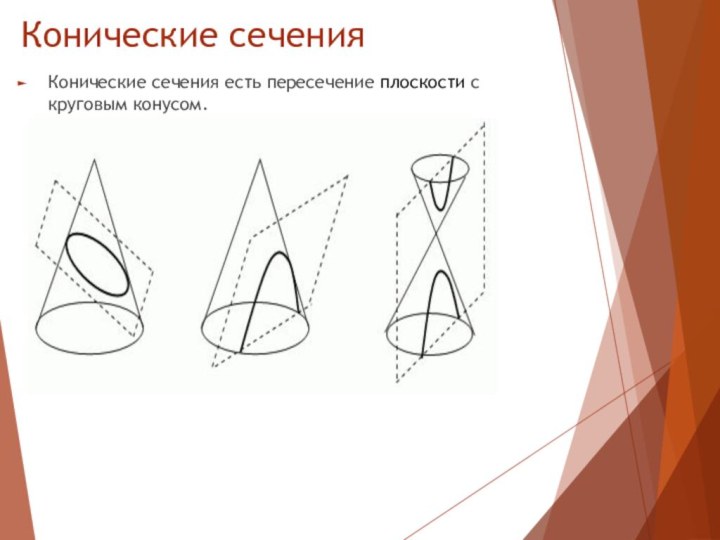
- 3. Конические сеченияКонические сечения есть пересечение плоскости с круговым конусом.
- 4. Пусть на плоскости заданы точка F и прямая
- 5. Директориальное свойство параболы Для произвольной точки M
- 6. Каноническое ур-е параболыПусть расстояние между фокусом и
- 7. Вывод уравнения параболыВ выбранной системе координат фокусом
- 8. Дополнительный материалИсторическая справкаОткрывателем конических сечений предположительно считается
- 9. Парабола у ЛобачевскогоГрафик движения иона по параболе
- 10. Парабола в жизни
- 11. Скачать презентацию
- 12. Похожие презентации
Парабола — геометрическое место точек, равноудалённых от данной прямой(называемой директрисой параболы) и данной точки (называемой фокусом параболы).Наряду с эллипсом и гиперболой, парабола является коническим сечением.










Слайд 2
Парабола — геометрическое место точек, равноудалённых от данной прямой(называемой
директрисой параболы) и данной точки (называемой
фокусом параболы).
Наряду
с эллипсом и гиперболой, парабола является коническим сечением.
Слайд 4 Пусть на плоскости заданы точка F и прямая
, не проходящая через F. Парабола - множество всех тех
точек M плоскости, каждая из которых равноудалена от точки F и прямой . Точка F называется фокусом, прямая - директрисой параболы; (OF) - ось, O - вершина, - фокальный радиус. Эксцентриситет:
Фокальный радиус:
Уравнение директрисы:
Уравнение касательной
в точке M(x0,y0):
Слайд 5
Директориальное свойство параболы
Для произвольной точки M параболы отношение
расстояния до фокуса F к расстоянию до директрисы d
равно единице. e=1
Слайд 6
Каноническое ур-е параболы
Пусть расстояние между фокусом и директрисой
параболы равно p. Тогда в выбранной системе координат парабола
имеет уравнениеp
Слайд 7
Вывод уравнения параболы
В выбранной системе координат фокусом параболы
служит точка , а
директриса имеет уравнение . Пусть текущая точка параболы. Тогда по формуле для плоского случая находимРасстоянием от точки M до директрисы l служит длина перпендикуляра MK, опущенного на директрису из точки M. Из рисунка очевидно, что
Тогда по определению параболы MK=FM ,то есть:
Приводя подобные члены, получаем каноническое уравнение параболы





























