Презентация на тему по математике на тему Задачи на работу

125% работы – это 1,25 части.
Выполнили в 2

раза больший объем работы – это 2 части.

Осталось выполнить еще 5% работы. Это, значит, выполнено 95% работы, т.е. 0,95 части.

В задачах выполненную работу мы обозначили, как 1 часть.

Другие случаи. Дроби, проценты…

Выполнено 80% работы – это 0,8 части.

Работа может измеряться и в других единицах измерения.

в задаче о наполнении объемов работа будет измеряться в м3;
в задаче о погрузке работа может быть в ящиках, мешках;
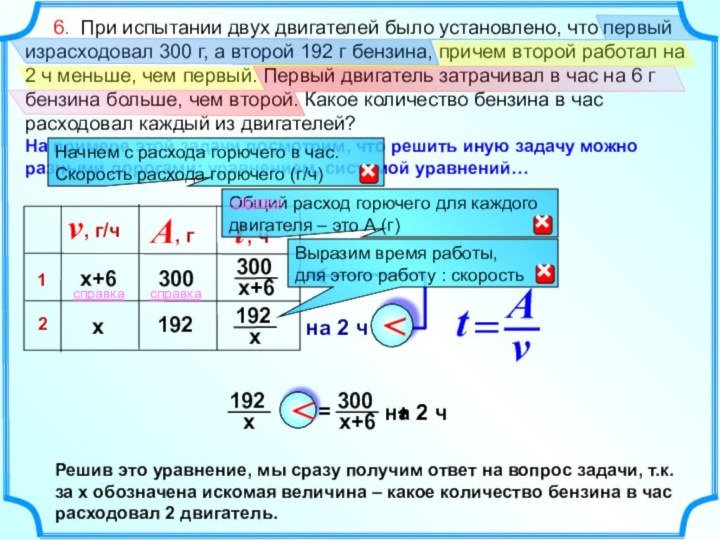
задачи о рабочих, изготовляющих детали, работа в дет.;
для каменщика – в кирпичах, для швеи – в платьях и т.д.

по плану изготовить за несколько дней 216м3 древесины. Первые

три дня бригада выполняла ежедневно установленную планом норму, а затем каждый день заготовляла на 8м3 сверх плана. Поэтому за день до срока было заготовлено 232м3 древесины. Сколько м3 древесины должна была бригада заготовлять по плану?

3

232-3х

3

х+8

х

справка

справка

справка

справка

х

справка

+ 3

<

на 1 день

+ 1

=

Реши уравнение самостоятельно

изготовляет на 5 деталей больше, чем второй. Если первый

будет каждый день изготовлять на одну деталь, а второй на 9 деталей больше, чем они изготовляют, то за 6 дней первый изготовит столько деталей, сколько обрабатывает второй за полных дней. Сколько деталей изготовляет каждый рабочий в день?

х+5

х

х+6

х+9

6

a

( )

( )

Это условие поможет ввести х …

+ 1=

a

6

a

х+9

х+6

справка

Ответ: 1й рабочий изготовлял 14 дет./день, 2й рабочий – 9 дет./день.

справка

величины, которые требуется найти по условию задачи, либо те,

которые необходимы для отыскания искомых величин;

Решение задачи с помощью системы уравнений обычно проводят в такой последовательности:

3. Решают составленную систему уравнений и из полученных решений отбирают те, которые подходят по смыслу задачи.

2. Используя введенные переменные, а также указанные в условии задачи конкретные значения переменных и соотношения между ними, составляют систему уравнений, т.е. «переводят» текст задачи на язык алгебры, составляя систему равенств алгебраических выражений.

в день 100 деталей. Во второй день мастер изготовил

на 20% больше, а ученик – на 10% больше, чем в первый день. Всего во второй день мастер и ученик изготовили 116 деталей. Сколько деталей изготовил мастер и сколько изготовил ученик в первый день?

1,1у

1,2х

х + у = 100

справка

справка

Реши систему уравнений самостоятельно

4. Двое рабочих, работая вместе, выполнили работу за 2

дня. Сколько времени нужно каждому из них на выполнение всей работы, если известно, что если бы первый проработал 2 дня, а второй один, то

всего было бы сделано всей работы.

справка

справка

= 1

справка

справка

t =

2

2

справка

справка

1

у

A1=

A2 =

1

2

+

рабочим было поручено изготовить партию одинаковых деталей. После того

как первый проработал 7 ч и второй 4 ч, оказалось,

что они выполнили всей работы. Проработав совместно еще 4 ч, они

установили, что им остается выполнить всей работы. За сколько

часов каждый из рабочих, работая отдельно, мог бы выполнить всю работу?

Вопрос задачи поможет нам ввести х и у

справка

4

у

7

справка

справка

4 =

–

+

справка

18ч мог бы выполнить всю работу 1й рабочий, работая

отдельно, за 24 ч – 2й рабочий.

было установлено, что первый израсходовал 300 г, а второй

192 г бензина, причем второй работал на 2 ч меньше, чем первый. Первый двигатель затрачивал в час на 6 г бензина больше, чем второй. Какое количество бензина в час расходовал каждый из двигателей?

На примере этой задачи посмотрим, что решить иную задачу можно разными дорогами: уравнением, системой уравнений…

х+6

300

х

<

на 2 ч

+ 2

=

192

справка

справка

справка

Решив это уравнение, мы сразу получим ответ на вопрос задачи, т.к. за х обозначена искомая величина – какое количество бензина в час расходовал 2 двигатель.

было установлено, что первый израсходовал 300 г, а второй

192 г бензина, причем второй работал на 2 ч меньше, чем первый. Первый двигатель затрачивал в час на 6 г бензина больше, чем второй. Какое количество бензина в час расходовал каждый из двигателей?

Составить уравнение можно иначе…

х+2

300

х

>

на 6 г/ч

+ 6

=

192

справка

справка

справка

Но, решив это уравнение, придется сделать еще дополнительные действия, чтобы ответить на вопрос задачи.

было установлено, что первый израсходовал 300 г, а второй

192 г бензина, причем второй работал на 2 ч меньше, чем первый. Первый двигатель затрачивал в час на 6 г бензина больше, чем второй. Какое количество бензина в час расходовал каждый из двигателей?

Решим эту же задачу с помощью системы уравнений…

х+2

y+6

х

y

справка

справка

справка

(х+2)(у+6)

ху

= 300

= 192

192
3х2 – 48х + 192 = 0
Теперь ответим на

вопрос задачи.

24 г/ч расходует 2й двигатель,

30 г/ч – 1й двигатель.

пешки для определенного числа комплектов шахмат. Он хочет научиться

изготовлять ежедневно на 2 пешки больше, чем теперь; тогда такое же задание он выполнит на 10 дней быстрее. Если бы ему удалось научиться изготовлять на 4 пешки больше, чем теперь, то срок выполнения такого же задания уменьшился бы на 16 дней. Сколько комплектов шахмат обеспечит пешками этот ученик, если для каждого комплекта нужно 16 пешек?

x+2

x+4

Составьте и решите систему уравнений самостоятельно.

Найдите ответ на вопрос задачи.

станках. Производительность первого станка на 40% больше производительности второго.

Сколько деталей было обработано за смену каждым станком, если первый работал в эту смену 6 ч, а второй – 7 ч, причем вместе они обработали 616 деталей?

2.

Двое рабочих вместе могут выполнить некоторую работу за 10 дней. После семи дней совместной работы один из них был переведен на другой участок, а второй закончил работу, проработав еще 9 дней. За сколько дней каждый рабочий мог выполнить всю работу?

3.

Две бригады колхозников должны закончить уборку урожая за 12 дней. После 8 дней совместной работы первая бригада получила другое задание, поэтому вторая закончила оставшуюся часть работы за 7 дней. За сколько дней могла бы убрать урожай каждая бригада, работая отдельно?