Презентация на тему исследовательской работы по математике на тему Графический способ решения уравнений с параметрм

мысли, что математика имеет широкую возможность к исследованию окружающей

действительности. Так, как она сама взята из этого мира и выражает часть присущих ему форм и связей. Существует много задач в физике, биологии, экономике, экологии и т.д. для решения которых возникает необходимость построения математических моделей процессов, содержащих две меняющиеся величины: переменную и параметр. Этой моделью является уравнение с параметром. Некоторые из таких уравнений легче всего решаются графически. Этот подход нагляден и более доступен для понимания учащихся. При решении задач с параметром четче осознаешь суть изучаемых явлений
Цель проекта исследования. При помощи построения графиков функций и элементов математического анализа научится решать уравнения с параметром и применять эти знания в перспективе к решению прикладных задач описывающих проблемы из экономики, экологии, политики, смежной науки- физики и т.д..
В данный момент лично для меня и учащихся старших классов наибольшую ценность имеет умение решать задачи с параметром, которые предлагаются на ЕГЭ.
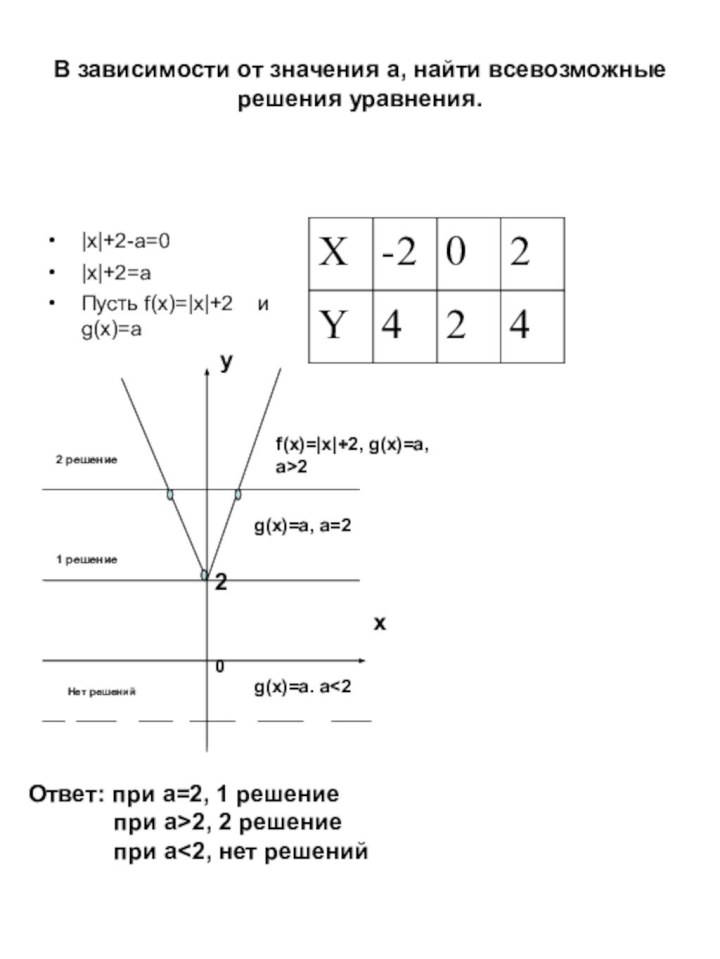
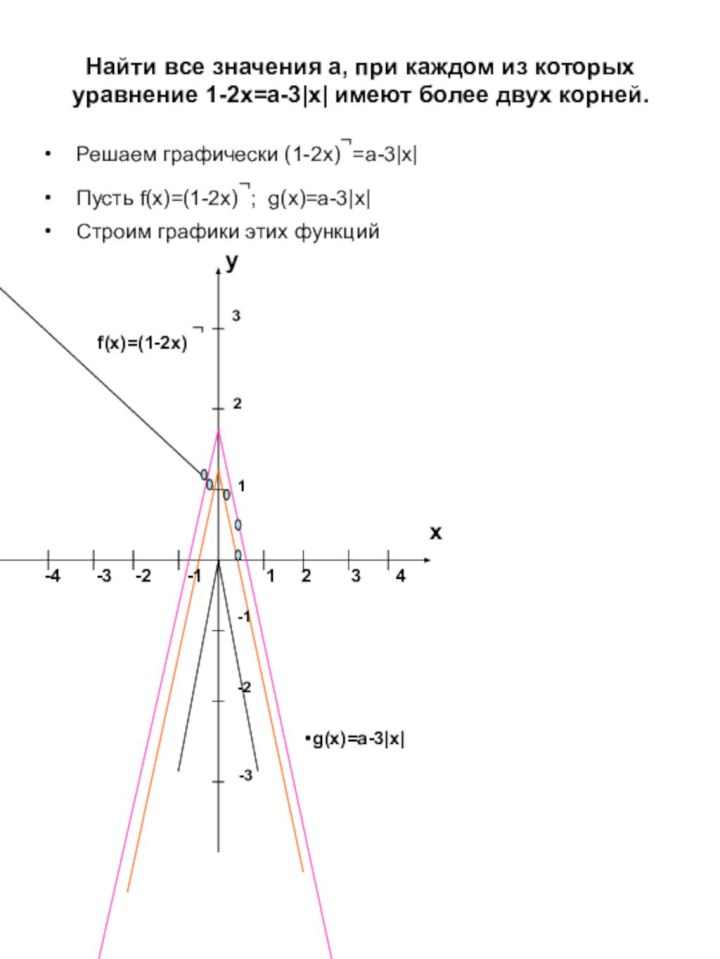
Коротко о сути графического способа решения уравнения с параметром. Записывают уравнение так, чтобы слева от «равно» стояла функция без параметра, а справа от «равно» находилась функция с параметром. Строят графики этих функций. Решением уравнения является общая точка этих функций то, есть абсцисса точки пересечения графиков. Задачей является, найти все значения параметра «а» при которых графики функций пересекаются в нужном количестве точек. Приведу решение трех не очень сложных уравнений.

уравнения.
|x|+2-a=0
|x|+2=a
Пусть f(x)=|x|+2 и g(x)=a




2 решение
1 решение
Нет решений
g(x)=a.

a<2

g(x)=a, a=2

f(x)=|x|+2, g(x)=a, a>2

y

x

2

Ответ: при а=2, 1 решение
при а>2, 2 решение
при a<2, нет решений

0

уравнения.
x2-2x-a=0
x(x-2)=a
Пусть f(x)=x(x-2) и g(x)=a
Построим графики, где
xв=1
Ув=-1

для параболы

у

3

2 решения

g(x), a>1

1 решение

Нет решения

g(x)=a, a=1

g(x)=a, a<1

x

-1

3

0

1

Ответ: при а=1, 1 решение
при a>1, 2 решения
при a<1, нет решений

уравнение 1-2х=а-3|x| имеют более двух корней.
Решаем графически (1-2х)¬=а-3|x|
Пусть

f(x)=(1-2x)¬; g(x)=a-3|x|
Строим графики этих функций

у

х

f(x)=(1-2x) ¬

-4

-3

-2

-1

1

2

3

4

1

2

3

-1

-2

-3

g(x)=a-3|x|