Презентация на тему Физический и геометрический смысл производной

Содержание

2. Производной функции называется предел отношения приращения функции
3. Нахождение производной называется дифференцированием. Вводится определение дифференцируемой
4. Физический смысл производной x`(t) от непрерывной функции
5. - Представьте, что вы летите в самолёте
6. Рассмотрим график функции y = f (
7. Ньютон — создатель первой научной «механической картины
8. Движение, в широком смысле этого слова, охватывает
9. Дифференцирование — уникальный математический метод, применяемый не
10. Скачать презентацию
11. Похожие презентации

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:Производная функции

Главная
Алгебра
Физический и геометрический смысл производной

Выполненоученицей 10 класса «А»ГБОУ СОШ № 323Викторией Петровой Физический и геометрический смысл производной функции

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение

Нахождение производной называется дифференцированием. Вводится определение дифференцируемой функции: Функция f, имеющая производную

Физический смысл производной x`(t) от непрерывной функции x(t) в точке t (0)

- Представьте, что вы летите в самолёте и у вас на руке

Рассмотрим график функции y = f ( x ): Из рис.1 видно,

Ньютон — создатель первой научной «механической картины мира», в которой «земные» и

Движение, в широком смысле этого слова, охватывает все происходящие во вселенной изменения

Дифференцирование — уникальный математический метод, применяемый не только в математике, но и

Слайды презентации

Слайд 2 Производной функции называется предел отношения приращения функции к

Производной функции называется предел отношения приращения функции к приращению аргумента, когда

приращению аргумента, когда приращение аргумента стремится к нулю:

Производная функции

Слайд 3 Нахождение производной называется дифференцированием. Вводится определение дифференцируемой функции:

Нахождение производной называется дифференцированием. Вводится определение дифференцируемой функции: Функция f, имеющая

Функция f, имеющая производную в каждой точке некоторого промежутка,

называется дифференцируемой на данном промежутке.

Дифференцирование

Слайд 4 Физический смысл производной x`(t) от непрерывной функции x(t)

Физический смысл производной x`(t) от непрерывной функции x(t) в точке t

в точке t (0) – есть мгновенная скорость изменения

величины функции, при условии, что изменение аргумента Δt стремится к нулю.

Физический смысл производной функции

Слайд 5 - Представьте, что вы летите в самолёте и

- Представьте, что вы летите в самолёте и у вас на

у вас на руке часы. Когда Вы летите, Вы

имеете скорость равную скорости самолёта.

- А какая скорость у Вас и у самолёта в каждый момент времени на Ваших часах?

– Скорость, как физическое понятие, это путь самолёта, пройденный за единицу времени (например, за час (км/час)), а у Вас, когда Вы взглянули на часы прошло только мгновение. Таким образом, мгновенная скорость (величина пути, пройденного за мгновение) и есть производная величина от функции, описывающей путь самолёта по времени. Мгновенная скорость - это и есть физический смысл производной.

Еще одно объяснение физического смысла производной функции

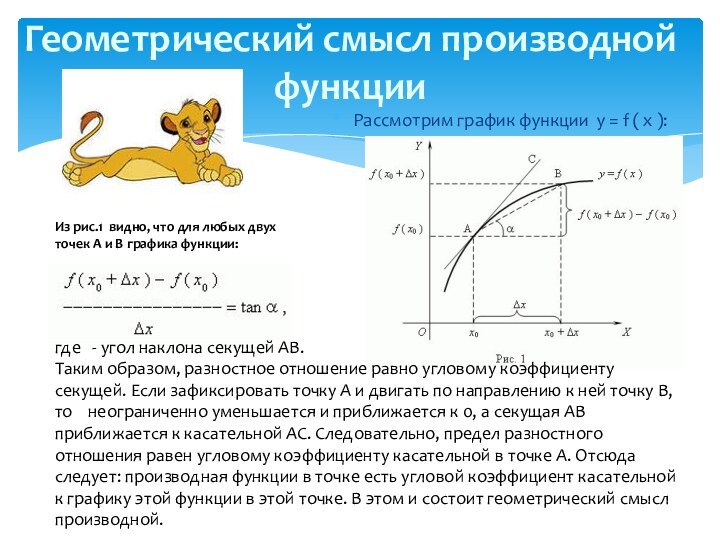
Слайд 6 Рассмотрим график функции y = f ( x

Рассмотрим график функции y = f ( x ): Из рис.1

):

Из рис.1 видно, что для любых двух точек

A и B графика функции:

где - угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Геометрический смысл производной функции