Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Свойства числовых неравенств 8 класс

Содержание

Свойства числовых неравенств. Ребята, с неравенствами мы уже сталкивались, например, когда только начинали знакомиться с понятием корня квадратного. Интуитивно понятно, что с помощью неравенств можно оценить какое из данных чисел больше или меньше. Для математического описания достаточно
Занимательная математикаАлгебра 8 класс.Урок на тему:Свойства числовых неравенств Свойства числовых неравенств. Ребята, с неравенствами мы уже сталкивались, например, когда только начинали Свойства числовых неравенств. Свойство 1. Если a>b и b>c то a>c. Доказательство. Вроде бы Свойства числовых неравенств. Свойство 2. Если a>b, то a+c>b+c. Иначе говоря, если число Свойства числовых неравенств. Свойство 4. Если a>b и c>d, то a+c>b+d. Доказательство. Из условия Свойства числовых неравенств. Свойство 6. Если a>b (a>0, b>0), то Свойства числовых неравенств. Свойство 8. Если a>0, то тогда выполняется неравенство Доказательство. Рассмотрим разность Свойство Свойства числовых неравенств. Пример 1. Известно что -1.5 Свойства числовых неравенств. г) Сначала умножим все части неравенства 3.1 Свойства числовых неравенств. Пример 2. Сравните числа а) б) Решение. а) Возведем каждое Свойства числовых неравенств. Задачи для самостоятельного решения. 1. Известно что -2.2
Слайды презентации

Слайд 2 Свойства числовых неравенств.
Ребята, с неравенствами мы уже сталкивались,

Свойства числовых неравенств. Ребята, с неравенствами мы уже сталкивались, например, когда только

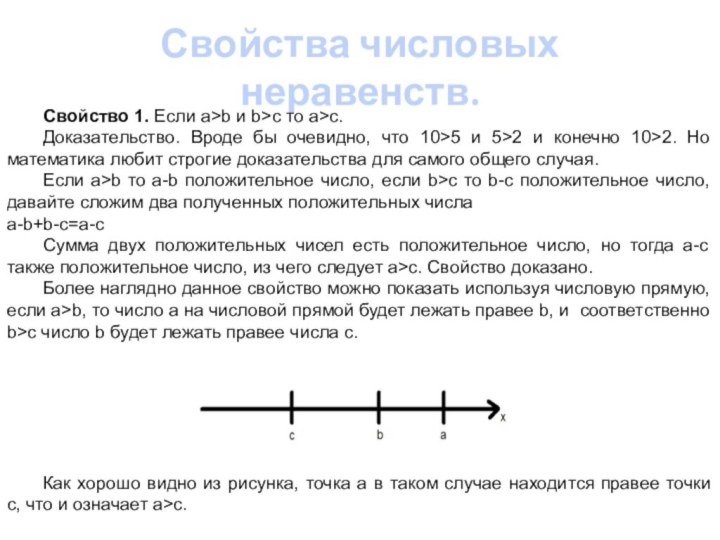
например, когда только начинали знакомиться с понятием корня квадратного.

Интуитивно понятно, что с помощью неравенств можно оценить какое из данных чисел больше или меньше. Для математического описания достаточно добавить специальный символ, который будет означать либо больше, либо меньше.

Запись на математическом языка a>b означает, что число a больше числа b, что в свою очередь значит a-b положительное число.

Запись на математическом языка a
Как и практически все математические объекты неравенства имеют некоторые свойства, изучением таких свойств мы и займемся на этом уроке.



Слайд 3 Свойства числовых неравенств.
Свойство 1. Если a>b и b>c

Свойства числовых неравенств. Свойство 1. Если a>b и b>c то a>c. Доказательство. Вроде

то a>c.
Доказательство. Вроде бы очевидно, что 10>5 и 5>2

и конечно 10>2. Но математика любит строгие доказательства для самого общего случая.
Если a>b то a-b положительное число, если b>c то b-c положительное число, давайте сложим два полученных положительных числа
a-b+b-c=a-c
Сумма двух положительных чисел есть положительное число, но тогда a-c также положительное число, из чего следует a>c. Свойство доказано.
Более наглядно данное свойство можно показать используя числовую прямую, если a>b, то число a на числовой прямой будет лежать правее b, и соответственно b>c число b будет лежать правее числа с.






Как хорошо видно из рисунка, точка a в таком случае находится правее точки c, что и означает a>c.



Слайд 4 Свойства числовых неравенств.
Свойство 2. Если a>b, то a+c>b+c.

Свойства числовых неравенств. Свойство 2. Если a>b, то a+c>b+c. Иначе говоря, если

Иначе говоря, если число a больше числа b, то

какое бы мы число не прибавили (положительное или отрицательное) к этим числам, то знак неравенства будет так же сохраняться. Доказывается данное свойство очень легко, нужно так же выполнить вычитание и та переменная, которую прибавляли, исчезнет, и получится верное исходное неравенство.

Свойство 3.
а) Если обе части неравенства умножить на положительное число, то знак неравенства сохраняется.
Если a>b и c>0, тогда ac>bc.
б) Если обе части неравенства умножить на отрицательное число, то знак неравенства следует поменять на противоположный.
Если a>b и c<0, тогда ac Если abc.
При делении следует действовать тем же образом. (делим на положительное число знак сохраняется, делим на отрицательно число знак меняем)



Слайд 5 Свойства числовых неравенств.
Свойство 4. Если a>b и c>d,

Свойства числовых неравенств. Свойство 4. Если a>b и c>d, то a+c>b+d. Доказательство. Из

то a+c>b+d.
Доказательство. Из условия a-b – положительное число. c-d

–положительное число. Тогда сумма (a-b)+(c-d) тоже положительное число, поменяем местами некоторые слагаемые (a+с)-(b+d) от перемены мест слагаемых сумма не изменяется, значит (a+с)-(b+d) положительное число и a+c>b+d свойство доказано.
Свойство 5. Если a,b,c,d – положительные числа и a>b, c>d то ac>bd.
Доказательство. Так как a>b и c>0, то используя свойство 3 ac>bc. Так как c>d и b>0, то опять же используя свойство 3 cb>bd.
И так ac>bc и bc >bd, тогда используя свойство 1, получаем ac>bd как раз то, что требовалось доказать.
Определение. Неравенства вида a>b и c>d (a Неравенства вида a>b и cd) называются неравенствами противоположного смысла.
Тогда свойство 5 можно перефразировать, при умножение неравенств одного смысла у которых левые и правые части положительные получается неравенство того же смысла.



Слайд 6 Свойства числовых неравенств.
Свойство 6. Если a>b (a>0, b>0),

Свойства числовых неравенств. Свойство 6. Если a>b (a>0, b>0), то

то , где n –

любое натуральное число. То есть если обе части неравенства положительные числа, и их возвести в одну и туже натуральную степень, то получится неравенство того же смысла.
Так же заметим, если n нечетное число, то тогда для любых по знаку чисел a и b свойство 6 выполняется.
Свойство 7. Если a>b (a>0, b>0), то

Доказательство. Чтобы доказать данное свойство в разности
мы должны получить отрицательное число.




Мы знаем что a-b положительное число, и произведение двух положительных чисел тоже положительное число, т.е. ab>0. Тогда

- отрицательное число.

Свойство доказано.



Слайд 7 Свойства числовых неравенств.
Свойство 8. Если a>0, то тогда

Свойства числовых неравенств. Свойство 8. Если a>0, то тогда выполняется неравенство Доказательство. Рассмотрим

выполняется неравенство


Доказательство. Рассмотрим разность



Свойство доказано.
Свойство 9. Неравенство Коши. (Среднее

арифметическое больше либо равно среднего геометрического)
Если a и b неотрицательные числа, то выполняется неравенство


Доказательство. Рассмотрим разность



Свойство доказано.



Слайд 8 Свойства числовых неравенств.
Пример 1. Известно что -1.5

Свойства числовых неравенств. Пример 1. Известно что -1.5

и 3.1

Воспользуемся свойством 3, так как умножаем на положительное число то знак неравенства не меняется
-1.5·3-4.5<3a<6.3
б) Опять же используя свойство 3, умножая на отрицательное число следует менять знак неравенства
-2·3.1>-2·b>-2·5.3
-10.3<-2b<-6.2
в) Сложив неравенства одинаково смысла получим неравенство того же смысла
-1.5+3.11.6



Слайд 9 Свойства числовых неравенств.
г) Сначала умножим все части

Свойства числовых неравенств. г) Сначала умножим все части неравенства 3.1

неравенства 3.1

выполним операцию сложения
-1.5-5.3-6.8 д) Все части неравенства положительны, возведя их в квадрат получим неравенство того же смысла



е) Степень неравенства нечетная, тогда можно смело возводить в степень и не менять знак


ж) Воспользуемся свойством 7.



Слайд 10 Свойства числовых неравенств.
Пример 2. Сравните числа

а)

Свойства числовых неравенств. Пример 2. Сравните числа а) б) Решение. а) Возведем каждое

б)

Решение.
а) Возведем каждое из чисел в квадрат



Вычислим

разность квадратов этих квадратов


Очевидно, получили положительное число, что означает

Так как оба числа положительных, то


б)





  • Имя файла: prezentatsiya-svoystva-chislovyh-neravenstv-8-klass.pptx
  • Количество просмотров: 187
  • Количество скачиваний: 0
- Предыдущая Выступление на РМО для воспитателей на тему: Повышение качества речевого развития детей через повышение уровня речи педагога
Следующая - Классный руководитель – организатор деятельности учащихся, способствующий духовно-нравственному развитию их личности

Похожие презентации

Умножение многочленов Умножение многочленов 199
Комбинаторные задачи и их решения Комбинаторные задачи и их решения 167
Презентация по подготовке к ОГЭ и ЕГЭ Решение уравнений и систем уравнений с параметрами в среде Geogebra Презентация по подготовке к ОГЭ и ЕГЭ Решение уравнений и систем уравнений с параметрами в среде Geogebra 188
Решение текстовых задач ОГЭ по математике Решение текстовых задач ОГЭ по математике 265
График обратной пропорциональности График обратной пропорциональности 202
Квадратный корень Квадратный корень 154
Презентация по математике на тему: Применение показательной функции в природе, жизни и технике Презентация по математике на тему: Применение показательной функции в природе, жизни и технике 195
Сложение натуральных чисел и его свойства Сложение натуральных чисел и его свойства 170
Презентация урок математики В мире формул 7класс Презентация урок математики В мире формул 7класс 161
Презентация Математика сабағындағы топтық жұмыстың тиімділігі Презентация Математика сабағындағы топтық жұмыстың тиімділігі 244
Презентация для подготовки у ЕГЭ Первообразная. Задание 7. Презентация для подготовки у ЕГЭ Первообразная. Задание 7. 168
Обратные тригонометрические функции Обратные тригонометрические функции 190
: Линейная функция и ее графики 7 класс : Линейная функция и ее графики 7 класс 181
Тригонометрические уравнения Тригонометрические уравнения 239
Число. Имя числительное Число. Имя числительное 158
Как записывают и читают десятичные дроби Как записывают и читают десятичные дроби 179
Презентация по алгебре 8 класс на тему: Квадратные уравнения Презентация по алгебре 8 класс на тему: Квадратные уравнения 185
Презентация по алгебре: Системы рациональных неравенств (9 класс) Презентация по алгебре: Системы рациональных неравенств (9 класс) 202
Презентация 9 класс Геометрическая прогрессия Презентация 9 класс Геометрическая прогрессия 174
Презентация по математике на тему Сумма геометрической прогрессии Презентация по математике на тему Сумма геометрической прогрессии 255
Презентация внеаудиторного мероприятия Слабое звено в профессии Автомеханик Презентация внеаудиторного мероприятия Слабое звено в профессии Автомеханик 170
Построение диаграмм и графиков Построение диаграмм и графиков 137
Алгебраические дроби Сокращение дробей Алгебраические дроби Сокращение дробей 159
Задачи на делимость Задачи на делимость 242
Презентация по математике на тему Математика және мен 9 класс Презентация по математике на тему Математика және мен 9 класс 379
Решение неравенств (алгебра, 8 класс) Решение неравенств (алгебра, 8 класс) 151
Презентация к неделе математики в школе Шерлок Холмс Презентация к неделе математики в школе Шерлок Холмс 93
Игра Звездный час выпускника 9 класс Игра Звездный час выпускника 9 класс 181
Примеры решения логических задач Примеры решения логических задач 409
Виды соединений в комбинаторике Виды соединений в комбинаторике 203