Презентация на тему ычисление площадей плоских фигур с определенным интегралом

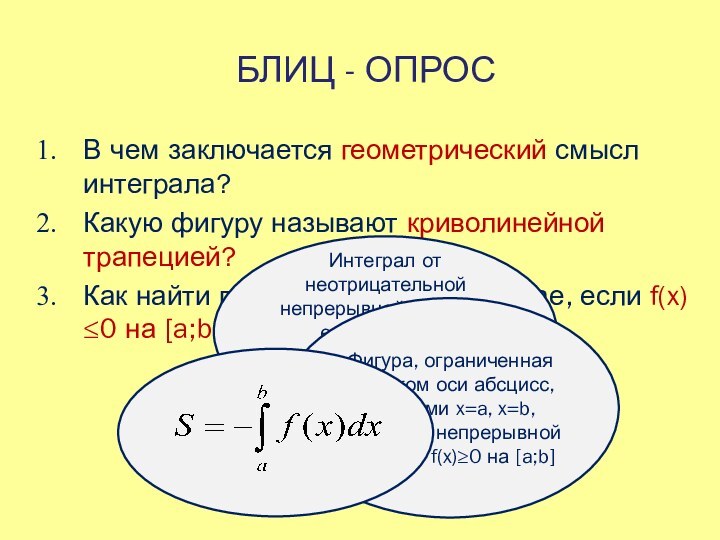
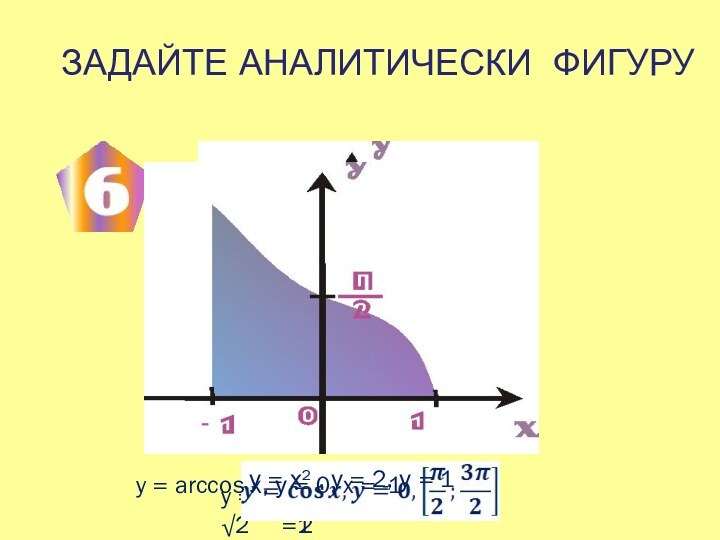
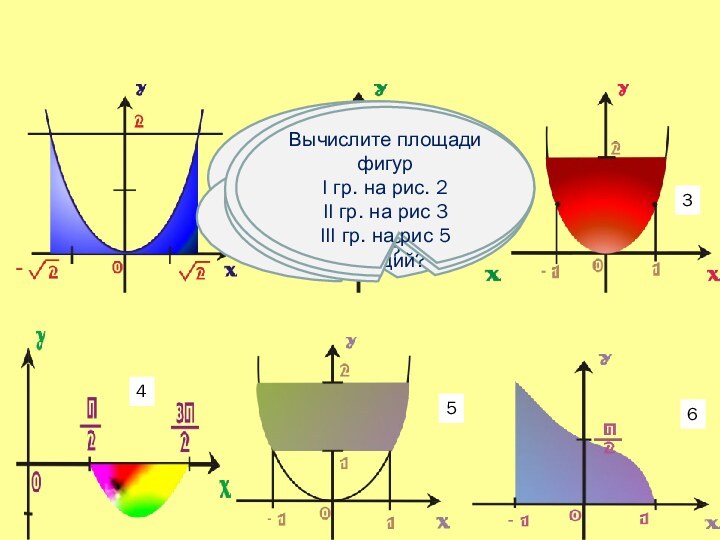
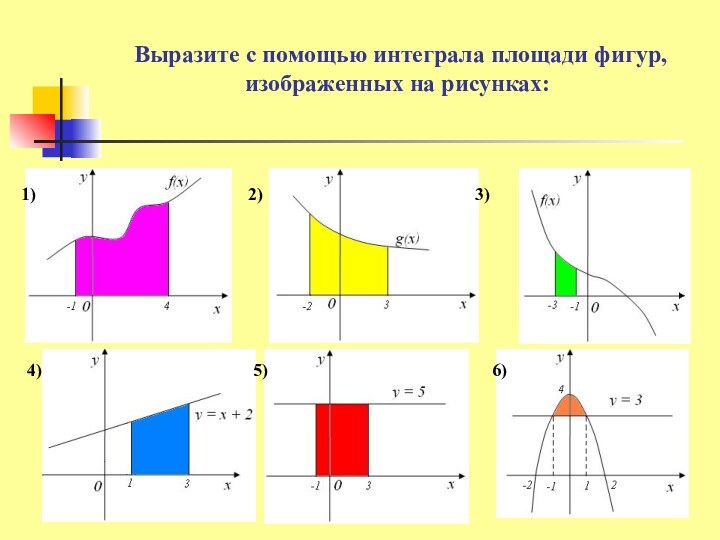
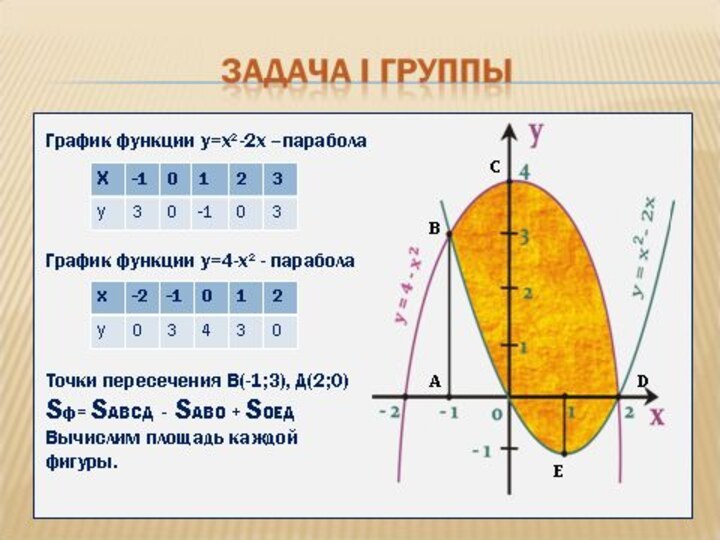
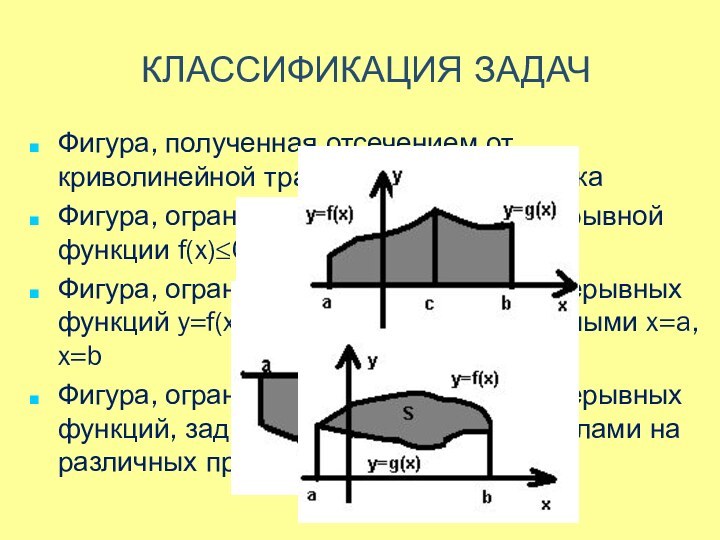
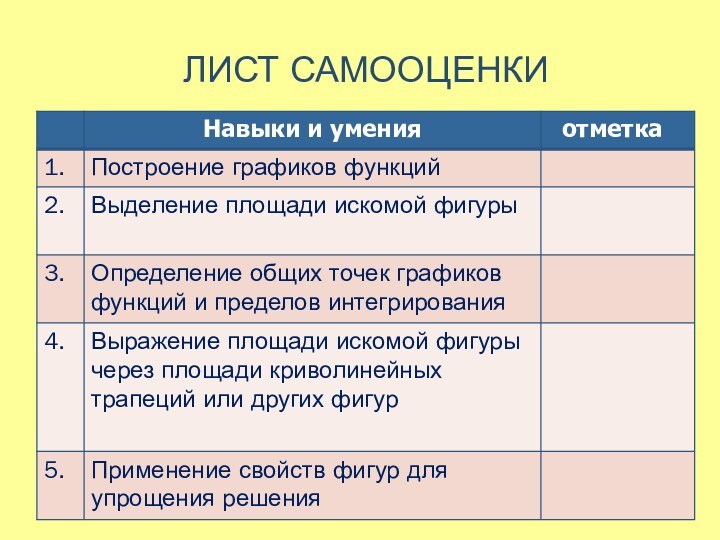
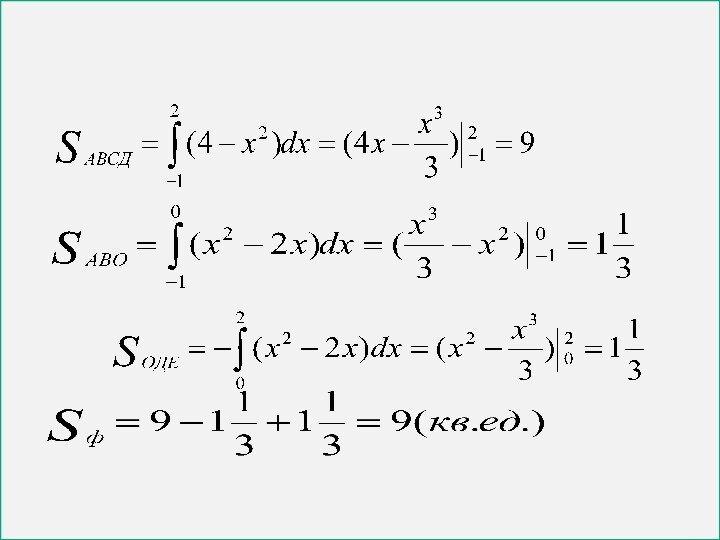на вычисление площадей фигур, в том числе фигур сложной

геометрической конфигурации,классифицировать задачи, систематизировать способы решения, скорретировать знания, познакомиться с историей развития интегрального исчисления;
- развивающая: научить мыслить и оперировать математическими знаниями, стимулировать мышление учащихся;
- воспитательная: развивать у учащихся коммуникативные компетенции (умение работать в группе, культуру общения), способствовать развитию интеллектуальной деятельности учащихся.

"

теоретических знаний
II. Практическое применение знаний
III. Защита домашних задач

IY. Постановка проблемы (обобщение)
Y. Коррекция знаний по теме
YI. Историческая справка
YII. Подведение итогов
YIII. Домашнее задание

фигуру называют криволинейной трапецией?
Как найти площадь фигуры в случае,

если f(x)≤0 на [a;b]?

Интеграл от неотрицательной непрерывной функции есть площадь соответствующей криволинейной трапеции

Фигура, ограниченная отрезком оси абсцисс, прямыми x=a, x=b, графиком непрерывной функции f(x)≥0 на [a;b]

х = -√2, х = √2
y = 2 -

х², у =1

у = х², у = 2

у = х² , у = 2, у = 1

y = arccos x, у = 0, x = -1

фигура на рис. 4 не является криволинейной трапецией?
Площадь каких

фигур можно найти как разность площадей криволинейных трапеций?

Площадь какой фигуры можно найти без помощи интеграла?

Вычислите площади фигур
I гр. на рис. 2
II гр. на рис 3
III гр. на рис 5

на рисунках:
1)
2)
3)
4)
5)
6)

у=½ х² -парабола



У=2х – прямая



Sф = SОАЕ+SЕАВ =
(SОАД -

SОЕД) +(S ДАВС – SДЕВС)

E

SDMN + SMNF =
= SABCD – SABD + SDCM

+ SDMN + SMNFK - SMKF

площадь фигуры, не являющейся криволинейной трапецией?



Задачи на вычисление площадей

фигур с помощью интеграла можно классифицировать по виду геометрических фигур, площади которых необходимо вычислить

Решение проблемы

ограниченная графиком непрерывной функции f(x)≤0 на [a;b]
Фигура, ограниченная графиками

непрерывных функций y=f(x), y=g(x), f(x)≥g(x) ≥0 и прямыми x=a, x=b
Фигура, ограниченная графиками непрерывных функций, заданных различными формулами на различных промежутках

вдоль оси Оу)
Применение свойств интеграла (свойство аддитивности)
Свойство симметрии фигуры

ограниченной линиями

y = x, y = 5 – x, x = 1, x = 2.

x

y

0

1

2

5

5

y = x

y = 5 - x

A

B

C

D

integro
«целый» от латинского integer


от латинского
primitivus – начальный,
ввел

Жозеф Луи Лагранж
(1797г.)

«Примитивная функция»,

Архимедом, и использовался для расчёта площадей парабол и приближенного

расчёта площади круга.

Евдокс Книдский

Архимед

Первым известным методом для расчёта интегралов является метод исчерпания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен.

содержится в
«Методе флюксий...»
(1670–1671, опубликовано в 1736).
Переменные

величины - флюенты(первообразная или неопределенный интеграл)

Скорость изменения флюент – флюксии (производная)

XVII века
Символ образовался из буквы
S — сокращения слова
 summa

(сумма)

несмотря на то, что в математике его времени не

было понятия интеграла
Но лишь интегральное исчисление дает общий метод решения всех подобных задач
Недаром даже поэты воспевали интеграл

Что сделали

Что планировали

Обобщить знания по теме «Вычисление площадей плоских фигур с помощью определённого интеграла»

1.Классифицировали задачи
2.Систематизировали способы решения
3.Скорректировали знания
4.Совершили экскурс в историю
5. Подготовились к контрольной работе по данной теме.