Слайд 2
Общие сведения
Одним из принципов TQM является
то, что в основе принятия решений должны быть только
факты, а не интуиция.
Главные причины трудностей, возникающих при управлении качеством, — ложные представления и ошибочные действия. Что ложно, а что ошибочно, можно различить организовав процесс поиска фактов, т.е. статистического материала.
Слайд 3
Польза статистических данных
Сам по себе статистический
материал, без обработки и анализа, не позволяет решить возникшую
проблему.
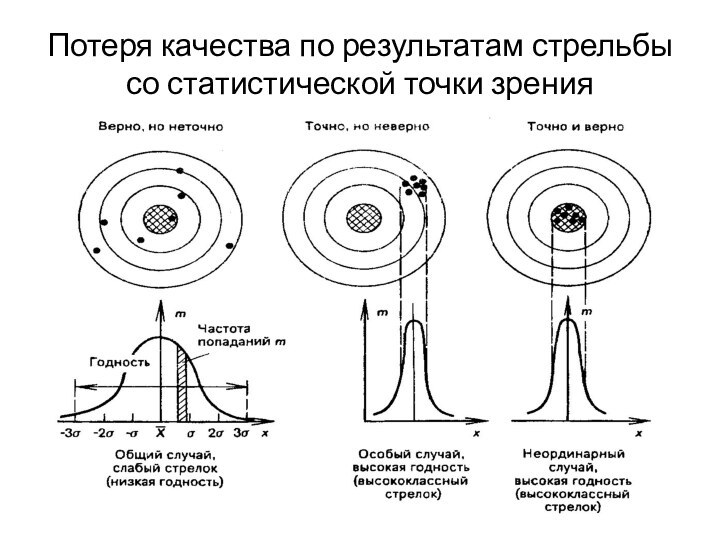
Понятие статистического материала можно проиллюстрировать результатами стрельбы по мишени (рис. 1). Р.3.1
Слайд 4
Потеря качества по результатам стрельбы
со статистической точки
зрения
Слайд 5
Случай 1
1) все пули попали в мишень, что
соответствует «годности» всех семи произведенных выстрелов, но их разброс
очень велик, что говорит о плохой подготовке стрелка (хотя все попадания лежат «в пределах допуска» – внешней окружности мишени).
Слайд 6
Случай 2
Во втором и в третьем
случаях все семь выстрелов проведены точно (при отсутствии разброса),
но:
2) все пули кучно попали в мишень, но не в центр – здесь можно говорить о потерях качества стрельбы (не за счет умения стрелка, а за счет качества оружия, например, систематической погрешности оружия - м. б. из-за сбитого прицела);
Слайд 7
Случай 3
3) если все пули стрелка
попадают в центр мишени, соответствующий, например, 10 очкам (номинал),
то он набирает максимум очков и его потери на качество стрельбы равны нулю.
Пример иллюстрирует смысл функции потерь качества (по Тагучи)
Слайд 8
Инструменты контроля качества
Современные статистические методы сложны
для восприятия и широкого применения всеми участниками процесса.
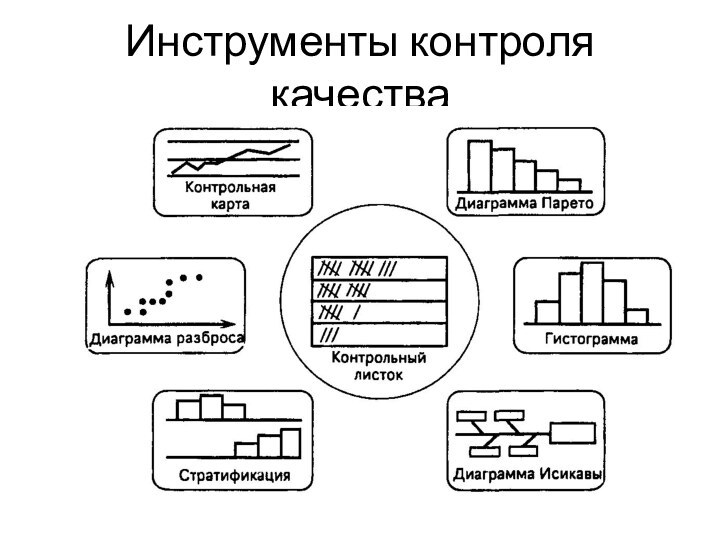
Японские ученые отобрали семь простых, наглядных, визуализируемых методов (рис. 2), которые можно понять, эффективно использовать (без специальной математической подготовки) и превратили их в эффективные инструменты контроля качества (заслуга профессора Исикавы и др.),
Слайд 9
Достоинства ИКК
Несмотря на простоту, инструменты контроля
качества (ИКК) позволяют сохранить связь со статистикой и дают
возможность профессионалам пользоваться результатами этих методов и при необходимости совершенствовать их.
Слайд 10
Семь инструментов контроля качества (рис. 3):
- контрольный листок,
-
гистограмма,
- диаграмма разброса,
- диаграмма Парето,
- стратификация (расслоение),
- диаграмма Исикавы
(причинно-следственная диаграмма),
- контрольная карта.
ИКК можно рассматривать и применять как отдельные инструменты, так и как систему методов (разную в различных обстоятельствах).
Слайд 12
Необходимость и достаточность ИКК
Семь инструментов контроля
качества являются необходимыми и достаточными статистическими методами, применение которых
(по мнению Исикавы), помогает решить 95 % всех проблем, возникающих при контроле качества (КК) на производстве.
Слайд 13
ИКК для познания, а не управления
Статистические
методы — это то средство, которое необходимо изучать, чтобы
внедрить управление качеством. Они — наиболее важная составляющая комплексной системы контроля Всеобщего Управления Качеством (TQM).
Семь простых статистических методов контроля качества - это инструменты познания, а не инструменты управления.
Слайд 14
Назначение ИКК —
— контроль протекающего процесса и предоставление
участнику процесса фактов для корректировки и улучшения процесса, что
лежит в основе одного из важнейших требований TQM — постоянного самоконтроля.
Статистические методы ИКК применяются в производстве, в планировании, проектировании, маркетинге, материально-техническом снабжении и т.д.
Слайд 15
Применение статистических методов —
- действенный путь разработки новых
технологий и контроля качества процессов. Многие ведущие фирмы стремятся
к их активному использованию, а некоторые тратят более ста часов ежегодно на обучение этим методам своих сотрудников, осуществляемое в рамках самой фирмы.
Слайд 16
Знать, уметь, хотеть работать и учиться
Хотя
знание статистических методов — часть нормального образования инженера, само
знание еще не означает умения применить его.
Способность рассматривать события с точки зрения статистики важнее, чем знание самих методов.
Слайд 18
Что с ними делать?
Руководством к действиям
служат данные, из которых мы узнаем о фактах и
принимаем соответствующие меры.
Прежде чем начать собирать данные, надо заранее решить, что с ними делать.
Слайд 19
Любые собираемые данные
имеют свое назначение, и после того,
как информация собрана, нужно начать с нею работать.
Когда цель сбора данных установлена, она становится основой:
- для определения характера сравнений, которые надлежит произвести,
- типа данных, которые нужно собрать.
Слайд 20
Цели сбора данных
в процессе контроля качества состоят в
следующем:
- контроль и регулирование процесса;
- анализ отклонений
от установленных требований;
- контроль выхода процесса.
Слайд 21
Например,
возник вопрос о вариации в показателе качества изделия.
Если производить только один замер в день,
то нельзя судить о вариациях в течение дня.
Если вы хотите понять, каким образом два разных работника допускают дефекты, то надо брать раздельные выборки, чтобы можно было сравнить работу каждого из них.
Слайд 22
Таблица 1. Пример формы регистрации данных
Слайд 23
Расслоение, или стратификация
Если сравнение выявляет явные
различия, то меры по их устранению также будут способствовать
уменьшению изменчивости процесса.
Подобное разделение группы данных на несколько подгрупп по определенному признаку называется расслоением, или стратификацией. Она чрезвычайно важна и должна применяться во всех случаях.
Слайд 24
Упорядочение
Для их анализа собранных данных используются различные
статистические методы, предназначенные для превращения данных в источник информации.
Важно в процессе сбора тщательно упорядочить данные, чтобы облегчить их последующую обработку.
Слайд 25
Во-первых,
надо четко зарегистрировать источник данных (без такой регистрации
данные окажутся мертвыми). Часто, несмотря на заметные затраты ресурсов
на сбор данных о показателях качества, из них можно извлечь мало полезной информации, поскольку не зафиксированы существенные сведения (например: день недели, когда собирались данные; оборудование, на котором производилась работа; рабочий, делавший операцию; партия используемых материалов и т.д.
Слайд 26
Во-вторых,
данные надо регистрировать таким образом, чтобы их было
легко использовать.
Поскольку данные часто применяются для
вычисления статистических характеристик (средние значения, разброс, размах и проч.), то лучше их записывать так, чтобы облегчить эти вычисления.
Если данные требуется собирать постоянно, то надо заранее разработать стандартные формы регистрации данных, что делается для контрольных листков (см. ниже).
Слайд 27
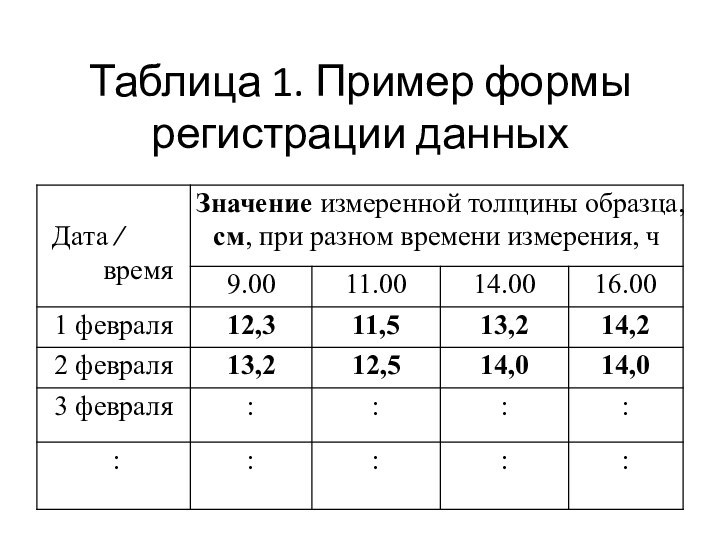
Например,
данные измерений толщины образцов, проводимые четыре раза в
день в течение 25 дней, удобно регистрировать в форме,
показанной в табл. 1 (выше).
В этом случае:
- ежедневные подсчеты можно производить по строкам,
- подсчеты для соответствующих часов — по столбцам.
Слайд 28
Статистический ряд и его характеристики
Слайд 29
Выборка и генеральная совокупность
Сбор и обработка
статистических данных базируются на применении так называемого выборочного метода.
Выборкой называют часть данных, полученных из общей совокупности, называемой генеральной совокупностью, по отношению к которой на основании данных выборки делают соответствующие выводы.
Слайд 30
Представительность и репрезентативность
Генеральная совокупностью подразумевает однородную
совокупность данных, по которой делаются выводы при принятии решения
на основании результатов анализа выборки.
Если выборка достаточно хорошо представляет соответствующие характеристики генеральной совокупности, то такую выборку называют представительной или репрезентативной.
Слайд 31
Не цель, а средство
Для управления процессом
мы стремимся на основе собранных данных выявить факты, а
затем, опираясь на эти факты, предпринять необходимые действия.
Сбор данных — не самоцель, а средство отыскания тех фактов, которые стоят за данными.
Слайд 32
Не цель, а средство
Проводим выборочное обследование
продукции.
Для этого:
- берем некоторую выборку,
- проводим на ней измерения,
- решаем, стоит ли принимать всю партию как годную или нет.
Здесь наше внимание сосредоточивается не на самой выборке, а на качестве всей партии.
Слайд 33
Пример 3
— управление процессом с помощью контрольной карты.
Здесь наша цель заключается не в определении
характеристики выборки, взятой для нанесения на карту, а в выяснении состояния самого процесса.
Слайд 34
В приведенных примерах
генеральной совокупностью являются:
1) — исследуемые параметры
качества сдаваемой продукции,
2) — параметры качества процесса.
Сбор
и регистрация данных на первый взгляд кажутся легким делом, но на самом деле это довольно сложно.
Слайд 35
Пример 4. Попробуйте
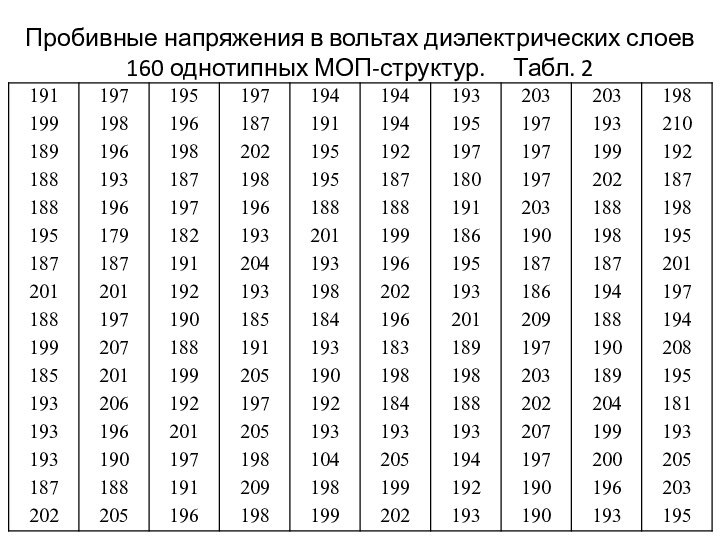
В табл. 2
приведены результаты измерений пробивного напряжения диэлектрических слоев 160 однотипных
МОП-структур, зафиксированных в порядке поступления на измерительную установку.
Попробуйте, засекая время, быстро определить:
- наибольшее и наименьшее значения пробивного напряжения;
- сколько раз то или иное значение повторяется.
Слайд 36
Пробивные напряжения в вольтах диэлектрических слоев 160 однотипных
МОП-структур. Табл. 2
Слайд 37
Ранжирование —
— непростая задача, требующая времени, внимания
и аккуратности исполнителя.
Значительно проще можно решить
эту задачу, если данные, приведенные в табл. 2, расположить в возрастающем или убывающем порядке.
Упорядоченное представление данных (здесь - по возрастанию или убыванию) называют ранжированным.
Слайд 38
Статистический ряд
Для получения статистического ряда необходимо
не только ранжировать статистический материал, приведенный в табл. *3.2,
но и подвергнуть его дополнительной обработке, объединив одни и те же значения пробивного напряжения в группы.
Слайд 39
Случайная величина
Выборочные данные являются случайными, так
как невозможно предсказать точные их значения до проведения измерений.
Поэтому измеряемую величину называют случайной величиной.
Слайд 40
Частота, вес
Число случаев в группе для
каждого из повторяющихся значений (т1, т2, т3, … тk)
называют абсолютной частотой или статистическим весом этого значения случайной величины.
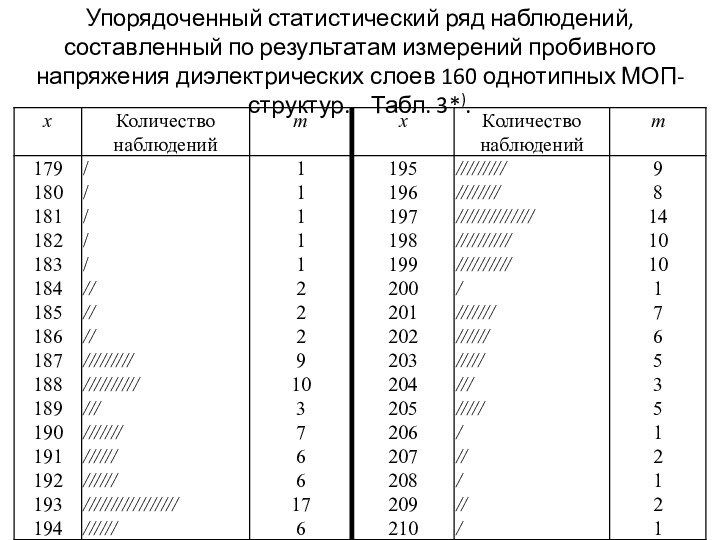
Полученный после обработки данных табл. 2 статистический ряд приведен в табл. 3.
Слайд 41
Упорядоченный статистический ряд наблюдений, составленный по результатам измерений
пробивного напряжения диэлектрических слоев 160 однотипных МОП-структур. Табл.
3*).
Слайд 42
*)Примечание к табл. 3
Контрольный
листок для регистрации несоответствий, например, дефектов (см. л.1).
Порядок заполнения: каждый раз, когда работающий или контролер обнаруживает дефект, он делает пометку (штрих - /) на бланке.
На том же бланке в конце указанного времени регистрации (например, рабочего дня) фиксируются итоговые данные по количеству каждого типа дефектов.
Слайд 43
Наглядность
Числа, стоящие в столбце х, называют
упорядоченным рядом случайной величины, а числа, стоящие в столбце
т, — рядом частот.
Таблица 3 дает более наглядную картину, чем таблица 2 — видно, что:
- структуры с пробивным напряжением от 190 до 199 В встречаются чаще других;
- структуры с пробивным напряжением меньше 179 и больше 210 В вообще не встречаются.
Слайд 44
Различие законов распределения дискретных и непрерывных величин
Изменение фиксируемых значений случайной величины бывает дискретным или непрерывным,
что принципиально:
- дискретное распределение описывается обычно гипергеометрическим, биноминальным или пуассоновским и иными законами;
- непрерывная величина описывается законом Гаусса, Вейбулла и др.
Слайд 45
Дискретным
изменением случайной величины называют такое, при
котором рядом лежащие значения в ранжированном ряду отличаются одно
от другого на некоторую конечную величину (обычно целое число).
Например, когда число дефектных изделий может быть только целым.
Слайд 46
Пример —
— число дефектных изделий в
выборках, которые периодически берутся из постоянно текущего технологического процесса.
Здесь число дефектных изделий может быть только целым.
Слайд 47
Непрерывным
изменением случайной величины называют такое, при
котором рядом лежащие его значения в ранжированном ряду отличаются
одно от другого на сколь угодно малую величину.
Слайд 48
Примером непрерывного изменения
случайной величины служит изменение
пробивного напряжения (табл.2 выше).
Например, зафиксирован результат измерения
197 В, но пробивное напряжение на диэлектрике обследуемой структуры не обязательно точно равно этому числу. Если применять более точный измерительный прибор, то результат может оказаться иным, например, 196,86 или 197,32 В и проч.
Если у 14 структур зафиксировано пробивное напряжение 197 В, то значение каждого из них колеблется от 166,5 до 197,4 В.
Слайд 49
Интервал, класс
При непрерывном изменении случайной величины
ее распределение называют интервальным.
За величину интервала, или
класса, как правило, принимают его центральное значение, т.е. середину.
Слайд 50
Правило 1
Если значение случайной величины находится
точно на границе двух классов, то условно можно считают
данное значение принадлежащим к обоим классам и прибавлять одну его половину к верхнему, а другую — к нижнему классу.
Слайд 51
Правило 2
Другое правило - в каждый
класс включаются те наблюдения, числовые значения которых:
- больше нижней
границы класса;
- меньше или равны верхней границе класса.
Слайд 52
Число классов,
на которые следует группировать статистический
материал:
- не должно быть слишком большим (тогда ряд
распределения становится невыразительным и частоты в нем обнаруживают незакономерные колебания);
- не должно быть слишком малым (тогда свойства распределения описываются статистическим рядом слишком грубо).
При большом числе наблюдений рационально выбирать 10…20 классов.
Слайд 53
Ширина классов (длина интервалов)
может быть:
- одинаковой
(что проще);
- различной.
Если брать ее одинаковой, то ширина
класса подсчитывается по формуле
(1)
где хi , хi+1 — границы i-го класса;
хmax , хmin — максимальное и минимальное значения случайной величины в ранжированном ряду;
k — число классов.
Слайд 54
Формирование данных
При формировании данных о случайных
величинах, распределенных неравномерно, удобно выбирать в области наибольшей плотности
распределения ширину классов более узкую, чем в области малой плотности.
Слайд 55
В случае неодинаковой ширины классов
удобнее пользоваться не абсолютной величиной mi , а относительной,
равной отношению частоты mi , приходящейся на i-й класс или i-е значение параметра, к общему числу наблюдений n:
wi = тi /n (2)
Относительную величину wi называют относительной частотой или частостью.
Сумма частостей всех интервалов равна единице, или 100 %.
Слайд 56
К примеру табл.3 (нч)
Если заранее подготовить
бланки в виде табл. 3 (см. выше) и, производя
измерения, вести ее заполнение, заранее выбрав классы (интервалы), то легко узнать состояние производства и качество произведенных за день изделий.
Приведенное в табл. 3 распределение пробивного напряжения имеет 32 интервала, каждый из которых равен 1 В.
Слайд 57
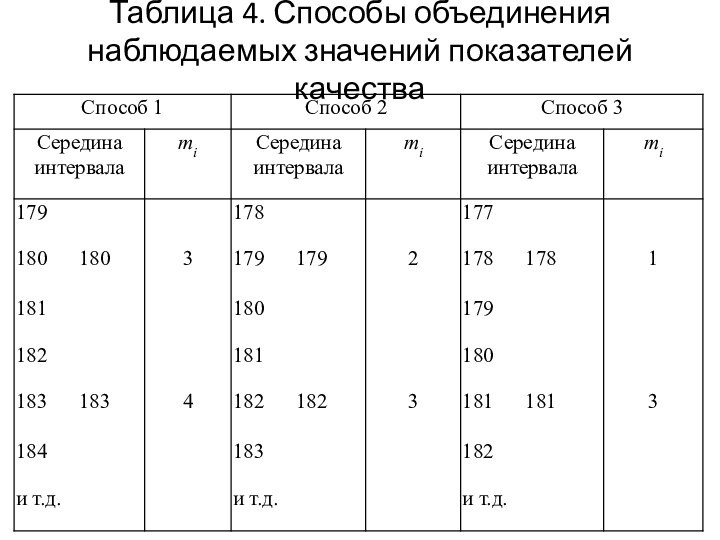
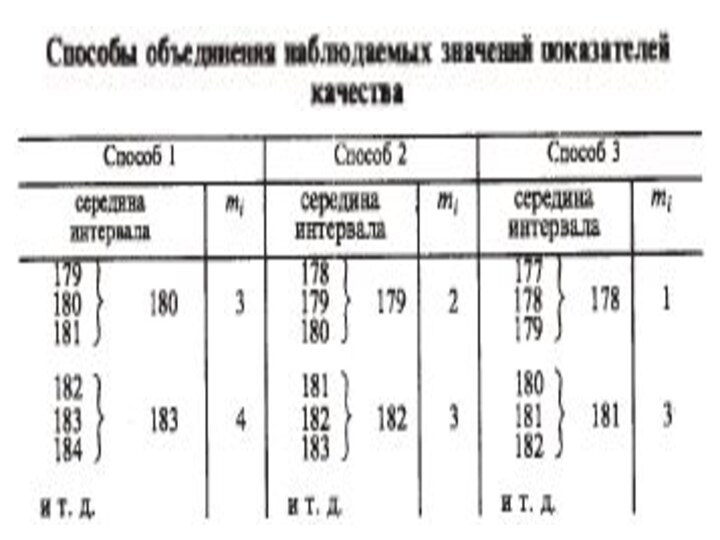
К примеру табл.3 (пр)
Числа интервалов (классов)
в табл. 3 необходимо значительно уменьшить: объединим по три
значения показателя качества так, чтобы получились классы шириной 3 В.
Способы такого объединения показаны в табл. 4.
При втором и третьем способах (см. табл. 3) к числу 179 подключается соответственно еще одно или два значения, не зафиксированных в процессе измерений.
Слайд 58
Таблица 4. Способы объединения наблюдаемых значений показателей качества
Слайд 60
Способы объединения наблюдаемых значений показателей качества
Эти
значения при измерении пробивного напряжения 160 структур не наблюдались,
поэтому их частоты равны нулю.
То же самое справедливо для числа 210, замыкающего упорядоченный ряд.
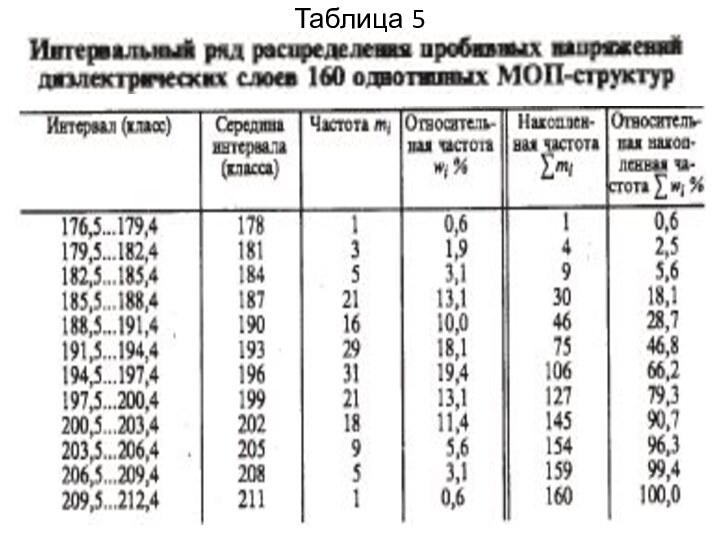
Если воспользоваться третьим способом, то получим интервальный ряд распределения с числом классов k = 12 и шириной класса, равной 2,9 В (приведен в табл. 5 ниже).
Слайд 62
Вспомнить основные определения теории вероятностей и статистики
Удобно представлять статистический материал числовыми значениями, которые отражают существенные
характеристики статистического ряда — характеристики положения и рассеивания случайной величины (см. понятия: математическое ожидание, дисперсия, законы распределения и проч., и проч., кратко перечисленные ранее).